山东省泰安市岱岳区2021年中考数学三模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 2021的倒数的相反数是( ).A、 B、 C、 D、20212. 下列运算正确的是( ).A、 B、 C、 D、3. 0.00007用科学记数法表示为 ,则( )A、 , B、 , C、 , D、 ,4. 下面图形是用数学家名字命名的,其中是中心对称图形但不是轴对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
5. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 , .若 , ,则 的度数是( ).
斐波那契螺旋线
5. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 , .若 , ,则 的度数是( ). A、50° B、60° C、65° D、70°6. 小冉准备完成课后作业,却发现某个题目中有一个数据被墨迹覆盖:已知一组数据32,20,22,30,
A、50° B、60° C、65° D、70°6. 小冉准备完成课后作业,却发现某个题目中有一个数据被墨迹覆盖:已知一组数据32,20,22,30, ,36,则这组数据的平均数是______,众数是______.小冉的妈妈翻看答案后告诉小冉,这组数据的平均数是27.则被墨迹覆盖的数据和这组数据的众数分别是( ). A、20,20 B、22,22 C、24,24 D、30,307. 如图, 是圆O的直径,C,D是弧 上的两点,连接 , 相交于点E,若 ,那么 的度数为( )
,36,则这组数据的平均数是______,众数是______.小冉的妈妈翻看答案后告诉小冉,这组数据的平均数是27.则被墨迹覆盖的数据和这组数据的众数分别是( ). A、20,20 B、22,22 C、24,24 D、30,307. 如图, 是圆O的直径,C,D是弧 上的两点,连接 , 相交于点E,若 ,那么 的度数为( )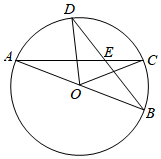 A、 B、 C、 D、8. 把方程 x2﹣x﹣5=0,化成(x+m)2=n的形式得( )A、(x﹣ )2= B、(x﹣ )2= C、(x﹣ )2= D、(x﹣ )2=9. 如图,经过A、C两点的⊙O与△ABC的边BC相切,与边AB交于点D,若∠ADC=105°,BC=CD=3,则AD的值为( )
A、 B、 C、 D、8. 把方程 x2﹣x﹣5=0,化成(x+m)2=n的形式得( )A、(x﹣ )2= B、(x﹣ )2= C、(x﹣ )2= D、(x﹣ )2=9. 如图,经过A、C两点的⊙O与△ABC的边BC相切,与边AB交于点D,若∠ADC=105°,BC=CD=3,则AD的值为( ) A、3 B、2 C、 D、10. 如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3= 的图象在同一直角坐标系中,若y3>y2>y1 , 则自变量x的取值范围是( )
A、3 B、2 C、 D、10. 如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3= 的图象在同一直角坐标系中,若y3>y2>y1 , 则自变量x的取值范围是( )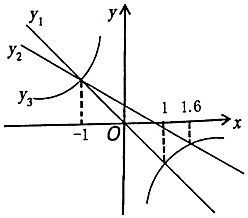 A、x<﹣1 B、﹣1<x<0或x>1.6 C、﹣1<x<0 D、x<﹣1或0<x<111. 如图,正方形 和正方形 的顶点 在同一直线 上,且 ,给出下列结论: , , 的面积 ,其中正确的个数为( )
A、x<﹣1 B、﹣1<x<0或x>1.6 C、﹣1<x<0 D、x<﹣1或0<x<111. 如图,正方形 和正方形 的顶点 在同一直线 上,且 ,给出下列结论: , , 的面积 ,其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个12. 如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列: , , , , , , , ……,则 的值为( )
A、1个 B、2个 C、3个 D、4个12. 如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列: , , , , , , , ……,则 的值为( ) A、1275 B、1326 C、1378 D、1431
A、1275 B、1326 C、1378 D、1431二、填空题
-
13. .14. 《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为.15. △ABC中,∠ABC=30°,AB=4 ,AC=4,则BC= .16. 如图,矩形ABCD中,AB= ,将矩形ABCD绕点A逆时针旋转45°得到矩形AB′C′D′,此时点B′恰好落在CD上时,点C的运动路径为弧CC′,则图中阴影部分的面积为 .
 17. 二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q( ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣ 或﹣ .其中正确的有 . (请将正确结论的序号全部填在横线上)
17. 二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q( ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣ 或﹣ .其中正确的有 . (请将正确结论的序号全部填在横线上)
18. 在一条笔直的路边 上建一个燃气站,向 同侧的 、 两个城镇分别铺设管道输送燃气.其中 、 之间规划位置固定的生态保护区,其中 在 的正东方向, ,四边形 为边长是3的正方形.现要求燃气管道不能穿过该区域,试确定燃气站的位置使铺设管道的路线最短,则最短路程为 .
三、解答题
-
19. 先化简,再求值:(1+ ) ,其中x是不等式组 的整数解.20. 2015年2月27日,在中央全面深化改革领导小组第十次会议上,审议通过了《中国足球改革总体方案》,体制改革、联赛改革、校园足球等成为改革的亮点.在联赛方面,作为国内最高水平的联赛﹣﹣中国足球超级联赛今年已经进入第12个年头,中超联赛已经引起了世界的关注.图9是某一年截止倒数第二轮比赛各队的积分统计图.
 (1)、根据图,请计算该年有支中超球队参赛;(2)、补全图一中的条形统计图;(3)、根据足球比赛规则,胜一场得3分,平一场得1分,负一场得0分,最后得分最高者为冠军.倒数第二轮比赛后积分位于前4名的分别是A队49分,B队49分,C队48分,D队45分.在最后一轮的比赛中,他们分别和第4名以后的球队进行比赛,已知在已经结束的一场比赛中,A队和对手打平.请用列表或者画树状图的方法,计算C队夺得冠军的概率是多少?21. 如图,直线 分别与x轴,y轴相交于A , B , 与反比例函数y= 的图象相交于点 ,作 轴于C , 已知△APC的面积为9.
(1)、根据图,请计算该年有支中超球队参赛;(2)、补全图一中的条形统计图;(3)、根据足球比赛规则,胜一场得3分,平一场得1分,负一场得0分,最后得分最高者为冠军.倒数第二轮比赛后积分位于前4名的分别是A队49分,B队49分,C队48分,D队45分.在最后一轮的比赛中,他们分别和第4名以后的球队进行比赛,已知在已经结束的一场比赛中,A队和对手打平.请用列表或者画树状图的方法,计算C队夺得冠军的概率是多少?21. 如图,直线 分别与x轴,y轴相交于A , B , 与反比例函数y= 的图象相交于点 ,作 轴于C , 已知△APC的面积为9. (1)、请分别求出直线l与反比例函数 的表达式;(2)、将直线l上下平移,平移后的直线与x轴相交于点D , 与反比例函数 的图象交于点Q , 作 轴于E , 如果 的面积是 的面积的2倍,求点D的坐标.22. 某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如表:
(1)、请分别求出直线l与反比例函数 的表达式;(2)、将直线l上下平移,平移后的直线与x轴相交于点D , 与反比例函数 的图象交于点Q , 作 轴于E , 如果 的面积是 的面积的2倍,求点D的坐标.22. 某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如表:批发价(元)
零售价(元)
黑色文化衫
10
25
白色文化衫
8
20
(1)、若学校恰好用完预计进货款1240元,则应购进黑白两种文化衫各多少件?(2)、若学校规定黑色文化衫的进货量不超过白色文化衫进货量的3倍,应怎样进货才能使学校在销售完这两种文化衫时获得的利润最多?利润最多为多少元?23. 如图①,点 是菱形 对角线 上的一点,点 在 的延长线上,且PE=PB. (1)、求证: ;(2)、如图②,当 时,连接 ,则 是否为定值?如果是,请求其值;如果不是,请说明理由.24. 如图,在平面直角坐标系中,直线 与 轴相交于点 ,与 轴相交于点 ,抛物线 经过 、 两点.
(1)、求证: ;(2)、如图②,当 时,连接 ,则 是否为定值?如果是,请求其值;如果不是,请说明理由.24. 如图,在平面直角坐标系中,直线 与 轴相交于点 ,与 轴相交于点 ,抛物线 经过 、 两点. (1)、求这条抛物线的解析式;(2)、设抛物线与 轴的另一个交点为 ,点 是抛物线上一点,点 是直线 上的一点,当四边形 是平行四边形时,求点 的坐标;(3)、在(2)的条件下,连接 ,在 的内部作射线 与抛物线的对称轴相交于点 ,且使得 ,请你直接写出线段 的长度.25. 如图
(1)、求这条抛物线的解析式;(2)、设抛物线与 轴的另一个交点为 ,点 是抛物线上一点,点 是直线 上的一点,当四边形 是平行四边形时,求点 的坐标;(3)、在(2)的条件下,连接 ,在 的内部作射线 与抛物线的对称轴相交于点 ,且使得 ,请你直接写出线段 的长度.25. 如图 (1)、如图①, ,求证: .(2)、(尝试应用)
(1)、如图①, ,求证: .(2)、(尝试应用)如图②,在菱形 中, ,点E , F分别为边 上两点,将菱形 沿 翻折,点A恰好落在对角线 上的点P处,若 ,求 的值.
(3)、(拓展提高)如图③,在矩形 中,点P是 边上一点,连接 ,若 ,求 的长.