陕西省初中数学历年真题与模拟汇编：图形2
试卷更新日期：2021-07-07 类型：二轮复习
一、单选题
-
1. 如图， ，若 ，则 （ ）
A、 B、 C、 D、2. 如图，在 中， ，若 为劣弧 上的一点， ，则 的度数为（ ）
A、 B、 C、 D、3. 如图，直线l1 l2 ， ∠1＝50°，∠2＝23°20′，则∠3的度数为（ ）
A、26°40′ B、27°20′ C、27°40′ D、73°20′4. 如图，已知AB∥CD，∠1＝125°，∠2＝55°，则∠C＝（ ）
A、45° B、50° C、70° D、65°5. 如图，直线 ， ， ，那么 的度数是（ ）
A、 B、 C、 D、6. 如图，将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起，其中点A′与点A重合，点C′落在边AB上，连接B′C．若∠ACB=∠AC′B′=90°，AC=BC=3，则B′C的长为（ ）
A、3 B、6 C、3 D、7. 如图，在矩形ABCD中，AB=2，BC=3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（ ）
A、 B、 C、 D、8. 如图，点A，D，B，C是圆O上的四个点，连接AB，CD，相交于点E，若∠BOD＝40°，∠AOC＝120°，则∠AEC等于（ ）
A、70° B、75° C、80° D、85°9. 如图，菱形 对角线 ， 交于点 ， ，过点 作 交 的延长线于点 .若菱形 的面积为4，则菱形的边长为（ ）
A、 B、2 C、 D、410. 如图，点E是矩形ABCD的边CD上一点，作AF⊥BE于F，连接DF，若AB＝6，DF＝BC，则CE的长度为（ ）
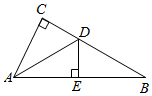
A、2 B、 C、3 D、11. 如图，已知 中，CD⊥AB，垂足为D，CE平分∠ACD交AD于E，若CD＝12，BC＝13，且 的面积为48，则点E到AC的距离为（ ）
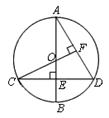
A、5 B、3 C、4 D、112. 如图，AB是⊙O的直径，弦CD⊥AB，DE∥CB交⊙O于点E，若∠CBA＝20°，则∠AOE的度数为（ ）
A、120° B、80° C、110° D、100°13. 如图，在⊙O中，点A、B、C均在圆上，连接OA，OB，OC，BC，AC，若AC OB，OC＝4，AB＝5，则BC＝（ ）
A、5 B、 C、 D、814. 如图，AB是⊙O的直径，弦CD交AB于点E，且AE＝CD＝16，∠BAC＝ ∠BOD，则⊙O的半径为（ ）
A、4 B、8 C、10 D、615. 如图，矩形 中， ，点 在边 上， 平分 ， ，则 长（ ）
A、 B、 C、 D、216. 如图，在 中， 是 的角平分线， 于点 ， ， ， ，则 长是（ ）
A、1 B、 C、 D、217. 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD＝120°，AB＝AD＝6，则⊙O的半径长为（ ）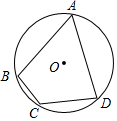
A、 B、 C、 D、3二、填空题
-
18. 如图， 中， ， ， .以 为边作正方形 .点M是边 上一动点，连接 ，过O作 的垂线，垂足为N，连接 .则线段 的最小值是.
19. 如图，A、B、C、D为一个外角为40°的正多边形的顶点，若O为正多边形的中心，则∠OAD＝°.
20. 如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC．若AC=6，则四边形ABCD的面积为 ．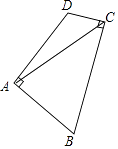
三、解答题
-
21. 如图，△ABC中，点D、E在边BC上，∠ADC＝∠AEB，CD＝BE.求证：∠BAD＝∠CAE.
22.如图，在▱ABCD中，连接BD，在BD的延长线上取一点E，在DB的延长线上取一点F，使BF=DE，连接AF、CE．
求证：AF∥CE．
23. 如图，在▱ABCD中，点E，F是对角线AC上的两点，且AF=CE，连接DE，BF.求证：DE∥BF.
24. 如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M，N，垂足为点O.求证：BM＝DN.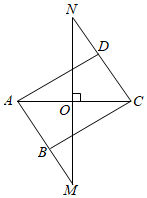
25. 如图，四边形ABCD中，AB DC，AC平分∠BAD，CE DA交AB于点E.求证：四边形ADCE是菱形.
四、作图题
-
26. 如图，在钝角△ABC中，过钝角顶点B作BD⊥BC交AC于点D．请用尺规作图法在BC边上求作一点P，使得点P到AC的距离等于BP的长．（保留作图痕迹，不写作法）
27. 如图，在矩形 中，请利用尺规作图：分别在边 、 上作点 、 ，使四边形 是菱形.（不写作法保留作图痕迹）
28. 如图，在 中，∠A＝30°，请用尺规作图法，在AC边上求作一点M，使得AM＝2BM.（不写作法，保留作图痕迹）
29. 如图，已知 ，请利用尺规作图法在AB上求作一点P，使得∠PAC＝∠PCA.（不写作法，保留作图痕迹）
30. 如图，在△ABC中，BD是边AC上的高.请用尺规作图法，在BD上求作一点E，使得∠CED+∠ABD＝90°.（保留作图痕迹，不写作法）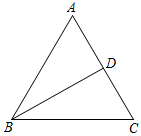
31. 如图，请用尺规作 ，使得 与 BC 相切（不写作法，保留作图痕迹）
32. 如图，在△ABC中，点D为AB中点，请用尺规作图方法，在线段AC上找一点E，使得DE∥BC.（请保留作图痕记，不写作法）
五、综合题
-
33. 如图，已知⊙O的半径为5，PA是⊙O的一条切线，切点为A，连接PO并延长，交⊙O于点B，过点A作AC⊥PB交⊙O于点C、交PB于点D，连接BC，当∠P=30°时，
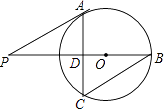(1)、求弦AC的长；(2)、求证：BC∥PA．34. 如图
[问题探究]
(1)、如图1， ABC为等边三角形，边长为6，AD⊥BC，垂足为点D，点E和点F分别是线段和AD和AB上的两个动点，连接CE，EF.则CE+EF的最小值为；(2)、如图2，⊙O为 ABC的外接圆，AB是直径，AC＝BC，点D是直径AB左侧的圆上一点，连接DA，DB，DC.将 ACD绕点C逆时针旋转得到 BCE.若CD＝4，求四边形ADBC的面积；(3)、如图3，⊙O为等边 ABC的外接圆，半径为2，点D在劣弧 上运动（不与点A，B重合），连接DA.DB，DC.设线段DC的长为x.四边形ADBC的面积为S.
①求S与x的函数关系式；
②若点M，N分别在线段CA，CB上运动（不含瑞点），经过探究发现，点D运动到每一个确定的位置. DMN的周长有最小值t，随着点D的运动，t的值会发生变化.求所有t值中的最大值，并求此时四边形ADBC的面积S.
35. 如图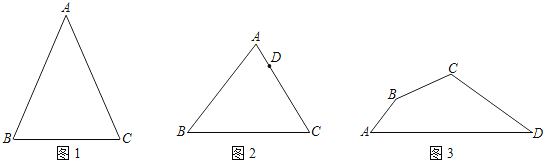
(1)、问题提出：如图1，在△ABC中，已知AB＝AC＝5，BC＝4，在BC上找一点D，使得线段AD将△ABC分成面积相等的两部分，画出线段AD，并写出AD的长为 ▲ .
(2)、问题探究：如图2，点D是△ABC边AC上一定点，在BC上找一点E，使得线段DE将△ABC分成面积相等的两部分，并说明理由.
(3)、问题解决：如图3，四边形ABCD是西安市高新区新近改造过程中的一块不规则空地，为了美化环境，市规划办决定在这块地里种植两种花卉，打算过点C修一条笔直的通道，以便市民出行观赏花卉，要求通道两侧种植花卉的面积相等，经测量AB＝20米，AD＝100米，∠A＝60°，∠ABC＝150°，∠BCD＝120°，若将通道记为CF，请你画出通道CF，并求出通道CF的长.
