山东省聊城临清市2021年中考数学三模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 2sin45°的值等于()A、1 B、 C、 D、22. 如图是由几个相同的小正方体搭成的一个几何体,它的左视图是( )
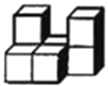 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 不等式组 的最小整数解是( )A、0 B、-1 C、1 D、25. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、6. 如图摆放的一副学生用直角三角板, , 与 相交于点G,当 时, 的度数是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 不等式组 的最小整数解是( )A、0 B、-1 C、1 D、25. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、6. 如图摆放的一副学生用直角三角板, , 与 相交于点G,当 时, 的度数是( )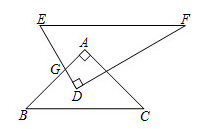 A、135° B、120° C、115° D、105°7. 如图,C , D是⊙O上位于直径AB异侧的两点,若∠ACD=20°,则∠BAD的度数是( )
A、135° B、120° C、115° D、105°7. 如图,C , D是⊙O上位于直径AB异侧的两点,若∠ACD=20°,则∠BAD的度数是( )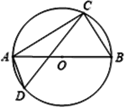 A、70° B、60° C、50° D、40°8. 用加减消元法解二元一次方程组 时,下列方法中无法消元的是( )A、①×2﹣② B、②×(﹣3)﹣① C、①×(﹣2)+② D、①﹣②×39. 如图,在 中, ,高 ,正方形 一边在 上,点 分别在 上, 交 于点 ,则 的长为( )
A、70° B、60° C、50° D、40°8. 用加减消元法解二元一次方程组 时,下列方法中无法消元的是( )A、①×2﹣② B、②×(﹣3)﹣① C、①×(﹣2)+② D、①﹣②×39. 如图,在 中, ,高 ,正方形 一边在 上,点 分别在 上, 交 于点 ,则 的长为( )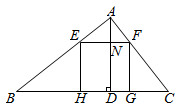 A、 B、 C、 D、10.
A、 B、 C、 D、10.某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
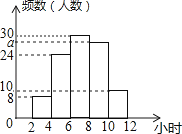 A、4﹣6小时 B、6﹣8小时 C、8﹣10小时 D、不能确定11. 如图,△ABO的顶点A在函数 (x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q . 若四边形MOBP的面积为5,则k的值为( )
A、4﹣6小时 B、6﹣8小时 C、8﹣10小时 D、不能确定11. 如图,△ABO的顶点A在函数 (x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q . 若四边形MOBP的面积为5,则k的值为( )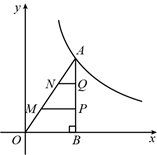 A、9 B、12 C、15 D、1812. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( )
A、9 B、12 C、15 D、1812. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( )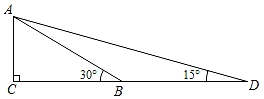 A、 B、 ﹣1 C、 D、
A、 B、 ﹣1 C、 D、二、填空题
-
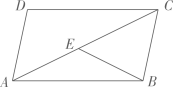
13. 计算: 的结果是 .14. 两个不透明的盒子里各分别装有红色、白色、蓝色三个小球,现从两个盒子中各随机取一个球,则取出的球是同一颜色的概率是 .15. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图, 是平行四边形 的对角线,点 在 上, , ,则 的大小是.
 16. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=60°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE, 点B经过的路径为弧BD,则图中阴影部分的面积为.
16. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=60°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE, 点B经过的路径为弧BD,则图中阴影部分的面积为.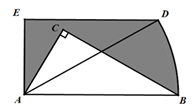 17. 如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……,按这样的方法拼成的第 个正方形比第n个正方形多个小正方形.
17. 如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……,按这样的方法拼成的第 个正方形比第n个正方形多个小正方形.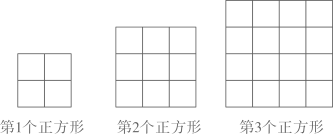
三、解答题
-
18. 先化简,再求值:1+ ÷(2+ ),其中a=2.19. 某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型
频数
频率
跳绳
25
a
实心球
20
50m
b
0.4
拔河
0.15
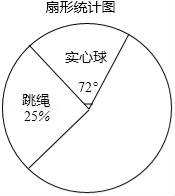 (1)、直接写出a= , b=;(2)、将图中的扇形统计图补充完整(注明项目、百分比);(3)、若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?20. 如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
(1)、直接写出a= , b=;(2)、将图中的扇形统计图补充完整(注明项目、百分比);(3)、若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?20. 如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明. 21. 五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.22. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线.为了测量房屋的高度,在地面上C点测得屋顶 的仰角为 ,此时地面上C点、屋檐上 点、屋顶上A点三点恰好共线,继续向房屋方向走 到达点D时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点G(点C,D, 在同一水平线上).(参考数据: , , , )
21. 五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.22. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线.为了测量房屋的高度,在地面上C点测得屋顶 的仰角为 ,此时地面上C点、屋檐上 点、屋顶上A点三点恰好共线,继续向房屋方向走 到达点D时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点G(点C,D, 在同一水平线上).(参考数据: , , , )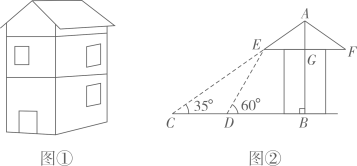 (1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).23. 双曲线 (k为常数,且 )与直线 交于 两点.
(1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).23. 双曲线 (k为常数,且 )与直线 交于 两点.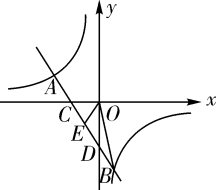 (1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.24. 如图,AB是圆O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB与圆O交于点F,在CD上取一点E,使得EF=EC.
(1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.24. 如图,AB是圆O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB与圆O交于点F,在CD上取一点E,使得EF=EC.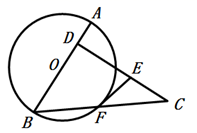 (1)、求证:EF是圆O的切线;(2)、若D是OA的中点,AB=4,求CF的长.25. 如图,在平面直角坐标系中,抛物线 与x轴交于点 ,与y轴交于点C , 且直线 过点B , 与y轴交于点D , 点C与点D关于x轴对称.点P是线段 上一动点,过点P作x轴的垂线交抛物线于点M , 交直线 于点N .
(1)、求证:EF是圆O的切线;(2)、若D是OA的中点,AB=4,求CF的长.25. 如图,在平面直角坐标系中,抛物线 与x轴交于点 ,与y轴交于点C , 且直线 过点B , 与y轴交于点D , 点C与点D关于x轴对称.点P是线段 上一动点,过点P作x轴的垂线交抛物线于点M , 交直线 于点N . (1)、求抛物线的函数解析式;(2)、当 的面积最大时,求点P的坐标;(3)、在(2)的条件下,在y轴上是否存在点Q , 使得以 三点为顶点的三角形是直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的函数解析式;(2)、当 的面积最大时,求点P的坐标;(3)、在(2)的条件下,在y轴上是否存在点Q , 使得以 三点为顶点的三角形是直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.