山东菏泽牡丹区2021年中考数学三模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 下列各数中,无理数是( )A、 B、 C、 D、2. 如果代数式 的值为0,那么实数x满足( )A、 B、 C、 D、3. 如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )
 A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 如图,已知矩形 的三个顶点的坐标分别为 , , ,按以下步骤作图:①以点 为圆心,适当长度为半径作弧,分别交 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径作弧,两弧在 内交于点 ;③作射线 ,交边 于点 ,则点 的坐标为( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 如图,已知矩形 的三个顶点的坐标分别为 , , ,按以下步骤作图:①以点 为圆心,适当长度为半径作弧,分别交 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径作弧,两弧在 内交于点 ;③作射线 ,交边 于点 ,则点 的坐标为( ) A、 B、 C、 D、5. 七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率为( )
A、 B、 C、 D、5. 七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率为( ) A、 B、 C、 D、6. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、 B、 C、 且 D、 且7. 为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了甲、乙两类玩具,其中甲类玩具的进价比乙类玩具的进价每个多5元,经调查:用1000元购进甲类玩具的数量与用750元购进乙类玩具的数量相同.设甲类玩具的进价为x元/个,根据题意可列方程为( )A、 B、 C、 D、8. 如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B , C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK . 设BE的长为x , △DFC的面积为y , 则下列图象中能大致表示y与x的函数关系的是( )
A、 B、 C、 D、6. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、 B、 C、 且 D、 且7. 为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了甲、乙两类玩具,其中甲类玩具的进价比乙类玩具的进价每个多5元,经调查:用1000元购进甲类玩具的数量与用750元购进乙类玩具的数量相同.设甲类玩具的进价为x元/个,根据题意可列方程为( )A、 B、 C、 D、8. 如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B , C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK . 设BE的长为x , △DFC的面积为y , 则下列图象中能大致表示y与x的函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 对于中国而言,2020年是一个新的时间坐标,过去40年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将数字820000000科学记数法表示为 .10. 关于x的不等式组 的解集如图所示,则m的值为.
 11. 如果一组数据-1、0、3、5、x的极差为7,那么x的值可以是 .12. 如图,在半径为1的扇形 中, ,点 是弧 上任意一点(不与点 , 重合), , ,垂足分别为 , ,则 的长为 .
11. 如果一组数据-1、0、3、5、x的极差为7,那么x的值可以是 .12. 如图,在半径为1的扇形 中, ,点 是弧 上任意一点(不与点 , 重合), , ,垂足分别为 , ,则 的长为 .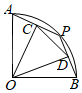 13. 如图,以点 为位似中心,把 放大2倍得到 ',① ;② ;③ ;④点 、 、 三点在同一直线上.则以上四种说法正确的是 .
13. 如图,以点 为位似中心,把 放大2倍得到 ',① ;② ;③ ;④点 、 、 三点在同一直线上.则以上四种说法正确的是 .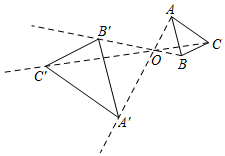 14. 如图,在平面直角坐标系 中,直线 : 交y轴于点 ,点 , ,…, 在直线 上,点 , , ,…, 在 轴的正半轴上,若 , , ,…, ,依次均为等腰直角三角形,点 的坐标是 .
14. 如图,在平面直角坐标系 中,直线 : 交y轴于点 ,点 , ,…, 在直线 上,点 , , ,…, 在 轴的正半轴上,若 , , ,…, ,依次均为等腰直角三角形,点 的坐标是 .
三、解答题
-
15. 计算: .16. 先化简再求值: ,其中 , .17. 如图,在 中, , 是 的中点, 是 上的点,过点 作 交 的延长线于点 ,若四边形 是菱形,求证: .
 18. 如图,一扇窗户打开后可以用窗钩 将其固定,窗钩的一个端点 固定在窗户底边 上,且与转轴底端 之间的距离为20cm,窗钩的另一个端点 在窗框边上的滑槽 上移动,滑槽 的长度为17cm, 、 、 构成一个三角形.当窗钩端点 与点 之间的距离是7cm的位置时(如图2),窗户打开的角 的度数为 .求窗钩 的长度(精确到1cm).(参考数据: , , )
18. 如图,一扇窗户打开后可以用窗钩 将其固定,窗钩的一个端点 固定在窗户底边 上,且与转轴底端 之间的距离为20cm,窗钩的另一个端点 在窗框边上的滑槽 上移动,滑槽 的长度为17cm, 、 、 构成一个三角形.当窗钩端点 与点 之间的距离是7cm的位置时(如图2),窗户打开的角 的度数为 .求窗钩 的长度(精确到1cm).(参考数据: , , ) 19. 每年的4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社甲乙两名同学为了更好的了解全校学生课外阅读情况,分别随机调查了20名学生每周用于课外阅读的时间,将收集到的数据进行了整理,部分信息如下:
19. 每年的4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社甲乙两名同学为了更好的了解全校学生课外阅读情况,分别随机调查了20名学生每周用于课外阅读的时间,将收集到的数据进行了整理,部分信息如下:数据收集:甲同学从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:分钟:40;15;20;85;71;90;43;60;120;70;71;80;10;42;65;107;85;71;125;130
乙同学从八年级随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:分钟)10;42;86;25;70;55;76;30;18;120;102;82;60;140;82;40;114;100;90;98
数据描述:
将阅读时间分为四个等级:
甲同学按下表整理样本数据:
等级
A
B
C
D
人数
a
9
b
3
乙同学绘制扇形统计图如图:

分析数据:样本数据的平均数、中位数、众数如下表所示:
平均数
中位数
众数
甲
70
c
71
乙
72
79
d
根据以上信息,回答下列问题:
(1)、 , , , ; 度;(2)、甲乙两名同学中,哪名同学随机调查的数据能较好地反映岀该校学生每周用于课外阅读时间情况,并简要说明另一名同学调查的不足之处;(3)、根据符合题意统计的这组每周课外阅读时间的样本数据,若该校学生有1500人,请估计每周课外阅读时间在80分钟(含80分钟)以上的学生有多少人?20. 已知直线 经过点 ,且与 轴交于点 ,(1)、求点 的坐标:(2)、如果一个反比例函数的图象与线段 的延长线交于点 ,且 ,求这个反比例函数的解析式. 21. 为配合崇明“花博会”,花农黄老伯培育了甲、乙两种花木各若干株.如果培育甲、乙两种花木各一株,那么共需成本500元;如果培育甲种花木3株和乙种花木2株,那么共需成本1200元.(1)、求甲、乙两种花木每株的培育成本分别为多少元?(2)、市场调查显示,甲种花木的市场售价为每株300元,乙种花木的市场售价为每株500元.黄老伯决定在将成本控制在不超过30000元的前提下培育两种花木,并使总利润不少于18000元.若黄老伯培育的乙种花木的数量比甲种花木的数量的3倍少10株,请问黄老伯应该培育甲、乙两种花木各多少株?22. 图,在 中, ,以 为直径的 交 于点D , E是 中点,连接 .
21. 为配合崇明“花博会”,花农黄老伯培育了甲、乙两种花木各若干株.如果培育甲、乙两种花木各一株,那么共需成本500元;如果培育甲种花木3株和乙种花木2株,那么共需成本1200元.(1)、求甲、乙两种花木每株的培育成本分别为多少元?(2)、市场调查显示,甲种花木的市场售价为每株300元,乙种花木的市场售价为每株500元.黄老伯决定在将成本控制在不超过30000元的前提下培育两种花木,并使总利润不少于18000元.若黄老伯培育的乙种花木的数量比甲种花木的数量的3倍少10株,请问黄老伯应该培育甲、乙两种花木各多少株?22. 图,在 中, ,以 为直径的 交 于点D , E是 中点,连接 .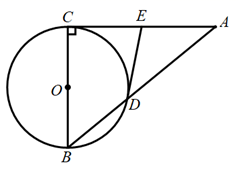 (1)、判断 与 的位置关系并说明理由;(2)、设 与 的交点为F , 若 ,求 的长.23. 如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)、判断 与 的位置关系并说明理由;(2)、设 与 的交点为F , 若 ,求 的长.23. 如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F. (1)、当PE⊥AB,PF⊥BC时,如图1,则 的值为;(2)、现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;(3)、在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.24. 如图,已知抛物线 图象经过 , 两点.
(1)、当PE⊥AB,PF⊥BC时,如图1,则 的值为;(2)、现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;(3)、在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.24. 如图,已知抛物线 图象经过 , 两点. (1)、求抛物线的解析式;(2)、若 是抛物线上位于第一象限内的点, 是线段 上的一个动点(不与 、 重合),过点 分别作 交 于 , 交 于 .
(1)、求抛物线的解析式;(2)、若 是抛物线上位于第一象限内的点, 是线段 上的一个动点(不与 、 重合),过点 分别作 交 于 , 交 于 .①求证:四边形 是矩形;
②连接 ,线段 的长是否存在最小值,若存在,求出 的最小值:若不存在,请说明理由.