江西省赣州市章贡区2021年中考数学5月模拟试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 分式 的值是零,则 的值为( )A、5 B、-5 C、-2 D、22. 下面几种中式窗户图形既是轴对称又是中心对称的是( )A、
 B、
B、 C、
C、 D、
D、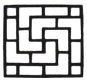 3. 下列运算中,正确的是( )A、(a2)3=a5 B、 C、 D、a3•a3=2a64. 如图的两个几何体各由5个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
3. 下列运算中,正确的是( )A、(a2)3=a5 B、 C、 D、a3•a3=2a64. 如图的两个几何体各由5个相同的小正方体搭成,比较两个几何体的三视图,正确的是( ) A、仅俯视图不同 B、仅主视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都不相同5. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
A、仅俯视图不同 B、仅主视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都不相同5. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( ) A、 B、 C、 D、6. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,CD⊥AB于点D . 点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E , 作PF⊥BC于点F . 设点P运动的路程为x , 四边形CEPF的面积为y , 则能反映y与x之间函数关系的图象( )
A、 B、 C、 D、6. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,CD⊥AB于点D . 点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E , 作PF⊥BC于点F . 设点P运动的路程为x , 四边形CEPF的面积为y , 则能反映y与x之间函数关系的图象( ) A、
A、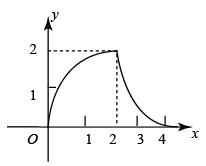 B、
B、 C、
C、 D、
D、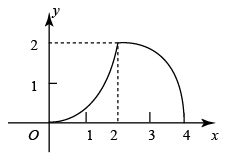
二、填空题
-
7. 今年6月13日是我国第四个文化和自然遗产日.目前,我国世界遗产总数据居世界首位.其中自然遗产总面积约68000 km2 , 将数68000用科学记数法表示应为 .8. 已知4个数据:x , 5,5,8. 如果这组数据的众数与平均数相等,那么这组数据的中位数是 .9. 关于x的方程x2﹣kx+2=0有一个根是1,则方程的另一个解为 .10. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托:折回索子却量竿,却比竿子短一托,”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺.则正确的方程是 .11. 如图, 是正方形ABCD的内切圆,切点分别为E、F,G,H,ED与 相交于点M,则sin∠MFG的值为 .
 12. 已知△ABC是边长为2的等边三角形,△ACD 是一个含30°角的直角三角形,△ABC和△ACD组成一个凸四边形ABCD , 则线段BD的长为 .
12. 已知△ABC是边长为2的等边三角形,△ACD 是一个含30°角的直角三角形,△ABC和△ACD组成一个凸四边形ABCD , 则线段BD的长为 .三、解答题
-
13.(1)、解不等式: (x﹣1)﹣1>2x;(2)、如图AB∥CD . EF交AB于G , 交CD于F , FH平分∠EFD , 交AB于H , ∠AGE=50°,求∠BHF的度数.
 14. 先化简,再求值:a2﹣b(a﹣b)﹣(a﹣b)2 , 其中a=﹣2﹣ ,b= ﹣2.15. 如图,点A、B、C是4× 4网格上的格点,连接点A、B、C得△ABC , 请分别在下列图中使用无刻度的直尺按要求画图.
14. 先化简,再求值:a2﹣b(a﹣b)﹣(a﹣b)2 , 其中a=﹣2﹣ ,b= ﹣2.15. 如图,点A、B、C是4× 4网格上的格点,连接点A、B、C得△ABC , 请分别在下列图中使用无刻度的直尺按要求画图. (1)、在图1中,在AC上找一点M , 使 ;(2)、在图2中,在△ABC 内部(不含边界)找一点N , 使 .16. 某地为抗击新冠肺炎要在某校选拔一名志愿者.经过面试和健康检查,结果优秀青年教师小新和小纯入选.接着通过抓球来确定人选.
(1)、在图1中,在AC上找一点M , 使 ;(2)、在图2中,在△ABC 内部(不含边界)找一点N , 使 .16. 某地为抗击新冠肺炎要在某校选拔一名志愿者.经过面试和健康检查,结果优秀青年教师小新和小纯入选.接着通过抓球来确定人选.抓球规则:在不透明的布袋里装有除颜色之外均相同的2个红球和1个白球,小新先取出一个球,记住颜色后放回,然后小纯再取出一个球,若两人取出的球都是红球,则小新胜出;若取出的球是一红一白,则小纯胜出.
(1)、小新先取出一个黑球是事件,取出一个球的可能性更大;(2)、你认为这个规则对双方公平吗?请用列表法或画树状图的方法说明.17. 如图所示,在平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A2B3与△B2A2B1关于点B2成中心对称. (1)、直接写出B1 , B2 , B3 , 的坐标分别为 , , ;(2)、连接A1B2 , 求A1B2的长.18. 如图,在平面直角坐标系中,点B坐标是(3,4),BA⊥x轴于点A , 点B在反比例函数y= (k>0,x>0)的图象上,将△OAB向右平移,得到△O'A'B',O'B'交双曲线于点C (3a , a).
(1)、直接写出B1 , B2 , B3 , 的坐标分别为 , , ;(2)、连接A1B2 , 求A1B2的长.18. 如图,在平面直角坐标系中,点B坐标是(3,4),BA⊥x轴于点A , 点B在反比例函数y= (k>0,x>0)的图象上,将△OAB向右平移,得到△O'A'B',O'B'交双曲线于点C (3a , a).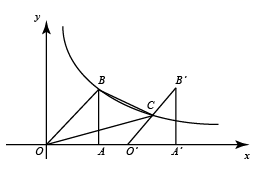 (1)、求k , a的值;(2)、求出△OAB向右平移到 的距离;(3)、连接OB , BC , OC , 求△OBC的面积.19. 果农老王今年种植了甲、乙两个大棚的葡萄.为了了解大棚里所种植的“夏黑“葡萄的产量情况,现从两个大棚里分别随机抽取了20串葡萄,对它们的质量(单位:g)进行整理、描述和分析,下面给出了部分信息:
(1)、求k , a的值;(2)、求出△OAB向右平移到 的距离;(3)、连接OB , BC , OC , 求△OBC的面积.19. 果农老王今年种植了甲、乙两个大棚的葡萄.为了了解大棚里所种植的“夏黑“葡萄的产量情况,现从两个大棚里分别随机抽取了20串葡萄,对它们的质量(单位:g)进行整理、描述和分析,下面给出了部分信息:(葡萄的质量用x表示,共分为五组,A组:400≤x<450,B组:450≤x<500,C组:500≤x<550,D组:550≤x<600,E组:600≤x<650).
甲大棚20串葡萄的重量分别为:
545,560,414,565,640,560,590,542,425,560,
630,580,466,530,487,625,490,513,508,540,
乙大棚20串葡萄的重量在C组中的数据是:520,545,530,520,533,522
甲、乙两大棚随机抽取的葡萄的质量数据统计表如图表所示:
甲大棚
乙大棚
平均质量
538.5
536.6
中位数
543.5
b
众数
a
562
方差
3840.7
3032.5

根据以上信息解答下列问题:
(1)、请直接写出上述统计表中a , b的值:a= , b=;(2)、重量在600 g/串及以上的视为“佳品葡萄”,求出本次乙大棚中抽取的20串葡萄中“佳品葡萄”有多少串?(3)、若老王甲、乙两大棚的葡萄总共有3600串.请估计甲、乙两大棚中质量在600g及以上的葡萄共有多少串?20. 图1是一个闭合时的夹子,图2是该夹子的侧面简化示意图,夹子两边为AC , BD (闭合时点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E , OF⊥BD于点F , OE=OF=1cm,AC=BD=6cm,CE=DF , CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动. (1)、当E , F两点的距离最大时,求∠EOF增加了多少度(结果精确到1°,参考数据:
(1)、当E , F两点的距离最大时,求∠EOF增加了多少度(结果精确到1°,参考数据:tan67.4°≈2.40,tan15.5°=0.278,tan74.5°≈3.60):
(2)、当夹子的开口最大(即点C与点D重合)时,求A , B两点间的距离.21. 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. (1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.22. 如图1,菱形ABCD中,AB=6.∠B=60°,四边形EFGB的顶点E , G分别在边BC和AB上,EF∥CD , FG∥AD , 连接FD .
(1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.22. 如图1,菱形ABCD中,AB=6.∠B=60°,四边形EFGB的顶点E , G分别在边BC和AB上,EF∥CD , FG∥AD , 连接FD .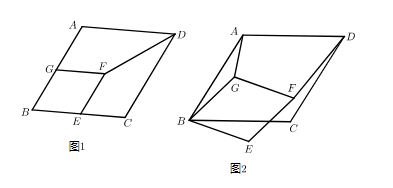 (1)、若DF平分∠ADC , 求证:四边形EFGB为菱形;(2)、在(1)中的条件下,当EC=2时,将四边形EFGB绕点B顺时针旋转至图2所示的位置,连接AG .
(1)、若DF平分∠ADC , 求证:四边形EFGB为菱形;(2)、在(1)中的条件下,当EC=2时,将四边形EFGB绕点B顺时针旋转至图2所示的位置,连接AG .①猜想AG与DF的数量关系,并加以证明;
②当GF过点C时,求sin∠GBC的值.
23. 已知抛物线y1:y1=a (x﹣h1)2+k1与x轴交于点O(0,0),A1(2,0),且抛物线y1的顶点M1在直线y=﹣x上.
 (1)、直接写出抛物线y1的表达式y1= , 顶点M1的坐标为;(2)、如图1,将抛物线y1沿直线y=﹣x向右下方平移,与x轴交于点A1 , A2 . 得到抛物线y2:y2=a(x﹣h2)2+k2 , 顶点为M2;将抛物线y2沿直线y=﹣x向右下方平移,与x轴交于点A2 , A3 , 得到抛物线y3:y3=a (x﹣h3)2+k3 , 顶点为M3;依此类推…
(1)、直接写出抛物线y1的表达式y1= , 顶点M1的坐标为;(2)、如图1,将抛物线y1沿直线y=﹣x向右下方平移,与x轴交于点A1 , A2 . 得到抛物线y2:y2=a(x﹣h2)2+k2 , 顶点为M2;将抛物线y2沿直线y=﹣x向右下方平移,与x轴交于点A2 , A3 , 得到抛物线y3:y3=a (x﹣h3)2+k3 , 顶点为M3;依此类推…①求A2和M2的坐标,并直接写出A3和M3的坐标;
②求MnMn﹣1的长.
(3)、如图2,若Q是抛物线y1上的一个动点,过点P(﹣2,0)引射线PQ , 在射线上取点N , 使QN=QP .①当点Q与M1重合时,则对应的点N坐标为 ▲ ;
②请在图中描出随着点Q运动中对应的点N , 再用平滑的曲线连接起来,猜想曲线是什么函数的图象,并求点N所在曲线的函数的解析式.