黑龙江省齐齐哈尔市铁峰区2021年中考数学二模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 -2021 B、2021 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、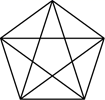 4. 冉冉的妈妈在网上销售装饰品.最近一周, 每天销售某种装饰品的个数为:.11,10,11,13,11,13,15关于这组数据,冉冉得出如下结果,其中错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是135. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、
4. 冉冉的妈妈在网上销售装饰品.最近一周, 每天销售某种装饰品的个数为:.11,10,11,13,11,13,15关于这组数据,冉冉得出如下结果,其中错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是135. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、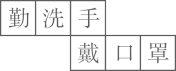 B、
B、 C、
C、 D、
D、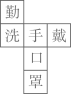 6. 和平中学为了排污,需铺设一段全长为7200米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前4天完成任务,设原计划每天铺设 米,下面所列方程正确的是( )A、 B、 C、 D、7. 若关于x的不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、8. 已知关于 的分式方程 的解是非负数,则 的取值范围是( )A、 B、 C、 且 D、 且9. 今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )A、2种 B、3种 C、4种 D、5种10. 如图,二次函数 的图象与 轴交于 , 两点,与 轴正半轴交于点 ,它的对称轴为直线 .则下列选项中① ;② ;③ ;④ :⑤当 ( 为实数)时, ,其中正确的有( )
6. 和平中学为了排污,需铺设一段全长为7200米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前4天完成任务,设原计划每天铺设 米,下面所列方程正确的是( )A、 B、 C、 D、7. 若关于x的不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、8. 已知关于 的分式方程 的解是非负数,则 的取值范围是( )A、 B、 C、 且 D、 且9. 今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )A、2种 B、3种 C、4种 D、5种10. 如图,二次函数 的图象与 轴交于 , 两点,与 轴正半轴交于点 ,它的对称轴为直线 .则下列选项中① ;② ;③ ;④ :⑤当 ( 为实数)时, ,其中正确的有( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. “我的连云港” 是全市统一的城市综合移动应用服务端.一年来,实名注册用户超过1600000人.数据“1600000”用科学记数法表示为.12. 如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: , 使得平行四边形ABCD为菱形.
 13. 已知圆锥的侧面积展开图面积是 ,母线长为10,则圆锥的底面圆半径等于.14. 如图,函数 的图象上有一点 ,过 点做 垂直 轴, 为垂足,连接 ,过 边的三等分点 、 分别作 轴的平行线交 于点 、 .若四边形 的面积为1,则k的值为 .
13. 已知圆锥的侧面积展开图面积是 ,母线长为10,则圆锥的底面圆半径等于.14. 如图,函数 的图象上有一点 ,过 点做 垂直 轴, 为垂足,连接 ,过 边的三等分点 、 分别作 轴的平行线交 于点 、 .若四边形 的面积为1,则k的值为 . 15. 在 中, , ,直线 垂直平分 (垂足为 ,直线 与 的另一边相交于点 ,且 时,则 .16. 在 中, ,两锐角的度数之比为1:2,最短边 长为2,且 , 交边 所在直线于点 ,则 的长为 .17. 如图,直线 的解析式为 与 轴交于点 ,与 轴交于点 ,以 为边作正方形 ,点 坐标为 ,过点 作 交 于点 ,交 轴于点 ,过点 作 轴的垂线交 于点 ,连接 ;以 为边作正方形 ,点 的坐标为 .过点 作 交 于 ,交 轴于点 ,过点 作 轴的垂线交 于点 ,连接 ;以 为边作正方形 ,……,则 的长为 .
15. 在 中, , ,直线 垂直平分 (垂足为 ,直线 与 的另一边相交于点 ,且 时,则 .16. 在 中, ,两锐角的度数之比为1:2,最短边 长为2,且 , 交边 所在直线于点 ,则 的长为 .17. 如图,直线 的解析式为 与 轴交于点 ,与 轴交于点 ,以 为边作正方形 ,点 坐标为 ,过点 作 交 于点 ,交 轴于点 ,过点 作 轴的垂线交 于点 ,连接 ;以 为边作正方形 ,点 的坐标为 .过点 作 交 于 ,交 轴于点 ,过点 作 轴的垂线交 于点 ,连接 ;以 为边作正方形 ,……,则 的长为 .
三、解答题
-
18.(1)、计算: ;(2)、分解因式: .19. 解方程: .20. 随着疫情的发展,“勤洗手,戴口罩”六字已深入人心,小华就某城区公众对在公共场合制止不戴口罩的态度进行了随机抽样调查,主要有四种态度:A . 赞成保安对不戴口罩的出面制止:B . 赞成群众对不戴口罩的出面制止:C . 赞成防疫人员对不戴口罩的出面制止;D . 无所谓,他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
 (1)、求这次抽样的公众有多少人?(2)、请将统计图①补充完整;(3)、在统计图②中,求“无所谓”部分所对应的圆心角是多少度?(4)、若该城区人口有20万人,估计赞成“防疫人员对不戴口罩的出面制止”的有多少万人?(5)、小华在该城区随机对路人进行调查,请你根据以上信息,直接写出赞成“防疫人员对不戴口罩的出面制止”的概率是 .21. 如图,在以 为直径的 中, ,弦 与 交于点 ,过点 、 分别作 的切线交于点 ,并与 延长线交于点 .
(1)、求这次抽样的公众有多少人?(2)、请将统计图①补充完整;(3)、在统计图②中,求“无所谓”部分所对应的圆心角是多少度?(4)、若该城区人口有20万人,估计赞成“防疫人员对不戴口罩的出面制止”的有多少万人?(5)、小华在该城区随机对路人进行调查,请你根据以上信息,直接写出赞成“防疫人员对不戴口罩的出面制止”的概率是 .21. 如图,在以 为直径的 中, ,弦 与 交于点 ,过点 、 分别作 的切线交于点 ,并与 延长线交于点 . (1)、求证: .(2)、已知: , 的半径为3,求 的长.22. 、 两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从 地驶向甲地,中途因故停车1小时后,继续按原路原速驶向 地;快车从 地驶向 地,在到达 地后,立即按原路原速返回到 地,在两车行驶的过程中,两车距 地的路程 (千米)与两车行驶时间 (小时)之间的函数图象如图所示.请结合图象解答下列问题:
(1)、求证: .(2)、已知: , 的半径为3,求 的长.22. 、 两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从 地驶向甲地,中途因故停车1小时后,继续按原路原速驶向 地;快车从 地驶向 地,在到达 地后,立即按原路原速返回到 地,在两车行驶的过程中,两车距 地的路程 (千米)与两车行驶时间 (小时)之间的函数图象如图所示.请结合图象解答下列问题: (1)、求快、慢两车在行驶过程中的速度;(2)、求快车从 地返回 地的过程中, 与 的函数解析式;(3)、出发多长时间,两车相距的路程是75千米?(直接写出答案).23. 综合与实践(1)、数学问题:
(1)、求快、慢两车在行驶过程中的速度;(2)、求快车从 地返回 地的过程中, 与 的函数解析式;(3)、出发多长时间,两车相距的路程是75千米?(直接写出答案).23. 综合与实践(1)、数学问题:如图1, 是等腰直角三角形,过斜边的中点 作正方形 ,分别交 , 于点 , ,则 , , 之间的数量关系为 .
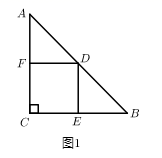 (2)、问题解决:
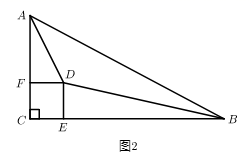
(2)、问题解决:如图2,在任意 内,找一点 ,过点 作正方形 ,分别交 , 于点 , ,若 ,求 的度数;
 (3)、拓展提升:
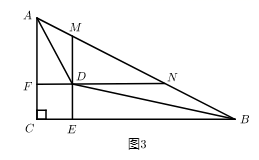
(3)、拓展提升:如图3,在(2)的条件下,分别延长 , ,交 于点 , ,则 , , 的数量关系为 .
 (4)、在(3)的条件下,若 , ,则 .24. 综合与探究
(4)、在(3)的条件下,若 , ,则 .24. 综合与探究如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .
 (1)、求抛物线的函数表达式:(2)、若点 在 轴的下方,当 的面积是 时,求 的面积;(3)、在直线 上有一点 ,连接 , ,则 的最小值为;(4)、在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点的四边形是平行四边形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式:(2)、若点 在 轴的下方,当 的面积是 时,求 的面积;(3)、在直线 上有一点 ,连接 , ,则 的最小值为;(4)、在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点的四边形是平行四边形,若存在,请直接写出点 的坐标;若不存在,请说明理由.