黑龙江省齐齐哈尔市龙沙区2021年中考数学三模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 下列各数中,化简结果为-2021的是( )A、 B、 C、 D、2. 如图,两个全等的正方形的四种不同摆放中,中心对称图形有( )
 A、1个 B、2个 C、3个 D、4个3. 下列计算正确的是( )A、 B、 C、 D、4. 四个相同的不透明的袋子都装有除颜色外无其它差别的小球.从这四个袋子中分别随机摸出一个球,摸到红球可能性最大的是( )A、有1个红球和2个白球的袋子 B、有2个红球和3个白球的袋子 C、有3个红球和4个白球的袋子 D、有4个红球和5个白球的袋子5. 在同一平面直角坐标系中,函数 与 的图象不可能是( )A、
A、1个 B、2个 C、3个 D、4个3. 下列计算正确的是( )A、 B、 C、 D、4. 四个相同的不透明的袋子都装有除颜色外无其它差别的小球.从这四个袋子中分别随机摸出一个球,摸到红球可能性最大的是( )A、有1个红球和2个白球的袋子 B、有2个红球和3个白球的袋子 C、有3个红球和4个白球的袋子 D、有4个红球和5个白球的袋子5. 在同一平面直角坐标系中,函数 与 的图象不可能是( )A、 B、
B、 C、
C、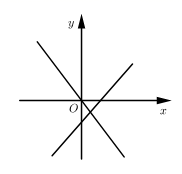 D、
D、 6. 已知一组正整数1、2、3、 、 的平均数为2,且众数是唯一的,则 的值为( )A、1 B、3 C、4 D、97. 若关于 的分式方程 有一个正整数解,则整数a的值为( )A、-1 B、0 C、1 D、1或-18. 若一次购买单价分别为7元、5元的两款笔记本共用了54元,则7元笔记本最少买( )A、2本 B、3本 C、4本 D、7本9. 如图,点 是等边 内一点, , , ,若将 绕着点 逆时针旋转 后得到 .则 的值为( )
6. 已知一组正整数1、2、3、 、 的平均数为2,且众数是唯一的,则 的值为( )A、1 B、3 C、4 D、97. 若关于 的分式方程 有一个正整数解,则整数a的值为( )A、-1 B、0 C、1 D、1或-18. 若一次购买单价分别为7元、5元的两款笔记本共用了54元,则7元笔记本最少买( )A、2本 B、3本 C、4本 D、7本9. 如图,点 是等边 内一点, , , ,若将 绕着点 逆时针旋转 后得到 .则 的值为( ) A、 B、 C、 D、10. 如图,抛物线 顶点坐标为 ,对于下列结论:① ;② ;③ ;④若方程 没有实数根,则 .其中正确的结论有( )
A、 B、 C、 D、10. 如图,抛物线 顶点坐标为 ,对于下列结论:① ;② ;③ ;④若方程 没有实数根,则 .其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 截止2021年5月26日全球新冠肺炎病例累计确诊逾16842万例,16842万用科学记数法表示为 .12. 在函数 中,自变量 的取值范围是 .13. 如图,点 在 内部, ,若添加一个条件: . 则 是等边三角形.
 14. 若干个相同的小正方体组成的几何体的主视图和左视图如图所示则组成这个几何体的小正方体最多为个.
14. 若干个相同的小正方体组成的几何体的主视图和左视图如图所示则组成这个几何体的小正方体最多为个. 15. 已知等边三角形 的边长为4,线段 ,且 ,直线 与直线 交于点 ,则 的面积为 .16. 如图,双曲线 与线段 交于点 、 两点,点 坐标为 ,连接 , 的面积为6,则 .
15. 已知等边三角形 的边长为4,线段 ,且 ,直线 与直线 交于点 ,则 的面积为 .16. 如图,双曲线 与线段 交于点 、 两点,点 坐标为 ,连接 , 的面积为6,则 . 17. 在平面直角坐标系中,点 在 轴的正半轴上, , , , , , .按此规律,则 的长为 .
17. 在平面直角坐标系中,点 在 轴的正半轴上, , , , , , .按此规律,则 的长为 .
三、解答题
-
18.(1)、计算:(2)、因式分解:19. 解方程:20. 某校为了了解八年级学生线上课堂发言情况,将随机抽取的该年级部分学生某一天在线上课堂上发言次数统计如下表,并绘制了如图所示的两幅不完整的统计图.请给合图中相关数据回答下列问题:
组别
发言次数
A
B
C
D
E

 (1)、此次调查的样本容量为 , , ;(2)、请补全直方图;(3)、在扇形统计图中, 组所对应的圆心角的度数为°, 组所占的百分比为%;(4)、该年级共有学生1500人,估计全年级这天发言次数不少于6次的有人.21. 如图,在 中, ,点 在 边上, 为 的半径, 是 的切线,切点为点 , , .
(1)、此次调查的样本容量为 , , ;(2)、请补全直方图;(3)、在扇形统计图中, 组所对应的圆心角的度数为°, 组所占的百分比为%;(4)、该年级共有学生1500人,估计全年级这天发言次数不少于6次的有人.21. 如图,在 中, ,点 在 边上, 为 的半径, 是 的切线,切点为点 , , . (1)、求证: 是 的切线;(2)、求阴影部分的面积.22. 甲、乙两地相距200千米,货车从甲地出发,行驶1小时后在途中的丙地出现故障,技术人员乘轿车以100千米/小时的速度从甲地赶来维修(沟通时间忽略不计).到达丙地修好车后以原速原路返回,同时货车改变速度前往乙地.两车距乙地的路程 (千米)与货车驶时间 (小时)之间的函数关系如图所示,请结合图象回答下列问题.
(1)、求证: 是 的切线;(2)、求阴影部分的面积.22. 甲、乙两地相距200千米,货车从甲地出发,行驶1小时后在途中的丙地出现故障,技术人员乘轿车以100千米/小时的速度从甲地赶来维修(沟通时间忽略不计).到达丙地修好车后以原速原路返回,同时货车改变速度前往乙地.两车距乙地的路程 (千米)与货车驶时间 (小时)之间的函数关系如图所示,请结合图象回答下列问题. (1)、货车出现故障前后的速度分别为、千米/小时;(2)、货车在丙地停留了小时;(3)、求图中线段 的函数关系式:(4)、轿车出发后,又过了小时,两车相距路程为40千米.23. 综合与实践
(1)、货车出现故障前后的速度分别为、千米/小时;(2)、货车在丙地停留了小时;(3)、求图中线段 的函数关系式:(4)、轿车出发后,又过了小时,两车相距路程为40千米.23. 综合与实践 (1)、操作探究
(1)、操作探究如图1,将矩形 折叠,使点 与点 重合,折痕为 , 与 交于点 .请回答下列问题:
①与 全等的三角形为 ▲ , 与 相似的三角形为 ▲ . 并证明你的结论:(相似比不为1,只填一个即可):
②若连接 、 ,请判断四边形 的形状: ▲ . 并证明你的结论;
(2)、拓展延伸如图2,矩形 中, , ,点 、 分別在 、 边上,且 ,将矩形折叠,使点 与点 重合,折痕为 , 与 交于点 ,连接 .
①设 , ,则 与 的数量关系为;
②设 , ,请用含 的式子表示 :;
③ 的最小值为 .
24. 综合与探究如图,在平面直角坐标系中,抛物线 与 轴交于点 、 两点(点 在点 左侧),与 轴交于点 . 、 的长是不等式组 的整数解 ,点 在抛物线上.
 (1)、求抛物线的解析式及 的值;(2)、 轴上的点 使 + 的值最小,则 ;(3)、将抛物线向上平移,使点 落在点 处.当 时,抛物线向上平移了个单位;(4)、点 在 轴上,平面直角坐标系内存在点 使以点 、 、 、 为顶点的四边形为菱形,请直接写出点 的坐标.
(1)、求抛物线的解析式及 的值;(2)、 轴上的点 使 + 的值最小,则 ;(3)、将抛物线向上平移,使点 落在点 处.当 时,抛物线向上平移了个单位;(4)、点 在 轴上,平面直角坐标系内存在点 使以点 、 、 、 为顶点的四边形为菱形,请直接写出点 的坐标.