陕西省初中数学历年真题与模拟汇编:函数
试卷更新日期:2021-07-07 类型:二轮复习
一、单选题
-
1. 若正比例函数 的图象经过点O(a-1,4),则a的值为( )A、-1 B、0 C、1 D、22. 若一个正比例函数的图象经过A(3,﹣6),B(m,﹣4)两点,则m的值为( )A、2 B、8 C、﹣2 D、﹣83. 已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 设点A(a,b)是正比例函数y=﹣ x图象上的任意一点,则下列等式一定成立的是( )A、2a+3b=0 B、2a﹣3b=0 C、3a﹣2b=0 D、3a+2b=05. 在平面直角坐标系中,若将一次函数 的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、66. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
…
-2
0
1
3
…
…
6
-4
-6
-4
…
下列各选项中,正确的是
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 时,y的值随x值的增大而增大7. 在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A、2 B、3 C、4 D、69. 在同一平面直角坐标系中,若抛物线 与 关于y轴对称,则符合条件的m,n的值为( )A、m= ,n= B、m=5,n= -6 C、m= -1,n=6 D、m=1,n= -210. 在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )A、(2,0) B、(-2,0) C、(6,0) D、(-6,0)11. 若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为( )
A、(-2,0) B、(2,0) C、(-6,0) D、(6,0)12. 对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
13. 已知一次函数y=2x+4的图象分别交x轴、y轴于A、B两点,若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C,且AB=2BC,则这个反比例函数的表达式为 .14. 若 , 是反比例函数 图象上的两点,则 、 的大小关系是 (填“>”、“=”或“<”)15. 在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y= (k≠0)的图象经过其中两点,则m的值为.16. 若一个反比例函数的图象经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为17. 如图,在平面直角坐标系中,正比例函数y=kx与反比例函数 的图象交于A,B两点,过A作y轴的垂线,交反比例函数 (x>0)的图象于点C,连接BC,若S△ABC=8,则k的值为.
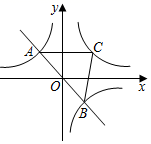 18. 如图,在平面直角坐标系中,一条过原点的直线与反比例函数 的图象相交于 两点,若 , ,则该反比例函数的表达式为.
18. 如图,在平面直角坐标系中,一条过原点的直线与反比例函数 的图象相交于 两点,若 , ,则该反比例函数的表达式为.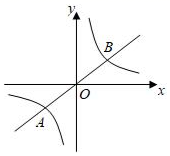
三、解答题
-
19. 已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
四、综合题
-
20. 昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
 (1)、求线段AB所表示的函数关系式;(2)、已知昨天下午3点时,小明距西安112千米,求他何时到家?21. 在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离 与时间 之间的关系如图所示.
(1)、求线段AB所表示的函数关系式;(2)、已知昨天下午3点时,小明距西安112千米,求他何时到家?21. 在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离 与时间 之间的关系如图所示.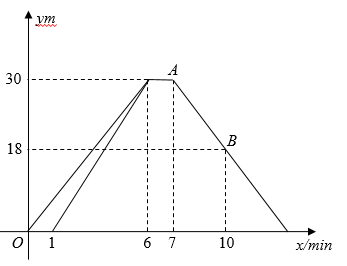 (1)、在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是 ;(2)、求 的函数表达式;(3)、求“猫”从起点出发到返回至起点所用的时间.22. 如图
(1)、在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是 ;(2)、求 的函数表达式;(3)、求“猫”从起点出发到返回至起点所用的时间.22. 如图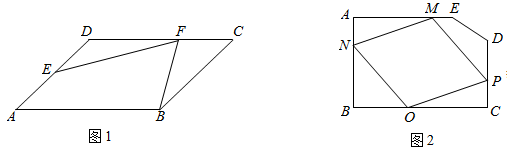 (1)、问题提出
(1)、问题提出如图1,在 中, , , ,E是 的中点,点F在 上且 求四边形 的面积.(结果保留根号)
(2)、问题解决某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上建一个五边形河畔公园 按设计要求,要在五边形河畔公园 内挖一个四边形人工湖 ,使点O、P、M、N分别在边 、 、 、 上,且满足 , .已知五边形 中, , , , , .满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形 面积的最小值及这时点 到点 的距离;若不存在,请说明理由.
23. 已知抛物线 与x轴交于点A、B(其中A在点B的左侧),与y轴交于点C.(1)、求点B、C的坐标;(2)、设点 与点C关于该抛物线的对称轴对称在y轴上是否存在点P,使 与 相似且 与 是对应边?若存在,求点P的坐标;若不存在,请说明理由.24. 某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示. (1)、求y与x之间的函数关系式;(2)、当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?25. 根据记录,从地面向上11km以内,每升高1km,气温降低6℃;又知在距离地面11km以上高空,气温几乎不变。若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃)(1)、写出距地面的高度在11km以内的y与x之间的函数表达式;(2)、上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26℃时,飞机距离地面的高度为7km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12km时,飞机外的气温。26. 已知抛物线L:y=x2+x-6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)、求A、B、C三点的坐标,并求出△ABC的面积;(2)、将抛物线向左或向右平移,得到抛物线L´,且L´与x轴相交于A´、B´两点(点A´在点B´的左侧),并与y轴交于点C´,要使△A´B´C´和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.
(1)、求y与x之间的函数关系式;(2)、当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?25. 根据记录,从地面向上11km以内,每升高1km,气温降低6℃;又知在距离地面11km以上高空,气温几乎不变。若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃)(1)、写出距地面的高度在11km以内的y与x之间的函数表达式;(2)、上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26℃时,飞机距离地面的高度为7km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12km时,飞机外的气温。26. 已知抛物线L:y=x2+x-6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)、求A、B、C三点的坐标,并求出△ABC的面积;(2)、将抛物线向左或向右平移,得到抛物线L´,且L´与x轴相交于A´、B´两点(点A´在点B´的左侧),并与y轴交于点C´,要使△A´B´C´和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.
27. 疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购20000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买 、 、 三种型号的口罩,这三种型号口罩单价如表所示:型号
单价(元/袋)
30
35
40
若购买 型口罩的数量是 型的2倍,设购买 型口罩 袋,该企业购买口罩的总费用为 元.
(1)、请求出 与 的函数关系式;(2)、已知口罩生产厂家能提供的 型口罩的数量不大于 型口罩的数量,当购买 型口罩多少袋时购买口罩的总费用最少?并求最少总费用.28. 为全面落实乡村振兴总要求,充分发扬“为民服务孺子牛”“创新发展拓荒牛”“艰苦奋斗老黄牛”精神,某镇政府计划在该镇试种植苹果树和桔子树共100棵.已知平均每棵果树的投入成本和产量如表所示,且苹果的售价为10元/kg,桔子的售价为6元/kg.成本(元/棵)
产量(kg/棵)
苹果树
120
30
桔子树
80
25
设种植苹果树x棵.
(1)、若种植苹果树和桔子树共获利y元,求y与x之间的函数关系式;(2)、若种植苹果树45棵,求种植苹果树和桔子树共获利多少元?29. 西银高铁于2020年12月26日正式开通运营,从“千年古都”到“塞上江南”,由原来的14个小时变为3小时,沿途风景如画,尽显西北风情.试运行期间,一列动车从西安开往银川,到达目的地后停留一段时间,以原速返回西安,设动车从西安出发x(h),动车离西安的距离为y(km),y与x的函数关系如图所示. (1)、求返回西安时y与x之间的函数关系式;(2)、求动车从西安出发5小时后离西安的距离.30. 已知抛物线 :y= 经过点M(2,﹣3),与y轴交于点C(0,﹣3).(1)、求抛物线 的表达式;(2)、平移抛物线 ,设平移后的抛物线为 ,抛物线 的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?31. 打车软件的出现很大程度上方便了我们的生活,其中“滴漓出行”是全球最大的站式多样化出行渠道,现了解到某市“滴滴快车”普通时段的最新收费标准见下表;
(1)、求返回西安时y与x之间的函数关系式;(2)、求动车从西安出发5小时后离西安的距离.30. 已知抛物线 :y= 经过点M(2,﹣3),与y轴交于点C(0,﹣3).(1)、求抛物线 的表达式;(2)、平移抛物线 ,设平移后的抛物线为 ,抛物线 的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?31. 打车软件的出现很大程度上方便了我们的生活,其中“滴漓出行”是全球最大的站式多样化出行渠道,现了解到某市“滴滴快车”普通时段的最新收费标准见下表;里程/千米
收费/元
2千米以下(含2千米)
11.4
2千米以上,每增加1千米
1.95
(1)、求“滴滴快车”的收费y(元)与行驶的里程数x(千米)之间的函数关系式;(2)、上周一,李老师乘坐“滴滴快车”从家到学校的车费是15.3元,李老师家距离学校多少千米?已知王老师家距离学校1.8千米,求王老师乘坐“滴滴快车”从家到学校的车费.32. 在平面直角坐标系中,抛物线 经过点 和 ,且它的对称轴为直线l.(1)、求该抛物线的表达式;(2)、将抛物线 沿直线l向下平移1个单位长度,得到新抛物线,设新抛物线与y轴的交点为M,直线l与x轴交于点N,动点R在直线l上,在新抛物线上是否存在点Q,使以点N,Q,R为顶点的三角形与 全等?若存在,求符合条件的点Q的坐标;若不存在,请说明理由.33. 某单位计划周末组织员工去周边的某景点旅游,旅行社提供了以下收费方案:当旅游人数不超过10人时,人均费用为240元;当旅游人数超过10人但不超过25人时,与10人相比,每增加1人,人均费用降低6元;当旅游人数超过25人时,人均费用为150元.设参加旅游的人数为x人,人均费用为y元.(1)、求y与x的函数关系式;(2)、如果该公司这次参加旅游的人数有20人,那么总共需要支付给旅行社共多少元?34. 如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.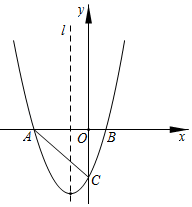 (1)、求该抛物线的表达式;(2)、P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.35. 在平面直角坐标系中,已知抛物线L: 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为 .
(1)、求该抛物线的表达式;(2)、P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.35. 在平面直角坐标系中,已知抛物线L: 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为 . (1)、求抛物线L的表达式;(2)、点P在抛物线 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.36. 如图,在平面直角坐标系中,抛物线 与 轴交于 、 两点(点 在点 的左侧),与 轴交于点 ,点 的坐标为 ,抛物线的对称轴是直线 ,且经过 、 两点的直线 .
(1)、求抛物线L的表达式;(2)、点P在抛物线 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.36. 如图,在平面直角坐标系中,抛物线 与 轴交于 、 两点(点 在点 的左侧),与 轴交于点 ,点 的坐标为 ,抛物线的对称轴是直线 ,且经过 、 两点的直线 .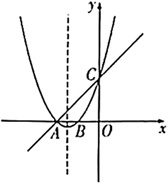 (1)、求抛物线 的函数表达式;(2)、若将抛物线 沿 轴翻折,得到新抛物线 ,抛物线 上是否存在一点 使得 ,若存在,请求出点 的坐标;若不存在,请说明理由.37. 如图,抛物线 与y轴交于点 ,与x轴交于B、C两点,且抛物线的对称轴方程为 .
(1)、求抛物线 的函数表达式;(2)、若将抛物线 沿 轴翻折,得到新抛物线 ,抛物线 上是否存在一点 使得 ,若存在,请求出点 的坐标;若不存在,请说明理由.37. 如图,抛物线 与y轴交于点 ,与x轴交于B、C两点,且抛物线的对称轴方程为 .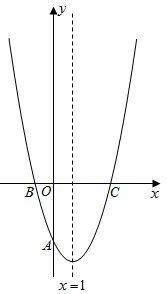 (1)、求抛物线的解析式;(2)、设点P为抛物线对称轴上第一象限内一点,若 的面积为4,求点P的坐标;(3)、点M为抛物线上一点,点N为抛物线的对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时( 为平行四边形的一条边),求此时点M的坐标.38. 在平面直角坐标系中,抛物线L1:y=ax2+bx﹣3a的图象经过点A(﹣1,0)和B(1,4),其关于y轴对称的抛物线L2与x轴交于M、N两点(点N在点M的右侧),与y轴交于点C.(1)、求抛物线L2的表达式;(2)、点D在抛物线L2对称轴上,则在平面直角坐标系中是否存在点E,使得以CN为边,且以点C、N、D、E为顶点的四边形是菱形,若存在,请求出满足条件的点E的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、设点P为抛物线对称轴上第一象限内一点,若 的面积为4,求点P的坐标;(3)、点M为抛物线上一点,点N为抛物线的对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时( 为平行四边形的一条边),求此时点M的坐标.38. 在平面直角坐标系中,抛物线L1:y=ax2+bx﹣3a的图象经过点A(﹣1,0)和B(1,4),其关于y轴对称的抛物线L2与x轴交于M、N两点(点N在点M的右侧),与y轴交于点C.(1)、求抛物线L2的表达式;(2)、点D在抛物线L2对称轴上,则在平面直角坐标系中是否存在点E,使得以CN为边,且以点C、N、D、E为顶点的四边形是菱形,若存在,请求出满足条件的点E的坐标;若不存在,请说明理由.
-