黑龙江省(齐黑大地区)2021年中考数学三模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图是由5个大小相同的小立方体搭成的几何体,主视图和左视图相同的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图是由5个大小相同的小立方体搭成的几何体,主视图和左视图相同的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,CD∥AB,点O在AB上,OE平分 BOD,OF⊥OE, D= ,则 AOF的度数是( )
5. 如图,CD∥AB,点O在AB上,OE平分 BOD,OF⊥OE, D= ,则 AOF的度数是( )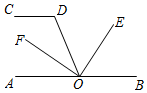 A、 B、 C、 D、6. 如图,电路图上有4个开关和1个小灯泡,同时闭合2个开关,小灯泡发光的概率是( )
A、 B、 C、 D、6. 如图,电路图上有4个开关和1个小灯泡,同时闭合2个开关,小灯泡发光的概率是( ) A、 B、 C、 D、7. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A、 B、 C、 D、7. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )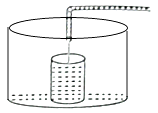 A、
A、 B、
B、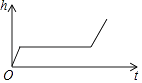 C、
C、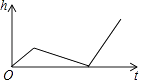 D、
D、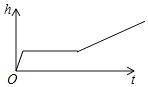 8. 某校5名同学在“国学经典颂读”比赛中,成绩(单位:分)分别是86,95,97,90,88,这组数据的中位数是( )A、97 B、90 C、95 D、889. 社区李主任要用600元钱购买一次性防护服和医用洗手液两种防疫用品,一次性防护服每套40元,医用洗手液每瓶30元,李主任的购买方案共有( )A、3种 B、4种 C、5种 D、6种10. 如图,抛物线 的对称轴是 ,下列结论:① ;② ;③ ;④ ;⑤当 时, .其中结论正确的个数有( )
8. 某校5名同学在“国学经典颂读”比赛中,成绩(单位:分)分别是86,95,97,90,88,这组数据的中位数是( )A、97 B、90 C、95 D、889. 社区李主任要用600元钱购买一次性防护服和医用洗手液两种防疫用品,一次性防护服每套40元,医用洗手液每瓶30元,李主任的购买方案共有( )A、3种 B、4种 C、5种 D、6种10. 如图,抛物线 的对称轴是 ,下列结论:① ;② ;③ ;④ ;⑤当 时, .其中结论正确的个数有( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 根据中国国家统计局4月16日公布的数据显示,中国2021年一季度GDP总量为249310亿元.将249310亿用科学记数法表示为 .12. 如图,四边形 是平行四边形,点 , 在对角线 上,请添加一个条件,使得 ≌ ,那么需要添加的条件是 . (填一个即可)
 13. 如图,在平面直角坐标系中,矩形 的边 ,点 , 分别在 轴、 轴上,反比例函数 的图象经过点 ,则 .
13. 如图,在平面直角坐标系中,矩形 的边 ,点 , 分别在 轴、 轴上,反比例函数 的图象经过点 ,则 . 14. 用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .15. 若关于 的分式方程 无解,则m= .16. 如图,在矩形 中, , ,对角线 , 相交于点 , 为边 上一动点,连接 .若 为等腰三角形,则 的长为 .
14. 用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .15. 若关于 的分式方程 无解,则m= .16. 如图,在矩形 中, , ,对角线 , 相交于点 , 为边 上一动点,连接 .若 为等腰三角形,则 的长为 . 17. 如图,在等腰直角三角形 中, , ,分别连接 , , 的中点,得到第1个等腰直角三角形 ;分别连接 , , 的中点,得到第2个等腰直角三角形 ……以此规律作下去,得到等腰直角三角形 ,则 的长为 .
17. 如图,在等腰直角三角形 中, , ,分别连接 , , 的中点,得到第1个等腰直角三角形 ;分别连接 , , 的中点,得到第2个等腰直角三角形 ……以此规律作下去,得到等腰直角三角形 ,则 的长为 .
三、解答题
-
18.(1)、计算: ;(2)、分解因式: .19. 解方程: .20. 某校研究学生的课余爱好情况,采取抽样调查的方法,从运动、娱乐、阅读、上网四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
 (1)、在这次调查中,共调查了多少名学生?(2)、补全条形统计图;(3)、“阅读”所在扇形的圆心角是多少度?(4)、若该校爱好运动的学生共有800名,则该校学生总数大约有多少名?21. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)、在这次调查中,共调查了多少名学生?(2)、补全条形统计图;(3)、“阅读”所在扇形的圆心角是多少度?(4)、若该校爱好运动的学生共有800名,则该校学生总数大约有多少名?21. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.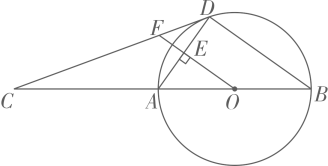 (1)、求证:∠ADC=∠AOF;(2)、若sinC= ,BD=8,求EF的长.22. 2020年新型冠状病毒疫情牵动着全中国人的心,在一条直线上依次有 , , 三个城市, 市在封城后需要大量的物资供应, 市和 市人民积极的向 市送去援助.疫情暴发后,甲、乙两车分别同时从 市和 市出发,载着抗疫物资匀速驶向 市.设甲、乙两车行驶 (单位: )后,与 市的距离分别为 中(单位: ), (单位: ), , 与 的函数关系如图所示.
(1)、求证:∠ADC=∠AOF;(2)、若sinC= ,BD=8,求EF的长.22. 2020年新型冠状病毒疫情牵动着全中国人的心,在一条直线上依次有 , , 三个城市, 市在封城后需要大量的物资供应, 市和 市人民积极的向 市送去援助.疫情暴发后,甲、乙两车分别同时从 市和 市出发,载着抗疫物资匀速驶向 市.设甲、乙两车行驶 (单位: )后,与 市的距离分别为 中(单位: ), (单位: ), , 与 的函数关系如图所示. (1)、a=;(2)、求甲车行驶过程中 与 之间的函数表达式,并写出自变量 的取值范围;(3)、求图中点 的坐标,并写出点 的实际意义;(4)、请直接写出乙车出发多长时间两车相距 .23. 折纸是同学们非常熟悉的手工活动之一,同样一张纸通过不同的折法,可以得出不同的图案.
(1)、a=;(2)、求甲车行驶过程中 与 之间的函数表达式,并写出自变量 的取值范围;(3)、求图中点 的坐标,并写出点 的实际意义;(4)、请直接写出乙车出发多长时间两车相距 .23. 折纸是同学们非常熟悉的手工活动之一,同样一张纸通过不同的折法,可以得出不同的图案.
如图①,在矩形纸片 中, , .
(1)、活动一:如图②,将图①中的矩形纸片 沿过点 的直线折叠,使点 落在 上的点 处,折痕为 ,四边形 是形;
(2)、活动二:如图③,将图①中的矩形纸片 沿直线 折叠,使点 落在 上的点 处,点 不与点 和点 重合,点 落在点 处,连接 ,请猜想四边形 是什么特殊四边形,并证明你的猜想;
(3)、活动三:如图④,将图①中的矩形纸片 沿直线 折叠,使点 的对应点 落在点 处,点 落在点 处,连接 ,四边形 的面积是 ;
(4)、如图⑤,连接图④中的 与 交于点 ,则 .24. 如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点为 ,连接 , , ,直线 与抛物线的对称轴 交于点 . (1)、求抛物线的解析式和直线 的解析式;(2)、求四边形 的面积;(3)、 是第一象限内抛物线上的动点,连接 , ,当 时,求点 的坐标;(4)、在抛物线的对称轴 上是否存在点 ,使得 为等腰三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式和直线 的解析式;(2)、求四边形 的面积;(3)、 是第一象限内抛物线上的动点,连接 , ,当 时,求点 的坐标;(4)、在抛物线的对称轴 上是否存在点 ,使得 为等腰三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.