黑龙江省大庆市2021年中考数学三模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的数是( )A、0 B、 C、5 D、-12. 某自动控制器的芯片,可植入2020000000粒晶体管,这个数字2020000000用科学记数法可表示为A、 B、 C、 D、3. 若 ,则 的值为( )A、6 B、4 C、-4 D、-64. 函数 中自变量 的取值范围是( )A、 B、 C、 D、5. 函数 和 (k1>0,且k1k2<0)的图像大致是( )A、
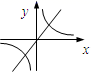 B、
B、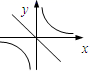 C、
C、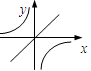 D、
D、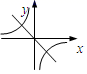 6. 如图为一个正方体的表面展开图,在这个正方体中P、Q、R这三个面所对的面上的数字分别为( )
6. 如图为一个正方体的表面展开图,在这个正方体中P、Q、R这三个面所对的面上的数字分别为( )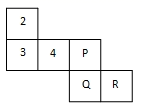 A、2,3,4 B、3,2,4 C、3,4,2 D、以上都不符合题意7. 两组数据:3,a , b , 5与a , 4, 的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为( )A、2 B、3 C、4 D、58. 一个圆柱体和一个圆锥体的底面周长之比是 ,它们的体积比也是 ,圆柱和圆锥的高的比是( )A、1:1 B、3:1 C、1:9 D、1:39. 有长度分别为 的小木棒若干,从中任取三根首尾顺次相接组成三角形,则能组成形状不同的三角形( )A、4种 B、5种 C、6种 D、7种10. 如图,正方形 和等腰直角三角形 ,斜边 与 在一条直线上, 沿射线 方向运动(点E从点D出发),设 与正方形 重叠部分的面积为y . 若 ,则x的值为( )
A、2,3,4 B、3,2,4 C、3,4,2 D、以上都不符合题意7. 两组数据:3,a , b , 5与a , 4, 的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为( )A、2 B、3 C、4 D、58. 一个圆柱体和一个圆锥体的底面周长之比是 ,它们的体积比也是 ,圆柱和圆锥的高的比是( )A、1:1 B、3:1 C、1:9 D、1:39. 有长度分别为 的小木棒若干,从中任取三根首尾顺次相接组成三角形,则能组成形状不同的三角形( )A、4种 B、5种 C、6种 D、7种10. 如图,正方形 和等腰直角三角形 ,斜边 与 在一条直线上, 沿射线 方向运动(点E从点D出发),设 与正方形 重叠部分的面积为y . 若 ,则x的值为( )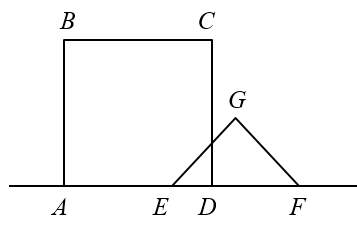 A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或二、填空题
-
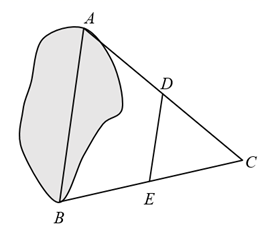
11. 在平面直角坐标系中,点 关于y轴对称的点在第象限.12. 因式分解: .13. 如图,为测量池塘两端A , B两点间的距离,小明先在地上取一个可以直接到达A , B的点C , 并找到 的中点D , E , 并且测出 的长为 ,则A , B间的距离为 .
 14. 如图,一块直角三角板的 角的顶点A与直角顶点C分别在两平行线 上,斜边 平分 ,交直线 于点E , 则 的度数为 .
14. 如图,一块直角三角板的 角的顶点A与直角顶点C分别在两平行线 上,斜边 平分 ,交直线 于点E , 则 的度数为 .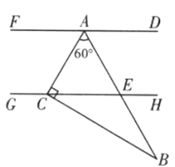 15. 一个质地均匀的小正方体,六个面分别标有数字“1”、“2”、“3”、“4”、“5”、“6”,掷一次小正方体后,观察朝上一面的数字出现偶数的概率是 .16. 如图,下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第1个图中一共有4个小圆圈,第2个图中一共有10个小圆圈第3个图中一共有19个小圆圈……按此规律排列下去,第7个图中小圆圈的个数为个.
15. 一个质地均匀的小正方体,六个面分别标有数字“1”、“2”、“3”、“4”、“5”、“6”,掷一次小正方体后,观察朝上一面的数字出现偶数的概率是 .16. 如图,下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第1个图中一共有4个小圆圈,第2个图中一共有10个小圆圈第3个图中一共有19个小圆圈……按此规律排列下去,第7个图中小圆圈的个数为个.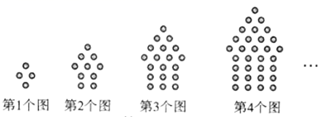 17. 若关于x的一元二次方程 各项系数满足 ,则此方程的根的情况:①必有两个不相等的实数根;②当 时,有两个相等的实数根;③当a , c同号时,方程有两个正的实数根;④当a , b同号时,方程有两个异号实数根.其中结论正确的个数是个.18. 如图,已知在扇形 中, ,半径 .P为弧 上的动点,过点P作 于点M , 于点N , 点M , N分别在半径 上,连接 .点D是 的外心,则点D运动的路径长为 .
17. 若关于x的一元二次方程 各项系数满足 ,则此方程的根的情况:①必有两个不相等的实数根;②当 时,有两个相等的实数根;③当a , c同号时,方程有两个正的实数根;④当a , b同号时,方程有两个异号实数根.其中结论正确的个数是个.18. 如图,已知在扇形 中, ,半径 .P为弧 上的动点,过点P作 于点M , 于点N , 点M , N分别在半径 上,连接 .点D是 的外心,则点D运动的路径长为 .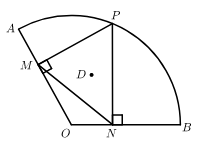
三、解答题
-
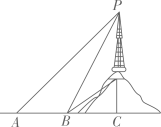
19. 计算: .20. 先化简再求值:(2x+3)(2x-3)-4x(x-1)-(x-2)2 , 其中x=2.21. 解分式方程: .22. 某市为了加快5G网络信号覆盖,在市区附近小山顶架设信号发射塔,如图所示.小军为了知道发射塔的高度,从地面上的一点A测得发射塔顶端P点的仰角是45°,向前走60米到达B点测得P点的仰角是60°,测得发射塔底部Q点的仰角是30°.请你帮小军计算出信号发射塔PQ的高度.(结果精确到0.1 米, )
 23. 为改善民生;提高城市活力,某市有序推行“地摊经济”政策.某社区志愿者随机抽取该社区部分居民,按四个类别:A表示“非常支持”,B表示“支持”,C表示“不关心”,D表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如下两幅不完整的统计图.根据图中提供的信息,解决下列问题:
23. 为改善民生;提高城市活力,某市有序推行“地摊经济”政策.某社区志愿者随机抽取该社区部分居民,按四个类别:A表示“非常支持”,B表示“支持”,C表示“不关心”,D表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如下两幅不完整的统计图.根据图中提供的信息,解决下列问题:
 (1)、这次共抽取了名居民进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是;(2)、将条形统计图补充完整;(3)、该社区共有2000名居民,估计该社区表示“支持”的B类居民大约有多少人?24. 如图,正方形 中,P是对角线 上的一个动点(不与点A , C重合),连接 ,将 绕点B顺时针旋转 得到 ,连接 交 于点E , 的延长线与 交于点F .
(1)、这次共抽取了名居民进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是;(2)、将条形统计图补充完整;(3)、该社区共有2000名居民,估计该社区表示“支持”的B类居民大约有多少人?24. 如图,正方形 中,P是对角线 上的一个动点(不与点A , C重合),连接 ,将 绕点B顺时针旋转 得到 ,连接 交 于点E , 的延长线与 交于点F .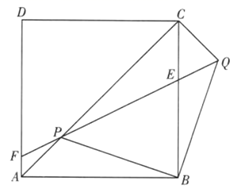 (1)、连接 ,求证 ;(2)、若 ,求 的值.25. 我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格贵150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示;(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受八折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.26. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.
(1)、连接 ,求证 ;(2)、若 ,求 的值.25. 我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格贵150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示;(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受八折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.26. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.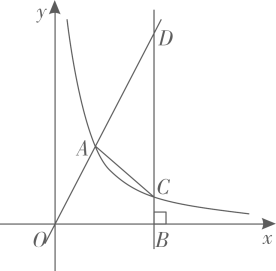 (1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.27. 如图, 与 的边 相切于点C , 与 分别交于点D , E , 是 的直径,过点A作 交 于M , N两点(点M在线段 上).
(1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.27. 如图, 与 的边 相切于点C , 与 分别交于点D , E , 是 的直径,过点A作 交 于M , N两点(点M在线段 上).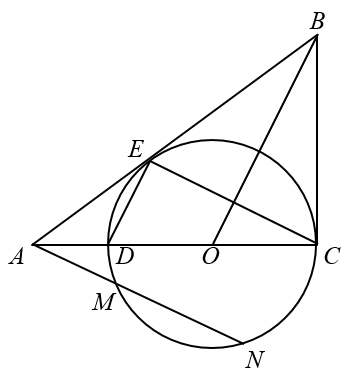 (1)、求证:直线 与 相切;(2)、求证: ;(3)、若 ,求 的长.28. 如图,抛物线 的顶点为A , 与y轴交于点B , 异于顶点A的点 在该抛物线上.
(1)、求证:直线 与 相切;(2)、求证: ;(3)、若 ,求 的长.28. 如图,抛物线 的顶点为A , 与y轴交于点B , 异于顶点A的点 在该抛物线上.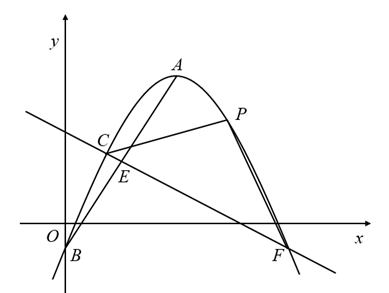 (1)、当 ,且点A在第一象限时,求抛物线的解析式;(2)、在(1)的条件下,连接 ,E为 的中点,直线 与抛物线交于另一点F , P为直线 上方抛物线上的一个动点,设点P的横坐标为t , 当t为何值时, 的面积最大?并求出 面积的最大值;(3)、作直线 与y轴相交于点D . 当点B在x轴上方,且在线段 上时,请直接写出m的取值范围.
(1)、当 ,且点A在第一象限时,求抛物线的解析式;(2)、在(1)的条件下,连接 ,E为 的中点,直线 与抛物线交于另一点F , P为直线 上方抛物线上的一个动点,设点P的横坐标为t , 当t为何值时, 的面积最大?并求出 面积的最大值;(3)、作直线 与y轴相交于点D . 当点B在x轴上方,且在线段 上时,请直接写出m的取值范围.