河北省唐山市路北区2021年中考数学二模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 如图,数轴上点A、B、C、D表示的数中,表示互为相反数的两个点是( )
 A、点B和点C B、点A和点C C、点B和点D D、点A和点D2. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、
A、点B和点C B、点A和点C C、点B和点D D、点A和点D2. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、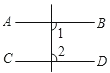 B、
B、 C、
C、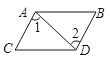 D、
D、 3. 用简便方法计算,将98×102变形正确的是( )A、98×102=1002+22 B、98×102=(100﹣2)2 C、98×102=1002﹣22 D、98×102=(100+2)24. 一个整数 用科学记数法表示为 ,用原数中“ ”的个数(含小数点前的0)为( )A、7 B、8 C、9 D、105. 如果不等式组 恰有 个整数解,则a的取值范围是( )A、 B、 C、 D、6. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的概率是( )
3. 用简便方法计算,将98×102变形正确的是( )A、98×102=1002+22 B、98×102=(100﹣2)2 C、98×102=1002﹣22 D、98×102=(100+2)24. 一个整数 用科学记数法表示为 ,用原数中“ ”的个数(含小数点前的0)为( )A、7 B、8 C、9 D、105. 如果不等式组 恰有 个整数解,则a的取值范围是( )A、 B、 C、 D、6. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的概率是( ) A、 B、 C、 D、7. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
A、 B、 C、 D、7. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,在平面直角坐标系xOy中,点A从(3,4)出发,绕点O顺时针旋转一周,则点A不经过( )
8. 如图,在平面直角坐标系xOy中,点A从(3,4)出发,绕点O顺时针旋转一周,则点A不经过( )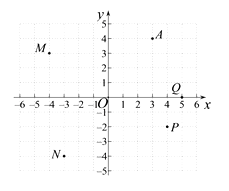 A、点M B、点N C、点P D、点Q9. 如图,快艇从点A处向正北方向航行到B处时,向右转60°航行到C处,再向左转40°继续航行,此时的航行方向在点C的( )
A、点M B、点N C、点P D、点Q9. 如图,快艇从点A处向正北方向航行到B处时,向右转60°航行到C处,再向左转40°继续航行,此时的航行方向在点C的( ) A、北偏东20° B、北偏西20° C、北偏东40° D、北偏西40°10. 求证:直角三角形斜边上中线等于斜边的一半.
A、北偏东20° B、北偏西20° C、北偏东40° D、北偏西40°10. 求证:直角三角形斜边上中线等于斜边的一半.已知:如图,在 中, ,点 是 的中点.求证: .
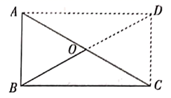
证明:延长 到 ,使 ,
连接 、
中间的证明过程排乱了:
①∵ ②∵ , ;③∴四边形 是平行四边形;④∴四边形 是矩形.
∴ ,∴ .
则中间证明过程正确的顺序是( ).
A、①④②③ B、①③②④ C、②④①③ D、②③①④11. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )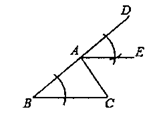 A、∠DAE=∠B B、∠EAC=∠C C、AE∥BC D、∠DAE=∠EAC12. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、∠DAE=∠B B、∠EAC=∠C C、AE∥BC D、∠DAE=∠EAC12. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )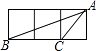 A、
A、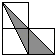 B、
B、 C、
C、 D、
D、 13. 如图,抛物线 的对称轴为直线 ,若关于 的一元二次方程 ( 为实数)在 的范围内有解,则 的取值错误的是( )
13. 如图,抛物线 的对称轴为直线 ,若关于 的一元二次方程 ( 为实数)在 的范围内有解,则 的取值错误的是( )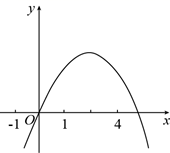 A、 B、 C、 D、14. 如图,若干全等正五边形排成形状,图中所示的是前3个正五边形,则要完成这一圆环还需这样的正五边形( )
A、 B、 C、 D、14. 如图,若干全等正五边形排成形状,图中所示的是前3个正五边形,则要完成这一圆环还需这样的正五边形( )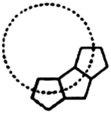 A、6个 B、7个 C、9个 D、10个15. 甲、乙两地相距 ,提速前动车的速度为 ,提速后动车的速度是提速前的 倍,提速后行车时间比提速前减少 ,则可列方程为( )A、 B、 C、 D、16. 如图,在 中, , , ,以边 的中点 为圆心,作半圆与 相切,点 , 分别是边 和半圆上的动点,连接 ,则 长的最大值与最小值的和是( )
A、6个 B、7个 C、9个 D、10个15. 甲、乙两地相距 ,提速前动车的速度为 ,提速后动车的速度是提速前的 倍,提速后行车时间比提速前减少 ,则可列方程为( )A、 B、 C、 D、16. 如图,在 中, , , ,以边 的中点 为圆心,作半圆与 相切,点 , 分别是边 和半圆上的动点,连接 ,则 长的最大值与最小值的和是( ) A、6 B、 C、 D、9
A、6 B、 C、 D、9二、填空题
-
17. 若实数a、b满足|a+2|+ =0,则 = .18. 如图,在平面直角坐标系 中,直线 与 轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接 ,若 .
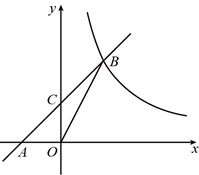 (1)、反比例函数的解析式为;(2)、若直线 与 轴的交点为 ,则 的面积为 .19. 如图, 中, , , , 是 上的动点,将线段 绕点 逆时针旋转 ,得到线段 ,连接 .
(1)、反比例函数的解析式为;(2)、若直线 与 轴的交点为 ,则 的面积为 .19. 如图, 中, , , , 是 上的动点,将线段 绕点 逆时针旋转 ,得到线段 ,连接 .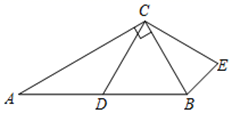 (1)、点 到 的最短距离是;(2)、 的最小值是 .
(1)、点 到 的最短距离是;(2)、 的最小值是 .三、解答题
-
20. 老师课下给同学们留了一个式子: ,让同学自己出题,并写出答案.(1)、小光提出问题:若□代表 ,○代表 ,则计算: ;(2)、小丽提出问题:若 ,当□代表 时,求○所代表的有理数;(3)、小亮提出问题:若 中,若□和○所代表的有理数互为相反数,直接写出□所代表的有理数的取值范围.21. 树兰学校初中部和小学部一起在操场做课间操.初中部排成长方形,每排 人站成 排;小学部排成一个边长 的方阵.(1)、初中部比小学部多多少人?(用字母a,b表示)(2)、当 时,该学校一共有多少名同学?22. 某学校八年级举行了一次数学竞赛,成绩由低到高分为 , , , , 五个等级.竞赛结合后老师随机抽取了部分学生的成绩情况绘制成如下的条形图和扇形图,请根据提供的信息解答以下问题.
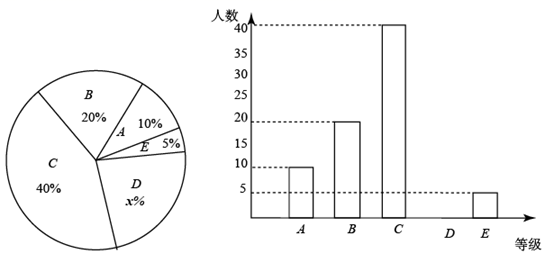 (1)、补全条形统计图.(2)、在本次抽样调查中,成绩的众数和中位数分别处于哪个等级?(3)、成绩为 等级的五个人中有3名男生2名女生,若从中任选两人,利用树状图或列表法求两人恰好是一男一女的概率为多少?23. 已知:如图,点 , , , 在同一直线上, , , .
(1)、补全条形统计图.(2)、在本次抽样调查中,成绩的众数和中位数分别处于哪个等级?(3)、成绩为 等级的五个人中有3名男生2名女生,若从中任选两人,利用树状图或列表法求两人恰好是一男一女的概率为多少?23. 已知:如图,点 , , , 在同一直线上, , , .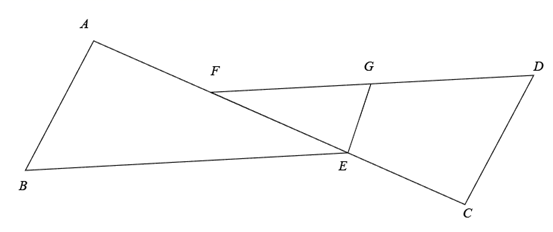 (1)、求证: .(2)、若点 , 分别为线段 , 的中点,连接 ,且 ,求 的长.24. 如图,直线 经过点 和 ,点 的坐标为 , 是线段 上的动点(点 不与点 重合),直线 经过点 ,并与 交于点 .
(1)、求证: .(2)、若点 , 分别为线段 , 的中点,连接 ,且 ,求 的长.24. 如图,直线 经过点 和 ,点 的坐标为 , 是线段 上的动点(点 不与点 重合),直线 经过点 ,并与 交于点 .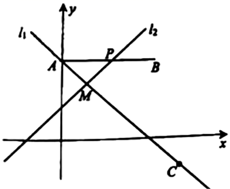 (1)、求 的函数表达式;(2)、当 时,求点 的坐标;(3)、无论 取何值,直线 是否恒经过某点,如是,请直接写出这个点的坐标;如不是,请说明理由;(4)、在 的移动过程中,直接写出 的取值范围.25. 某公司计划生产甲、乙两种产品,公司市场部根据调查后得出:甲种产品所获年利润 (万元)与投入资金 (万元)的平方成正比例;乙种产品所获得年利润 (万元)与投入资金 (万元)成正比例,并得到表格中的数据.设公司计划共投入资金 (万元)( 为常数且 )生产甲、乙两种产品,其中投入甲种产品资金为 (万元)(其中 ),所获全年总利润 (万元)为 与 之和.
(1)、求 的函数表达式;(2)、当 时,求点 的坐标;(3)、无论 取何值,直线 是否恒经过某点,如是,请直接写出这个点的坐标;如不是,请说明理由;(4)、在 的移动过程中,直接写出 的取值范围.25. 某公司计划生产甲、乙两种产品,公司市场部根据调查后得出:甲种产品所获年利润 (万元)与投入资金 (万元)的平方成正比例;乙种产品所获得年利润 (万元)与投入资金 (万元)成正比例,并得到表格中的数据.设公司计划共投入资金 (万元)( 为常数且 )生产甲、乙两种产品,其中投入甲种产品资金为 (万元)(其中 ),所获全年总利润 (万元)为 与 之和.(万元)
2
(万元)
0.1
(万元)
1
(1)、分别求 和 关于 的函数关系式;(2)、求 关于 的函数关系式(用含 的式子表示);(3)、当 时,①公司市场部预判公司全年总利润 的最高值与最低值相差恰好是40万元,请你通过计算说明该预判是否正确;
②公司从全年总利润 中扣除投入甲种产品资金的 倍( )用于其它产品的生产后,得到剩余利润 (万元),若 随 增大而减小,直接写出 的取值范围.
26. 如图,在平行四边形 中, 于 , , ,经过点 作圆 和 边切于 点( 点可与点 、 重合),交 边、 边于 、 . (1)、求 的长;(2)、若点 在边 上,求弧 的长;(3)、若点 与点 重合,判断点 与圆 的位置关系;(4)、设圆 的半径为 ,直接写出 的取值范围.
(1)、求 的长;(2)、若点 在边 上,求弧 的长;(3)、若点 与点 重合,判断点 与圆 的位置关系;(4)、设圆 的半径为 ,直接写出 的取值范围.