广东省肇庆市高要区2021年中考数学二模试卷

试卷更新日期：2021-07-07 类型：中考模拟

进入出卷网下载

一、单选题

1. -2021的绝对值等于（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 函数 $y = \sqrt{x - 2}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x > 2$ D、 $x \geq - 2$

查看试题解析
4. 在九年级体育中考中，某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：46，44，45，42，48，46，47，46.则这组数据的中位数为（）

A、42 B、45 C、46 D、48

查看试题解析
5. 计算 ${(- 1.5)}^{2020} \times {(\frac{2}{3})}^{2021}$ 的结果是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $- \frac{3}{2}$ D、 $- \frac{2}{3}$

查看试题解析
6. 下列运算错误的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{4} \div a = a^{3}$ C、 $\frac{a - b}{b - a} = - 1$ D、 $\frac{1}{c} + \frac{2}{c} = \frac{3}{c}$

查看试题解析
7. 下列一元二次方程有两个相等的实数根的是（）

A、 $x^{2} + 2 x = 0$ B、 $x^{2} - 2 x + 1 = 0$ C、 $x^{2} = 1$ D、 $x^{2} + 1 = 0$

查看试题解析
8. 若双曲线y= $\frac{k - 3}{x}$ 在每一个象限内，y随x的增大而减小，则k的取值范围是（）

A、k＜3 B、k≥3 C、k＞3 D、k≠3

查看试题解析
9. 如图所示，在数轴上表示实数 $\sqrt{13}$ 的点可能是（）

A、点M B、点N C、点P D、点Q

查看试题解析
10. 定义一个新运算，若 $i^{1} = i$ ， $i^{2} = - 1$ ， $i^{3} = - i$ ， $i^{4} = 1$ ， $i^{5} = i$ ， $i^{6} = - 1$ ， $i^{7} = - i$ ， $i^{8} = 1$ ，…，则 $i^{2021}$ 是（）

A、-i B、i C、-1 D、1

查看试题解析

二、填空题

11. “嫦娥一号”卫星顺利进入绕月工作轨道，行程约有1800000千米，1800000这个数用科学记数法可表示为.

查看试题解析
12. 计算： $2 \sin 60 ° - 3 \tan 30 ° =$ ．

查看试题解析
13. 在一个不透明的盒子里装有5个黑色棋子和若干白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是 $\frac{1}{3}$ ，则白色棋子的个数为

查看试题解析
14. 如图，△ABC是⊙O的内接正三角形，图中阴影部分的面积是12π，则⊙O的半径为.

查看试题解析
15. 如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则警示牌的高CD为米.（结果精确到0.1米，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
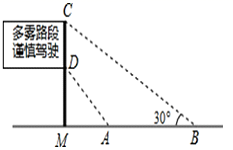16. 如图，把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G ，D、C分别在M 、N的位置上，若∠EFG=52°，则∠2=.

查看试题解析
17. 如图为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象，则下列说法：① $a > 0$ ；② $2 a + b = 0$ ；③ $a + b + c > 0$ ；④当 $- 1 < x < 3$ 时， $y > 0$ ．其中正确的是（填写序号）．

查看试题解析

三、解答题

18. 解不等式组 ${\begin{array}{l} x - 4 < 0 \\ x + 2 (x - 1) \geq 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
19. 先化简，再求值： $\frac{a^{2} - 4}{a - 3} \cdot (1 - \frac{1}{a - 2})$ ，其中 $a = - 3$ ．

查看试题解析
20. 已知△ABC中，∠A＝90°，∠B＝30°．

(1)、作图：作△ABC的高AD交BC于点D（用尺规作图，保留作图痕迹，不写作法）；

(2)、求证：BD＝3CD．

查看试题解析

21. 为了解“停课不停学”期间，学生对线上学习方式的偏好情况，某校随机抽取40名学生进行问卷调查，其统计结果如表：

最喜欢的线上学习方式（每人最多选一种）	人数
直播	10
录播	a
资源包	5
线上答疑	8
合计	40

(1)、a=；

(2)、若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图，求“直播”对应扇形的圆心角度数；

(3)、根据调查结果估计该校1000名学生中，最喜欢“线上答疑”的学生人数；

(4)、在最喜欢“资源包”的学生中，有2名男生，3名女生．现从这5名学生中随机抽取2名学生介绍学习经验，求恰好抽到1名男生和1名女生的概率．

查看试题解析

22. 有一段6000米的道路由甲、乙两个工程队负责完成，已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍，且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天．

(1)、求甲、乙两工程队每天各完成多少米?

(2)、如果甲工程队每天需工程费7000元，乙工程队每天需工程费5000元，若甲队先单独工作若干天，再由甲、乙两工程队合作完成剩余的任务，支付工程队总费用不超过79000元，则两工程队最多可合作施工多少天?（注：工作天数取整数）

查看试题解析
23. 如图，AB是⊙O的直径，AC是弦，OD⊥AC于点D，过点A作⊙O的切线AP，AP与OD的延长线交于点P，连接PC、BC．

(1)、猜想：线段OD与BC有何数量和位置关系，并证明你的结论．

(2)、求证：PC是⊙O的切线.

查看试题解析
24. 如图，在▱ABCD中，点E ， F是直线BD上的两点，DE=BF ．

(1)、求证：四边形AFCE是平行四边形．

(2)、若BD⊥AD ， AB=5，AD=3，四边形AFCE是矩形，求DE的长．

查看试题解析
25. 如图，已知抛物线y=ax²＋bx＋5经过A(－5，0)，B(－4，－3)两点，与x轴的另一个交点为C ，顶点为D ，连接CD ．

(1)、求该抛物线的解析式；

(2)、点P为该抛物线上一动点(与点B ， C不重合)，设点P的横坐标为t ．当点P在直线BC的下方运动时，求△PBC的面积的最大值．

查看试题解析