广东省深圳市罗湖区2021年中考数学三模试卷

试卷更新日期：2021-07-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图所示，数轴上点A所表示的数的绝对值是（）

A、-2 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、2

查看试题解析
2. 下列图形既不是中心对称图形，也不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 据统计，某城市去年接待旅游人数约为89000000人，89000000这个数据用科学记数法表示为（）

A、 $8.9 \times 10^{5}$ B、 $8.9 \times 10^{6}$ C、 $8.9 \times 10^{7}$ D、 $8.9 \times 10^{8}$

查看试题解析
4. 如图，是由四个相同的小正方体组成的几何体，则从正面观察该几何体，得到的形状图是（）

A、 B、 C、 D、

查看试题解析
5. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好是9.4环，方差分别是S_甲²＝0.90，S_乙²＝1.22，S_丙²＝0.45，S_丁²＝1.9，在本次射击测试中，成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 下列运算正确的是（）

A、x³+x³=x⁶ B、a¹²÷a⁴=a³ C、(a³)²=a⁵ D、a⁷·a⁵=a¹²

查看试题解析
7. 如图，已知 $l_{1} // l_{2}$ ，将一个含45°角的三角尺按图中方式放置， $∠ 1 = 24 °$ ，则 $∠ 2$ 的度数为（）

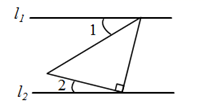A、21° B、24° C、30° D、66°

查看试题解析
8. 如图，用尺规作角平分线，根据作图步骤，在说明射线AN是∠BAC的平分线过程中，以下说法错误的是（）

A、由作弧可知AE＝AF B、由作弧可知FP＝EP C、由SAS 证明△AFP≌△AEP D、由SSS证明△AFP≌△AEP

查看试题解析
9.
函数y=x²+bx+c与y=x的图象如图所示，有以下结论：①b²﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x²+（b﹣1）x+c＜0．其中正确的个数为（　）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，正方形ABCD中，E为AB上一点，AF⊥DE于点F ，已知DF＝5EF＝5，过C、D、F的⊙O与边AD交于点G ，则DG＝（）

A、 $\sqrt{30} - \sqrt{3}$ B、 $\sqrt{30} - 2$ C、 $\sqrt{30} - \sqrt{5}$ D、 $\sqrt{30} - \sqrt{6}$

查看试题解析

二、填空题

11. 因式分解：2x²+xy＝．

查看试题解析
12. 一个不透明的袋子中装有除颜色外完全相同的球共10个，从中随机摸出一个球，若摸到红色球的概率为 $\frac{3}{5}$ ，则袋子中红色球的个数是．

查看试题解析
13. 如图，在△ACB中，∠ACB＝90°，点D为AB的中点，将△ACB绕点C按顺时针方向旋转，当CB经过点D时得到△A₁CB₁ ．若AC＝6，BC＝8，则DB₁的长为．

查看试题解析
14. 如图，已知等边三角形 $A B C$ 的顶点 $A ， B$ 分别在反比例函数 $y = \frac{1}{x}$ 图像的两个分支上，点 $C$ 在反比例函数y= $\frac{k}{x}$ （k≠0）的图像上，当 $Δ A B C$ 的面积最小时，k的值．

查看试题解析
15. 如图，在正方形ABCD中，E是对角线AC上的动点，以DE为边作正方形DEFG，H是CD的中点．连接GH，若GH的最小值是1，则正方形ABCD的边长为．

查看试题解析

三、解答题

16. 计算： $2^{- 1} + \sin 30 ° + \sqrt{8} - {(\sqrt{2} - \tan 60 °)}^{0}$ ．

查看试题解析
17. 解方程：

(1)、 $\frac{6}{x - 1}$ ＝ $\frac{5}{x}$ ；

(2)、x²+6x﹣2＝0．

查看试题解析
18. 为响应党的“文化自信”号召，某校开展了古诗词诵读大赛活动，现随机抽取部分同学的成绩进行统计，并绘制成如下的两个不完整的统计图，请结合图中提供的信息，解答下列各题：

(1)、直接写出a的值，a= ▲ ，并把频数分布直方图补充完整．

(2)、求扇形B的圆心角度数．

(3)、如果全校有2000名学生参加这次活动，90分以上（含90分）为优秀，那么估计获得优秀奖的学生有多少人？

查看试题解析
19. 如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB、连接DO并延长交CB的延长线于点E．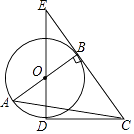

(1)、判断直线CD与⊙O的位置关系，并说明理由；

(2)、若BE=4，DE=8，求AC的长．

查看试题解析
20. 某学校为丰富同学们的课余生活，购买了一批数量相等的象棋和围棋供兴趣小组使用，其中购买象棋用了210元，购买围棋用了378元，已知每副围棋比每副象棋贵8元．

(1)、求每副围棋和象棋各是多少元？

(2)、若该校决定再次购买同种围棋和象棋共50副，且再次购买的费用不超过600元，则该校最多可再购买多少副围棋？

查看试题解析
21. 如图，抛物线y＝﹣x²+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C ．

(1)、直接写出抛物线的解析式：；

(2)、点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E ，交BC于点F ，过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H ，设点D的横坐标为m ．
①求DF+ $\sqrt{2}$ HF的最大值；

②连接EG ，若∠GEH＝45°时，求m的值．

查看试题解析
22. 在平面直角坐标系中，O为原点，四边形ABCD是矩形，点A（0，2），C（2 $\sqrt{3}$ ，0），点D是对角线AC上一点（不与A、C重合），连接BD ，作DE⊥BD ，交x轴于点E ，以线段DE、DB为邻边作矩形BDEF ．

(1)、是否存在这样的点D ，使得△DEC是等腰三角形？若存在，请求出AD的长；若不存在，请说明理由；

(2)、求证： $\frac{D E}{D B} = \frac{\sqrt{3}}{3}$ ；

(3)、设AD＝x ，矩形BDEF的面积为y ，求y关于x的函数关系式，并求出当x取何值时，y有最小值？

查看试题解析