广东省广州市黄埔区2021年中考数学一模试卷
试卷更新日期:2021-07-07 类型:中考模拟
一、单选题
-
1. 6的相反数为( )A、-6 B、6 C、 D、2. 已知一组数据: 这组数据的众数和中位数分别是( )A、86,86 B、86,82 C、87,82 D、87,863. 在平面直角坐标系中,点 关于y轴对称的点的坐标为( )A、 B、 C、 D、4. 若式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 顺次连接矩形各边中点得到的四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形6. 在平面直角坐标系中,函数 的图象经变换后得到函数 的图象,则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移4个单位 D、向右平移4个单位7. 已知点 在第四象限,则m的取值范围是( )A、 B、 C、 D、8. 如图,小明从A点出发,沿直线前进6米后向左转45°,再沿直线前进6米,又向左转45°照这样走下去,他第一次回到出发点A时,共走路程为( )
 A、60 B、72 C、48 D、369. 如图,在直角三角形纸片 中, , ,点E在边 上,将 沿直线 折叠,点B恰好落在斜边 上的点F处,若 ,则 的长是( )
A、60 B、72 C、48 D、369. 如图,在直角三角形纸片 中, , ,点E在边 上,将 沿直线 折叠,点B恰好落在斜边 上的点F处,若 ,则 的长是( ) A、6 B、 C、 D、10. 如图,抛物线 与y轴交于点C , 与x轴交于点 、点 .下列结论:① ;② ;③ ;④ .正确的有( )
A、6 B、 C、 D、10. 如图,抛物线 与y轴交于点C , 与x轴交于点 、点 .下列结论:① ;② ;③ ;④ .正确的有( )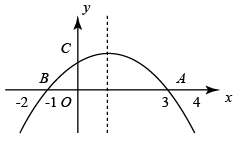 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 分解因式: .12. 如果单项式 与 是同类项,那么 .13. 若 ,则 .14. 若 ,则 的值是 .15. 已知圆锥的底面半径为 ,侧面展开图的圆心角是180°,则圆锥的高是 .16. 如图, 的直径 为6 , , 都是 的半径, ,点P在直径 上移动,则 的最小值为 .

三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 , .19. 某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调名新聘毕业生的专业情况,并将调查结果绘制成如图两幅不完整的统计图,
请根据统计图提供的信息,解答下列问题.
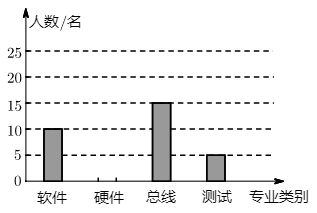
 (1)、 , ;(2)、请补全条形统计图;(3)、在扇形统计图中,“软件”所对应的扇形的圆心角是度;(4)、若该司新招聘600名毕业生,请你估计“总线”专业的毕业生有名.20. 随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G商品生产厂家更新技术后,加快了生产速度,现在每天比更新技术前多生产30万件产品,在生产500万件产品所需时间与更新技术前生产400万件产品所需时间相同,求更新技术前每天生产多少件产品?21. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)、 , ;(2)、请补全条形统计图;(3)、在扇形统计图中,“软件”所对应的扇形的圆心角是度;(4)、若该司新招聘600名毕业生,请你估计“总线”专业的毕业生有名.20. 随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G商品生产厂家更新技术后,加快了生产速度,现在每天比更新技术前多生产30万件产品,在生产500万件产品所需时间与更新技术前生产400万件产品所需时间相同,求更新技术前每天生产多少件产品?21. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.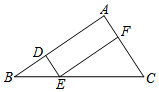 (1)、求证:△BDE∽△EFC.(2)、设 ,
(1)、求证:△BDE∽△EFC.(2)、设 ,①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
22. 如图1所示,点C把线段 分成 与 ,若 ,则称线段 被点C黄金分割(goldensection),点C叫做线段 的黄金分割点, 与 的比叫做黄金比.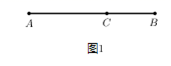 (1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C .
(1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C . (3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.23. 如图,平行四边形 的顶点A在x轴的正半轴上,顶点B的坐标为 ,点D在边 上,已知三角形 的面积是 ,反比例通数 的图象经过C、D两点.
(3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.23. 如图,平行四边形 的顶点A在x轴的正半轴上,顶点B的坐标为 ,点D在边 上,已知三角形 的面积是 ,反比例通数 的图象经过C、D两点. (1)、求点C的坐标;(2)、求点D的横坐标.24. 如图1,在平面直角坐标系中,已知抛物线 与x轴交于 , 两点,与y轴交于点C .
(1)、求点C的坐标;(2)、求点D的横坐标.24. 如图1,在平面直角坐标系中,已知抛物线 与x轴交于 , 两点,与y轴交于点C .

 (1)、求抛物线的二次函数解析式:(2)、若点P在抛物线上,点Q在x轴上,当以点B、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;(3)、如图2,点H是直线 下方抛物线上的动点,连接 , ,当 的面积最大时,求点H的坐标.25. 如图1,正方形 的对角线相交于点O , 延长 到点G , 延长 到点E , 使 , ,以 , 为临边做正方形 ,连接 , .
(1)、求抛物线的二次函数解析式:(2)、若点P在抛物线上,点Q在x轴上,当以点B、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;(3)、如图2,点H是直线 下方抛物线上的动点,连接 , ,当 的面积最大时,求点H的坐标.25. 如图1,正方形 的对角线相交于点O , 延长 到点G , 延长 到点E , 使 , ,以 , 为临边做正方形 ,连接 , . (1)、探究 与 的位置关系与数量关系,并证明;(2)、固定正方形 ,以点O为旋转中心,将图1中的方形 逆时针转n°( )得到正方形 ,如图2,
(1)、探究 与 的位置关系与数量关系,并证明;(2)、固定正方形 ,以点O为旋转中心,将图1中的方形 逆时针转n°( )得到正方形 ,如图2,①在旋转过程中,当 时,求n的值;
②在旋转过程中,设点 到直线 的距离为d , 若正方形 的边长为1,请直接写出d的最大值与最小值,不必说明理由.