辽宁省大连市“八区联考”2021年中考数学二模试卷

试卷更新日期：2021-07-07 类型：中考模拟

进入出卷网下载

一、单选题

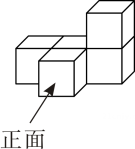
1. 如图是由5个相同的小正方体组成的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 下列四个数中，比－1小的数是（）

A、 $- \frac{3}{2}$ B、 $- \frac{1}{3}$ C、0 D、1

查看试题解析
3. 平面直角坐标系中，点P（a ， 1）与点Q（3，b）关于x轴对称，则a的值是（）

A、1 B、－1 C、3 D、－3

查看试题解析
4. 下列运算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $a^{3} \cdot a^{3} = 2 a^{3}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 ${(- 2 a)}^{2} = 4 a^{2}$

查看试题解析
5. 将一块含45°角的直角三角尺ABC按照如图所示的方式放置，点C落在直线a上，点B落在直线b上，a∥b ， ∠1＝25°，则∠2的度数是（）

A、15° B、20° C、25° D、30°

查看试题解析
6. 下列计算正确的是（）

A、 $2^{0} = 0$ B、 ${(\sqrt{2} + 1)}^{2} = 3$ C、 $\sqrt[3]{- 8} = 2$ D、 $\sqrt{\frac{4}{3}} = \frac{2 \sqrt{3}}{3}$

查看试题解析

7. 某校组织七年级新生测试，抽查了部分学生每分钟跳绳次数（单位：次）．将所得数据统计如下（每组只含最低值，不含最高值）：

组别	第一组	第二组	第三组	第四组	第五组
组别	70~90	90~110	110~130	130~150	150~170
人数	5	13	17	12	3

该样本的中位数落在（）

A、第二组 B、第三组 C、第四组 D、第五组

查看试题解析

8. 如图，将△ABC绕点A逆时针旋转得到 $△ A B^{'} C^{'}$ ，点C的对应点为点 $C^{'}$ ， $C^{'} B^{'}$ 的延长线交BC于点D ，连接AD ．则下列说法错误的是（）

A、 $△ A B C ≅ △ A B^{'} C^{'}$ B、 $A B^{'} / / B C$ C、 $∠ C D C^{'} = ∠ C A C^{'}$ D、AD平分 $∠ B D B^{'}$

查看试题解析
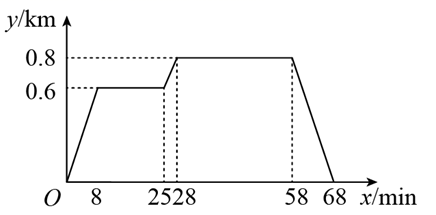
9. 如图，矩形ABCD中，对角线AC ， BD交于点O ， ∠AOD＝60°，AD＝2，则矩形ABCD的面积是（）

A、2 B、 $2 \sqrt{3}$ C、 $4 \sqrt{3}$ D、8

查看试题解析
10. 小明家、食堂、图书馆在同一条直线上，且食堂在小明家和图书馆之间．小明先从家出发去食堂吃早餐，接着去图书馆看报，然后回家，所示图象反映了这个过程中，小明离家的距离y（km）与时间x（min）之间的对应关系．由此给出下列说法：
①小明家与食堂相距0.6km，小明从家去食堂用时8min．②食堂与图书馆相距0.2km．③小明从图书馆回家的速度是0.08 km/min．其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 分式 $\frac{2}{3 x}$ 有意义，则x的取值范围是．

查看试题解析
12. “无风才到地，有风还满空”，柳絮因其纤细轻灵，随风而舞，变化多端，据测定，柳絮纤维的直径约为0.0000105m ，该数值用科学记数法表示为．

查看试题解析
13. 小红参加学校举办的“我爱我的祖国”主题演讲比赛，她的演讲稿、语言表达、形象风度得分分别为85分，70分，80分，若依次按照40%，30%，30%的百分比确定成绩，则她的平均成绩是分．

查看试题解析
14. 《九章算术》内容丰富，与实际生活联系紧密，在书上讲述了这样一个问题：
“今有垣高一丈．倚木于垣，上与垣齐．引木却行一尺，其木至地．问木长几何？”其内容可以表述为：“有一面墙，高1丈．将一根木杆斜靠在墙上，使木杆的上端与墙的上端对齐，下端落在地面上．如果使木杆下端从此时的位置向远离墙的方向移动1尺，则木杆上端恰好沿着墙滑落到地面上．问木杆长多少尺？”（说明：1丈=10尺）

设木杆长 $x$ 尺，依题意，列方程是．

查看试题解析
15. 如图，点A（0，1），平行于x轴的直线AC分别交抛物线 $y_{1} = x^{2} (x \geq 0)$ 与 $y_{2} = \frac{1}{4} x^{2}$ （x≥0）于B、C两点，过点C作y轴的平行线交 $y_{1}$ 于点D ，直线DE∥AC ，交 $y_{2}$ 于点E ，则DE＝．

查看试题解析
16. △ABC内接于⊙O ， AB是⊙O的直径，D是 $\overset{⌢}{B C}$ 的中点，连接BD ， CD ， AB＝2，AC＝x ， CD＝y ，当0＜x＜2时，y关于x的函数解析式为．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 3 - 2 x \leq x + 11 \\ \frac{2 x + 5}{3} - 1 < 2 - x \end{array}$

查看试题解析
18. 甲口袋中有1个红球和1个黄球，乙口袋中有1个红球、1个黄球和1个绿球，这些球除颜色外都相同．

(1)、从乙口袋中随机取一个球，取出的球是红色的概率是．

(2)、从两个口袋中各随机取一个球，求取出的两个球是一红和一黄的概率．

查看试题解析
19. 如图，点A ， F ， E ， D在一条直线上，AF＝DE ， CF∥BE ， AB∥CD ．求证BE＝CF ．

查看试题解析
20. 新冠肺炎防疫工作中，某公司购买了A、B两种不同型号的口罩，已知A型口罩的单价比B型口罩的单价少0.3元，且用4500元购买A型口罩的数量与用6000元购买B型口罩的数量相同．

(1)、A、B两种型号口罩的单价各是多少元？

(2)、根据疫情发展情况，该公司需要增加购买一些口罩，增加购买B型口罩数量是A型口罩数量的2倍，若总费用不超过4950元，则增加购买A型口罩的数量最多是多少个？

查看试题解析
21. 如图，一艘海轮船位于灯塔P北偏东60°方向，与灯塔距离为80n mile的A处，它沿正南方向航行一段时间后，到达位于灯塔P南偏东37°方向的B处，求此时轮船所在B处与灯塔P的距离．（参考数据： $\sin 37^{\circ} \approx 0.6 ， \cos 37^{\circ} \approx 0.8 ， \tan 37^{\circ} \approx 0.75 ， \sqrt{3} \approx 1.7$ ，结果取整数）

查看试题解析
22. 如图，AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，BD⊥CD ， DB的延长线与⊙O交于点E ．

(1)、求证：∠ABE＝2∠A；

(2)、tanA＝ $\frac{1}{2}$ ，BD＝1，求BE的长．

查看试题解析
23. 如图，平面直角坐标系中，点C在x轴上，点A的横坐标是1，以OA ， OC为邻边作 $▱ A B C O$ ，点D是BC的中点，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点A ，点D ．

(1)、求点B的坐标（用含k的代数式表示）；

(2)、连接AD ，若AB＝AD ，求k的值．

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = - \frac{4}{3} x + 4$ 与坐标轴分别交于点A和点B ，直线y＝x与AB交于点C ，点P从点A出发，沿边AO $\to$ OC向终点C运动，过点P作y轴的垂线，交线段AC于点D ．点P在AO上的速度为每秒1个单位长度，在OC上的速度为每秒a个单位长度．设点P的运动时间为t（s），△BPD的面积为S（单位长度²）．

(1)、点C的坐标为；

(2)、当 $t = \frac{33}{7}$ 时，点P到达终点C ，求a的值；

(3)、求S关于t的函数解析式，并直接写出自变量t的取值范围．

查看试题解析
25. 如图，在△ABC中，∠BCA＝90°，点E在BC上，且EC＝AC ．连接AE ， F为AE的中点，CD⊥AB于D ，过点E作EH∥CD交DF的延长线于点H ， DH交BC于M ．

(1)、探究∠EAB和∠BCD之间的数量关系，并证明；

(2)、求证AD＝EH；

(3)、若BC＝k $\cdot$ AC ，求 $\frac{M C}{E B}$ 的值（用含有k的代数式表示）．

查看试题解析
26. 已知函数 $y = {\begin{matrix} 2 x^{2} - 4 m x - 2 m & (x \geq m) \\ - x^{2} - m x - m & (x < m) \end{matrix}$ ，其中m为常数，该函数图象记为F ．

(1)、当m＝1，且－1≤x≤2时，求该函数的最大值；

(2)、当 $\frac{- 1 + \sqrt{3}}{2} \leq m \leq 2$ 时，函数图象F与直线 $y = \frac{1}{2}$ 交于点T ，与直线y＝－1至少有两个交点M、N（点M在左，点N在右），若∠TNM＝135°，求m的值；

(3)、已知矩形ABCD各顶点坐标分别是A（－2m＋1，1），B（－m＋3，1），C（－m＋3，－1），D（－2m＋1，－1），当图象F与矩形ABCD的四边只有两个交点时，求的m的取值范围（直接写出结果）．

查看试题解析