辽宁省本溪市、辽阳、葫芦岛2021年中考数学试卷
试卷更新日期:2021-07-07 类型:中考真卷
一、单选题
-
1. -5的相反数是( )A、 B、 C、5 D、-52. 下列漂亮的图案中似乎包含了一些曲线,其实它们这种神韵是由多条线段呈现出来的,这些图案中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、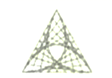 D、
D、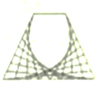 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,该几何体的左视图是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,该几何体的左视图是( )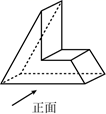 A、
A、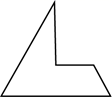 B、
B、 C、
C、 D、
D、 5. 如表是有关企业和世界卫生组织统计的5种新冠疫苗的有效率,则这5种疫苗有效率的中位数是( )
5. 如表是有关企业和世界卫生组织统计的5种新冠疫苗的有效率,则这5种疫苗有效率的中位数是( )疫苗名称
克尔来福
阿斯利康
莫德纳
辉瑞
卫星V
有效率
79%
76%
95%
95%
92%
A、79% B、92% C、95% D、76%6. 反比例函数 的图象分别位于第二、四象限,则直线 不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图为本溪、辽阳6月1日至5日最低气温的折线统计图,由此可知本溪,辽阳两地这5天最低气温波动情况是( )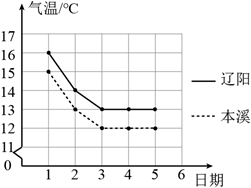 A、本溪波动大 B、辽阳波动大 C、本溪、辽阳波动一样 D、无法比较8. 一副三角板如图所示摆放,若 ,则 的度数是( )
A、本溪波动大 B、辽阳波动大 C、本溪、辽阳波动一样 D、无法比较8. 一副三角板如图所示摆放,若 ,则 的度数是( )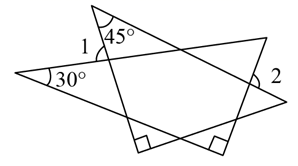 A、80° B、95° C、100° D、110°9. 如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点E , 点F为 的中点,连接 ,若 ,则 的周长为( )
A、80° B、95° C、100° D、110°9. 如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点E , 点F为 的中点,连接 ,若 ,则 的周长为( ) A、 B、 C、 D、410. 如图,在矩形 中, , ,动点P沿折线 运动到点B , 同时动点Q沿折线 运动到点C , 点 在矩形边上的运动速度为每秒1个单位长度,点P , Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒, 的面积为S , 则下列图象能大致反映S与t之间函数关系的是( )
A、 B、 C、 D、410. 如图,在矩形 中, , ,动点P沿折线 运动到点B , 同时动点Q沿折线 运动到点C , 点 在矩形边上的运动速度为每秒1个单位长度,点P , Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒, 的面积为S , 则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、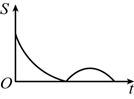
二、填空题
-
11. 若 在实数范围内有意义,则x的取值范围为 .12. 分解因式: .13. 有5张看上去无差别的卡片,上面分别写着 , ,0, ,2,从中随机抽取一张,则抽出卡片上写的数是 的概率为 .14. 若关于x的一元二次方程 有两个相等的实数根,则k的值为 .15. 为了弘扬我国书法艺术,培养学生良好的书写能力,某校举办了书法比赛,学校准备为获奖同学颁奖.在购买奖品时发现,A种奖品的单价比B种奖品的单价多10元,用300元购买A种奖品的数量与用240元购买B种奖品的数量相同.设B种奖品的单价是x元,则可列分式方程为 .16. 如图,由边长为1的小正方形组成的网格中,点A , B , C都在格点上,以 为直径的圆经过点C和点D , 则 .
 17. 如图, 是半圆的直径,C为半圆的中点, , ,反比例函数 的图象经过点C , 则k的值为 .
17. 如图, 是半圆的直径,C为半圆的中点, , ,反比例函数 的图象经过点C , 则k的值为 .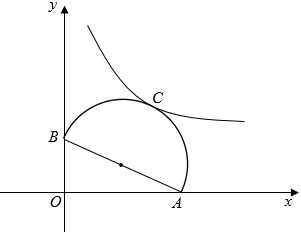 18. 如图,将正方形纸片 沿 折叠,使点C的对称点E落在边 上,点D的对称点为点F , 交 于点G , 连接 交 于点H , 连接 .下列四个结论中:① ;② ;③ 平分 ;④ ,正确的是(填序号即可).
18. 如图,将正方形纸片 沿 折叠,使点C的对称点E落在边 上,点D的对称点为点F , 交 于点G , 连接 交 于点H , 连接 .下列四个结论中:① ;② ;③ 平分 ;④ ,正确的是(填序号即可).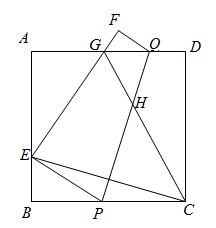
三、解答题
-
19. 先化简,再求值: ,其中 .20. 为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有:A . 回顾重要事件;B . 列举革命先烈;C . 讲述英雄故事;D . 歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题:
 (1)、本次被调查的学生共有名;(2)、在扇形统计图中“B项目”所对应的扇形圆心角的度数为 ▲ ,并把条形统计图补充完整;(3)、从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.21. 某班计划购买两种毕业纪念册,已知购买1本手绘纪念册和4本图片纪念册共需135元,购买5本手绘纪念册和2本图片纪念册共需225元.(1)、求每本手绘纪念册和每本图片纪念册的价格分别为多少元?(2)、该班计划购买手绘纪念册和图片纪念册共40本,总费用不超过1100元,那么最多能购买手绘纪念册多少本?22. 如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道 .无人机从点A的正上方点C , 沿正东方向以 的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
(1)、本次被调查的学生共有名;(2)、在扇形统计图中“B项目”所对应的扇形圆心角的度数为 ▲ ,并把条形统计图补充完整;(3)、从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.21. 某班计划购买两种毕业纪念册,已知购买1本手绘纪念册和4本图片纪念册共需135元,购买5本手绘纪念册和2本图片纪念册共需225元.(1)、求每本手绘纪念册和每本图片纪念册的价格分别为多少元?(2)、该班计划购买手绘纪念册和图片纪念册共40本,总费用不超过1100元,那么最多能购买手绘纪念册多少本?22. 如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道 .无人机从点A的正上方点C , 沿正东方向以 的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
(参考数据: , , , )
(1)、求无人机的高度 (结果保留根号);(2)、求 的长度(结果精确到1m).23. 某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.(1)、请直接写出y(个)与x(元)之间的函数关系式;(2)、当销售单价是多少元时,该网店每星期的销售利润是2400元?(3)、当销售单价是多少元时,该网店每星期的销售利润最大?最大利润是多少元?24. 如图,在 中, ,延长 到点D , 以 为直径作 ,交 的延长线于点E , 延长 到点F , 使 . (1)、求证: 是 的切线;(2)、若 , , ,求 的长.25. 在▱ 中, , 平分 ,交对角线 于点G , 交射线 于点E , 将线段 绕点E顺时针旋转 得线段 .
(1)、求证: 是 的切线;(2)、若 , , ,求 的长.25. 在▱ 中, , 平分 ,交对角线 于点G , 交射线 于点E , 将线段 绕点E顺时针旋转 得线段 . (1)、如图1,当 时,连接 ,请直接写出线段 和线段 的数量关系;(2)、如图2,当 时,过点B作 于点,连接 ,请写出线段 , , 之间的数量关系,并说明理由;(3)、当 时,连接 ,若 ,请直接写出 与 面积的比值.26. 如图,抛物线 与x轴交于点A和点 ,与y轴交于点 ,连接 , ,点P是抛物线第一象限上的一动点,过点P作 轴于点D , 交 于点E .
(1)、如图1,当 时,连接 ,请直接写出线段 和线段 的数量关系;(2)、如图2,当 时,过点B作 于点,连接 ,请写出线段 , , 之间的数量关系,并说明理由;(3)、当 时,连接 ,若 ,请直接写出 与 面积的比值.26. 如图,抛物线 与x轴交于点A和点 ,与y轴交于点 ,连接 , ,点P是抛物线第一象限上的一动点,过点P作 轴于点D , 交 于点E . (1)、求抛物线的解析式;(2)、如图1,作 于点P , 使 ,以 , 为邻边作矩形 .当矩形 的面积是 面积的3倍时,求点P的坐标;(3)、如图2,当点P运动到抛物线的顶点时,点Q在直线 上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
(1)、求抛物线的解析式;(2)、如图1,作 于点P , 使 ,以 , 为邻边作矩形 .当矩形 的面积是 面积的3倍时,求点P的坐标;(3)、如图2,当点P运动到抛物线的顶点时,点Q在直线 上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.