浙江省湖州市吴兴区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-07 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 二次根式 $\sqrt{2 x - 2}$ 在实数范围内有意义，则x的取值范围是（）．

A、x≥0 B、x≥﹣1 C、x≥1 D、x≤﹣1

查看试题解析
2. 用反证法证明“a＞0”时，应假设（）．

A、a＜0 B、a ≤0 C、a ≠0 D、a＝0

查看试题解析
3. 如图，反比例函数y＝ $\frac{k}{x}$ 的图象与直线y＝mx相交于A ， B两点，点B的坐标为（﹣2，﹣3），则点A的坐标为（）.

A、（﹣2，﹣3） B、（2，3） C、（﹣2，3） D、（2，﹣3）

查看试题解析
4. 把n边形变为（n+x）边形，内角和增加了180°，则x的值为（）．

A、1 B、2 C、3 D、4

查看试题解析
5. 4张扑克牌如图1所示放在桌子上，小明将其中一张旋转180°后得到的图如图2所示，那么他旋转的牌从左起是（）．

A、第一张 B、第二张 C、第三张 D、第四张

查看试题解析
6. 一元二次方程x²﹣3x+3＝0的根的情况是（）．

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、不能确定

查看试题解析
7. 在第60届国际数学奥林匹克比赛中，中国队荣获团体总分第一名．我国参赛选手比赛成绩的方差计算公式为：S²＝ $\frac{1}{6} [{(x_{1} - 38)}^{2} + {(x_{2} - 38)}^{2} + ...... + {(x_{6} - 38)}^{2}]$ ，下列说法错误的是（）．

A、我国一共派出了6名选手 B、我国参赛选手的平均成绩为38分 C、我国选手比赛成绩的中位数为38 D、我国选手比赛成绩的团体总分为228分

查看试题解析
8. 如图，四边形ABCD为平行四边形，延长AD到E ，使DE＝AD ，连结EB ， EC ， DB ，添加一个条件，不能使四边形DBCE成为矩形的是（）．

A、AB＝BE B、CE⊥DE C、∠ADB＝90° D、BE⊥AB

查看试题解析
9. 如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数 $y = \frac{k}{x}$ 在第一象限的图象经过点B ，若 $O A^{2} - A B^{2} = 6$ ，则 $k$ 的值为（）．

A、6 B、3 C、 $6 \sqrt{2}$ D、 $3 \sqrt{2}$

查看试题解析
10. 如图，已知四边形ABCD是正方形，点E为对角线AC上一点，连结DE ，过点E作EF⊥DE ，交BC延长线上于点F ，以DE ， EF为邻边作矩形DEFG ，连结CG﹒若AB＝2 $\sqrt{2}$ ，则CE+CG的值为（）.

A、2 B、3 C、4 D、5

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 计算： ${\sqrt{（ - 11 ）^{2}}}^{} =$ ．

查看试题解析
12. 甲、乙、丙、丁四个小组参加体育测试，他们成绩的平均分均为26分，方差分别为：S_甲²＝2.5，S_乙²＝15.7，S_丙²＝9，S_丁²＝11.2，则这四个小组体育测试成绩最稳定的是
组．

查看试题解析
13. 已知点A（x₁ ， y₁），B（x₂ ， y₂）在反比例函数y= $\frac{- a^{2} - 1}{x}$ 的图象上，且x₁＞x₂＞0，则y₁y₂（用不等号填空）.

查看试题解析
14. 近年来某市加大了对教育经费的投入，2018年投入2500万元，2020年将投入3600万元，设该市投入教育经费的年平均增长率为x ，根据题意则可以列出的方程是．

查看试题解析
15. 如图，在平行四边形ABCD中， AE平分∠BAD交BC于点E ，过点E作AE的垂线交CD于点F ，若CF=1，AD=5，则AB= ．

查看试题解析
16. 如图，已知菱形ABCD的对角线AC的中点与坐标原点重合，AF⊥AC交x轴于点F ，反比例函数 $y = \frac{k}{x} (k < 0 ， x < 0)$ 的图象经过点A ，与AF交于点E ，且AE=EF ， △ADF的面积为6，则k的值为．

查看试题解析

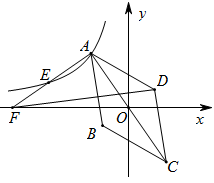
三、解答题（本题有8小题，共66分）

17. 二次根式计算：

(1)、 $2 \sqrt{2} - \sqrt{18} + \sqrt{\frac{1}{2}}$ ．

(2)、 $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) - \sqrt{12} \div \sqrt{3}$ ．

查看试题解析
18. 解下列一元二次方程：

(1)、 $x^{2} - 6 x = 0$

(2)、 $x^{2} - 4 x - 6 = 0$

查看试题解析
19. 如图，在平行四边形ABCD中，AC为其对角线，过点D作AC的平行线与BC的延长线交于点E ．

(1)、求证：△ABC≌△DCE；

(2)、若AC=BC ，求证：四边形ACED为菱形．

查看试题解析
20. 在“慈善一日捐”活动中，为了解某校学生的捐款情况，抽样调查了该校部分学生的捐款数（单位：元），并绘制成如图所示的统计图．

(1)、本次调查的人数是人；

(2)、这组数据的众数为元，中位数为元；

(3)、求这组数据的平均数．

查看试题解析
21. 如图，一次函数y＝x+b的图象分别与x轴，y轴交于点A ，点B ，与反比例函数y＝ $\frac{k}{x}$ 的图象在第一象限交于点C ，若OB＝2，点C的纵坐标为3．

(1)、求反比例函数的解析式；

(2)、求△AOC的面积.

查看试题解析
22. 为了丰富市民的文化生活，我市某景点开放夜游项目．为吸引游客组团来此夜游，特推出了如下门票收费标准：
标准一：如果人数不超过20人，门票价格为60元/人；

标准二：如果人数超过20人，每超过1人，门票价格降低2元，但门票价格不低于50元/人．

(1)、当夜游人数为15人时，人均门票价格为元；当夜游人数为25人时，人均门票价格为元；

(2)、若某单位支付门票费用共1232元，则该单位这次共有多少名员工去此景点夜游？

查看试题解析
23. 如图

如图1，在正方形ABCD中，点P是对角线BD上的一点，连结CP.

(1)、求证：△ADP≌△CDP；

(2)、如图2，延长AP交线段DC于点Q ，交BC的延长线于点G ，点M是GQ的中点，连结CM ．求证：PC⊥MC；

(3)、如图3，延长AP交射线DC于点Q ，交BC于点G ，点M是GQ的中点，连结CM ．若PM=2， ∠BAP=30°.求AB的长.

查看试题解析
24. 如图，在平面直角坐标系中，直线y=-x+5与反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象相交于点A（3，a）和点B（b ， 3），点D ， C分别是x轴和y轴的正半轴上的动点，且满足
CD∥AB.

(1)、求a ， b的值及反比例函数的解析式；

(2)、若OD=1，求点C的坐标，判断四边形ABCD的形状并说明理由；

(3)、若点M是反比例函数y＝ $\frac{k}{x}$ （x＞0）图象上的一个动点，当△AMD是以AM为直角边的等腰直角三角形时，求点M的坐标.

查看试题解析