江苏省盐城市2021年中考数学试卷
试卷更新日期:2021-07-07 类型:中考真卷
一、单选题
-
1. -2021的绝对值是( )A、 B、 C、-2021 D、20212. 计算: 的结果是( )A、 B、 C、 D、3. 北京2022年冬奥会会徽如图所示,组成会徽的四个图案中是轴对称图形的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )
4. 如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )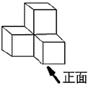 A、
A、 B、
B、 C、
C、 D、
D、 5. 2020年12月30日盐城至南通高速铁路开通运营,盐通高铁总投资约2628000万元,将数据2628000用科学记数法表示为( )A、 B、 C、 D、6. 将一副三角板按如图方式重叠,则 的度数为( )
5. 2020年12月30日盐城至南通高速铁路开通运营,盐通高铁总投资约2628000万元,将数据2628000用科学记数法表示为( )A、 B、 C、 D、6. 将一副三角板按如图方式重叠,则 的度数为( ) A、 B、 C、 D、7. 若 是一元二次方程 的两个根,则 的值是( )A、2 B、-2 C、3 D、-38. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、7. 若 是一元二次方程 的两个根,则 的值是( )A、2 B、-2 C、3 D、-38. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )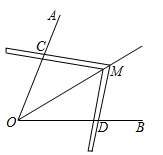 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
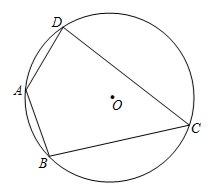
9. 一组数据2,0,2,1,6的众数为.10. 分解因式:a2+2a+1=11. 若一个多边形的每一个外角都等于40°,则这个多边形的边数是 .12. 如图,在⊙O内接四边形 中,若 ,则 .
 13. 如图,在Rt 中, 为斜边 上的中线,若 ,则 .
13. 如图,在Rt 中, 为斜边 上的中线,若 ,则 .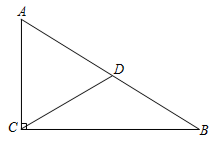 14. 一圆锥的底面半径为2,母线长为3,则这个圆锥的侧面积为.15. 劳动教育己纳入人才培养全过程,某学校加大投入,建设校园农场,该农场一种作物的产量两年内从300千克增加到363千克.设平均每年增产的百分率为 ,则可列方程为.16. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.
14. 一圆锥的底面半径为2,母线长为3,则这个圆锥的侧面积为.15. 劳动教育己纳入人才培养全过程,某学校加大投入,建设校园农场,该农场一种作物的产量两年内从300千克增加到363千克.设平均每年增产的百分率为 ,则可列方程为.16. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.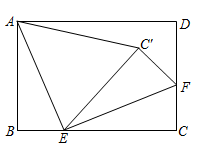
三、解答题
-
17. 计算: .18. 解不等式组:19. 先化简,再求值: ,其中 .20. 已知抛物线 经过点 和 .(1)、求 、 的值;(2)、将该抛物线向上平移2个单位长度,再向右平移1个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式.21. 如图,点 是数轴上表示实数 的点.

(1)用直尺和圆规在数轴上作出表示实数的 的点 ;(保留作图痕迹,不写作法)
(2)利用数轴比较 和 的大小,并说明理由.22. 圆周率 是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对 有过深入的研究.目前,超级计算机已计算出 的小数部分超过31.4万亿位.有学者发现,随着 小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
 (1)、从 的小数部分随机取出一个数字,估计数字是6的概率为;(2)、某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)23. 如图, 、 、 分别是 各边的中点,连接 、 、 .
(1)、从 的小数部分随机取出一个数字,估计数字是6的概率为;(2)、某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)23. 如图, 、 、 分别是 各边的中点,连接 、 、 .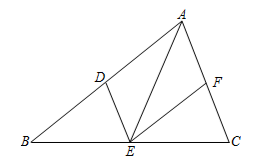 (1)、求证:四边形 为平行四边形;(2)、加上条件 ▲ 后,能使得四边形 为菱形,请从① ;② 平分 ;③ ,这三个条件中选择条件填空(写序号),并加以证明.24. 如图, 为线段 上一点,以 为圆心 长为半径的⊙O交 于点 ,点 在⊙O上,连接 ,满足 .
(1)、求证:四边形 为平行四边形;(2)、加上条件 ▲ 后,能使得四边形 为菱形,请从① ;② 平分 ;③ ,这三个条件中选择条件填空(写序号),并加以证明.24. 如图, 为线段 上一点,以 为圆心 长为半径的⊙O交 于点 ,点 在⊙O上,连接 ,满足 . (1)、求证: 是⊙O的切线;(2)、若 ,求 的值.25. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)、求证: 是⊙O的切线;(2)、若 ,求 的值.25. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .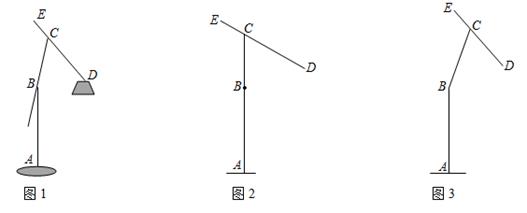 (1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )26. 为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:
(1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )26. 为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:该地区每周接种疫苗人数统计表
周次
第1周
第2周
第3周
第4周
第5周
第6周
第7周
第8周
接种人数(万人)
7
10
12
18
25
29
37
42
该地区全民接种疫苗情况扇形统计图
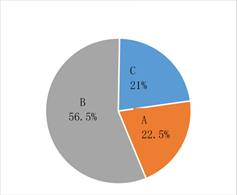
A:建议接种疫苗已接种人群
B:建议接种疫苗尚未接种人群
C:暂不建议接种疫苗人群
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3周开始这些点大致分布在一条直线附近,现过其中两点 、 作一条直线(如图所示,该直线的函数表达式为 ),那么这条直线可近似反映该地区接种人数的变化趋势.
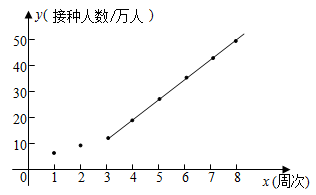
请根据以上信息,解答下列问题:
(1)、这八周中每周接种人数的平均数为万人:该地区的总人口约为万人;(2)、若从第9周开始,每周的接种人数仍符合上述变化趋势.①估计第9周的接种人数约为 ▲ 万人;
②专家表示:疫苗接种率至少达60%,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
(3)、实际上,受疫苗供应等客观因素,从第9周开始接种人数将会逐周减少 万人,为了尽快提高接种率,一旦周接种人数低于20万人时,卫生防疫部门将会采取措施,使得之后每周的接种能力一直维持在20万人.如果 ,那么该地区的建议接种人群最早将于第几周全部完成接种?27. 学习了图形的旋转之后,小明知道,将点 绕着某定点 顺时针旋转一定的角度 ,能得到一个新的点 .经过进一步探究,小明发现,当上述点 在某函数图象上运动时,点 也随之运动,并且点 的运动轨迹能形成一个新的图形.试根据下列各题中所给的定点 的坐标和角度 的大小来解决相关问题.
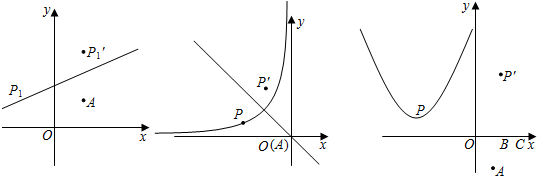 (1)、(初步感知)
(1)、(初步感知)如图1,设 , ,点 是一次函数 图像上的动点,已知该一次函数的图象经过点 .
点 旋转后,得到的点 的坐标为;
(2)、若点 的运动轨迹经过点 ,求原一次函数的表达式.(3)、(深入感悟)如图2,设 , ,点 反比例函数 的图像上的动点,过点 作二、四象限角平分线的垂线,垂足为 ,求 的面积.
(4)、(灵活运用)如图3,设A , ,点 是二次函数 图像上的动点,已知点 、 ,试探究 的面积是否有最小值?若有,求出该最小值;若没有,请说明理由.