江西省重点中学盟校2021届高三理数3月第一次联考试卷
试卷更新日期:2021-07-06 类型:高考模拟
一、单选题
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 的二项展开式中第三项是( )A、 B、160 C、 D、3. 复数z的共轭复数为 , 是z为纯虚数的( )条件A、充要 B、充分不必要 C、必要不充分 D、既不充分也不必要4. 过双曲线 的右焦点F作它的渐近线l的垂线,垂足为P , 若 (O是坐标原点),则 ( )A、 B、2 C、5 D、5. 直三棱柱的侧棱长和底面边长均为2,主视图和俯视图如图所示,则其左视图的面积为( )
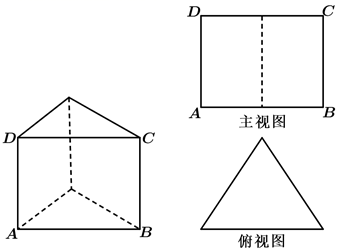 A、2 B、 C、4 D、6. 若函数 在 处取极值0,则 ( )A、0 B、2 C、-2 D、17. 已知直线 和 相切,则 的最大值是( )A、 B、 C、 D、18. 设二元一次不等式组 所表示的平面区域为 ,使函数 ( 且 )的图像过区域 的a的取值范围是( )A、 B、 C、 D、9. 的图像如图所示,下列有关它的描述正确的是( )
A、2 B、 C、4 D、6. 若函数 在 处取极值0,则 ( )A、0 B、2 C、-2 D、17. 已知直线 和 相切,则 的最大值是( )A、 B、 C、 D、18. 设二元一次不等式组 所表示的平面区域为 ,使函数 ( 且 )的图像过区域 的a的取值范围是( )A、 B、 C、 D、9. 的图像如图所示,下列有关它的描述正确的是( )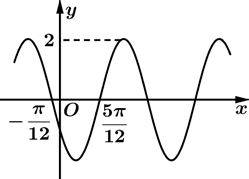 A、 B、把 图像向左平移 单位长度,可得 C、把 图像向右平移 单位长度,可得 D、为得到它的图像可将 的图像向右平移 单位长度,再把所得图像上点的横坐标变为原来的10. 碳-14年代测定法由时任美国芝加哥大学教授威拉得·利比(Willard Frank Libby)发明,威拉得·利比因此获得诺贝尔化学奖.碳是有机物的元素之一,生物在生存的时候,由于需要呼吸,其体内的碳-14含量大致不变,生物死去后会停止呼吸,此时体内的碳-14开始减少,人们可通过检测一件古物的碳-14含量,来估计它的大概年龄,这种方法称之为碳定年法.设 是生物样品中的碳-14的含量, 是活体组织中碳-14的含量,t为生物死亡的时间(单位年),已知 (其中T为碳-14半衰期,且 ),若2021年测定某生物样本中 ,则此生物大概生活在哪个朝代( )
A、 B、把 图像向左平移 单位长度,可得 C、把 图像向右平移 单位长度,可得 D、为得到它的图像可将 的图像向右平移 单位长度,再把所得图像上点的横坐标变为原来的10. 碳-14年代测定法由时任美国芝加哥大学教授威拉得·利比(Willard Frank Libby)发明,威拉得·利比因此获得诺贝尔化学奖.碳是有机物的元素之一,生物在生存的时候,由于需要呼吸,其体内的碳-14含量大致不变,生物死去后会停止呼吸,此时体内的碳-14开始减少,人们可通过检测一件古物的碳-14含量,来估计它的大概年龄,这种方法称之为碳定年法.设 是生物样品中的碳-14的含量, 是活体组织中碳-14的含量,t为生物死亡的时间(单位年),已知 (其中T为碳-14半衰期,且 ),若2021年测定某生物样本中 ,则此生物大概生活在哪个朝代( )参考资料:
西周:公元前1046年—前771年 晋代:公元265—公元420
宋代:公元907—公元1279 明代:公元1368—公元1644
A、西周 B、晋代 C、宋代 D、明代11. 已知圆 与抛物线 交于A , B两点,且 ,则如图所示阴影部分绕x轴旋转形成的旋转体的体积是( )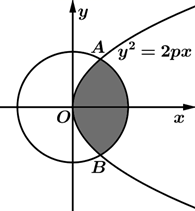 A、 B、 C、 D、12. 数列 中 表示与 最接近的整数,则 ( )A、 B、 C、 D、
A、 B、 C、 D、12. 数列 中 表示与 最接近的整数,则 ( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , ,若 ,则 .14. 数列 前n项和为 ,且满足 , ,则 .15. 已知某农场某植物高度 ,且 ,如果这个农场有这种植物10000棵,试估计该农场这种植物高度在区间 上的棵数为.
参考数据:若 ,则 , , .
16. 在 中,角A , B , C的对边分别为a , b , c , , , ,则 .三、解答题
-
17. 首项为2的等差数列 ,满足 , , 成等比数列,且 .(1)、求 的通项公式;(2)、记数列 的前n项和为 ,若 ,求n的值.18. 如图已知四棱台 的上底面和下底面都是正方形,且 , , 平面 .
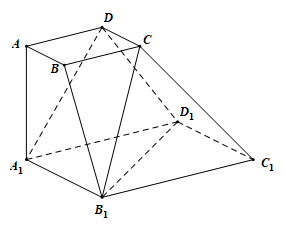 (1)、证明: 平面 ;(2)、求二面角 的平面角的大小.19. “低碳出行”,一种降低“碳”的出行,以低能耗、低污染为基础,是环保的深层次体现,在众多发达国家被广大民众接受并执行,S市即将投放一批公共自行车以方便市民出行,减少污染,缓解交通拥堵,现先对100人做了是否会考虑选择自行车出行的调查,结果如下表.(1)、如果把45周岁以下人群定义为“青年”,完成下列 列联表,并问你有多少把握认为该地区市民是否考虑单车与他(她)是不是“青年人”有关?
(1)、证明: 平面 ;(2)、求二面角 的平面角的大小.19. “低碳出行”,一种降低“碳”的出行,以低能耗、低污染为基础,是环保的深层次体现,在众多发达国家被广大民众接受并执行,S市即将投放一批公共自行车以方便市民出行,减少污染,缓解交通拥堵,现先对100人做了是否会考虑选择自行车出行的调查,结果如下表.(1)、如果把45周岁以下人群定义为“青年”,完成下列 列联表,并问你有多少把握认为该地区市民是否考虑单车与他(她)是不是“青年人”有关?年龄
考虑骑车
不考虑骑车
15以下
6
3
16
6
13
6
14
16
5
9
75以上
1
5
合计
55
45
骑车
不骑车
合计
45岁以下
45岁以上
合计
100
参考: ,
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.07
2.70
3.84
5.02
6.63
7.87
10.82
(2)、S市为了鼓励大家骑自行车上班,为此还专门在几条平时比较拥堵的城市主道建有无障碍自行车道,该市市民小明家离上班地点10km,现有两种.上班方案给他选择;方案一:选择自行车,走无障碍自行车道以19km/h的速度直达上班地点.
方案二:开车以30km/h的速度上班,但要经过A、B、C三个易堵路段,三个路段堵车的概率分别是 , , ,且是相互独立的,并且每次堵车的时间都是10分钟(假设除了堵车时间其他时间都是匀速行驶)
若仅从时间的角度考虑,请你给小明作一个选择,并说明理由.
20. 已知抛物线 与椭圆 在第一象限交于E点,且它们有公共的焦点F , O是椭圆的中心.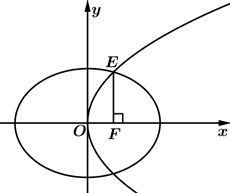
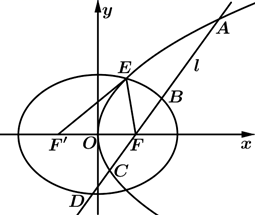 (1)、若 轴,求椭圆的离心率;(2)、若 不与 轴垂直,椭圆的另一个焦点为 ,已知 ,且 的周长为6,过F的直线l与两曲线从上至下依次交于A , B , C , D四点(其中 , , , ),若 ,求l的方程.
(1)、若 轴,求椭圆的离心率;(2)、若 不与 轴垂直,椭圆的另一个焦点为 ,已知 ,且 的周长为6,过F的直线l与两曲线从上至下依次交于A , B , C , D四点(其中 , , , ),若 ,求l的方程.