江西省南昌市2021届高三下学期理数一调考试试卷
试卷更新日期:2021-07-06 类型:高考模拟
一、单选题
-
1. 若全集 则集合 等于( )A、 B、 C、 D、2. 设 ,则 的共轭复数 ( )A、 B、 C、 D、3. “ ”是“直线 与直线 垂直”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、不充分也不必要条件4. 某地为了解居民的每日总用电量 (万度)与气温 ( )之间的关系,收集了四天的每日总用电量和气温的数据如表:
气温 ( )
19
13
9
-1
每日总用电量 (万度)
24
34
38
64
经分析,可用线性回归方程 拟合 与 的关系. 据此气温是 时,该地当日总用电量 (万度)为( )
A、32 B、31 C、29 D、285. 已知非零实数a,x,y满足 ,则下列关系式恒成立的是( )A、 B、 C、 D、6. 在直棱柱 中,若 为等边三角形,且 ,则 与 所成角的余弦值为( )A、 B、 C、 D、7. 定义在R上的函数 为偶函数, , , ,则( )A、 B、 C、 D、8. 设 的内角 , , 的对边分别为 , , ,若 , , ,则 的面积为( )A、 B、 C、4 D、9. 已知函数 的一个零点是 ,当 时函数 取最大值,则当 取最小值时,函数 在 上的最大值为( )A、-2 B、 C、 D、010. 已知 , , 是球 的球面上的三点, , , ,且球 表面积为 ,则点 到平面 的距离为( )A、2 B、 C、 D、11. 已知 为抛物线 的焦点,准线为 ,过焦点 的直线与抛物线交于 , 两点,点 在准线上的射影分别为 ,且满足 ,则 ( )A、 B、 C、3 D、12. 已知 是边长为 的正三角形, 为该三角形内切圆的一条弦,且 .若点P在 的三边上运动,则 的最大值为( )A、 B、 C、 D、二、填空题
-
13. 已知 ,则 .14. 若 的展开式中 的系数为-80,则 .15. 已知 为坐标原点,双曲线 的右焦点为 ,过点 且与 轴垂直的直线与双曲线 的一条渐近线交于点 (点 在第一象限),点 在双曲线 的渐近线上,且 ,若 ,则双曲线 的离心率为16. 已知函数 ,若方程 有两个不相等的实根,则实数a取值范围是 .
三、解答题
-
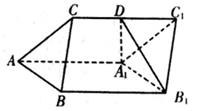
17. 在递增的等比数列 中, , , 为等差数列 的前 项和, , .(1)、求 、 的通项公式;(2)、求数列 的前 项和 .18. 如图,三棱柱 中, , ,平面 平面 .
 (1)、求证: ;(2)、若 ,直线 与平面 所成角为 , 为 的中点,求二面角 的余弦值.19. 改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
(1)、求证: ;(2)、若 ,直线 与平面 所成角为 , 为 的中点,求二面角 的余弦值.19. 改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.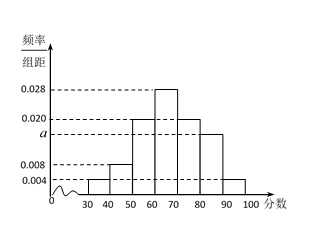
安全意识强
安全意识不强
合计
男性
女性
合计
(1)、求 的值,并估计该城市驾驶员交通安全意识强的概率;(2)、已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;(3)、在(2)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数 的分布列及期望.附: ,其中
P(K2≥k)
0.010
0.005
0.001
k
6.635
7.879
10.828
20. 在平面直角坐标系中, ,设 的内切圆分别与边 相切于点 ,已知 ,记动点 的轨迹为曲线 .(1)、求曲线 的方程;(2)、过 的直线与 轴正半轴交于点 ,与曲线E交于点 轴,过 的另一直线与曲线 交于 两点,若 ,求直线 的方程.