黑龙江省大庆市2021年中考数学试卷
试卷更新日期:2021-07-05 类型:中考真卷
一、单选题
-
1. 在 , , , 这四个数中,整数是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 北京故宫的占地面积约为720 000m2 , 将720 000用科学记数法表示为( ).A、72×104 B、7.2×105 C、7.2×106 D、0.72×1064. 下列说法正确的是( )A、 B、若 取最小值,则 C、若 ,则 D、若 ,则5. 已知 ,则分式 与 的大小关系是( )A、 B、 C、 D、不能确定6. 已知反比例函数 ,当 时,y随x的增大而减小,那么一次的数 的图像经过第( )A、一,二,三象限 B、一,二,四象限 C、一,三,四象限 D、二,三,四象限7. 一个儿何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小正方块的个数,能符合题意表示该几何体的主视图的是( )
3. 北京故宫的占地面积约为720 000m2 , 将720 000用科学记数法表示为( ).A、72×104 B、7.2×105 C、7.2×106 D、0.72×1064. 下列说法正确的是( )A、 B、若 取最小值,则 C、若 ,则 D、若 ,则5. 已知 ,则分式 与 的大小关系是( )A、 B、 C、 D、不能确定6. 已知反比例函数 ,当 时,y随x的增大而减小,那么一次的数 的图像经过第( )A、一,二,三象限 B、一,二,四象限 C、一,三,四象限 D、二,三,四象限7. 一个儿何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小正方块的个数,能符合题意表示该几何体的主视图的是( )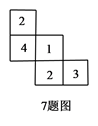 A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,F是线段 上除端点外的一点,将 绕正方形 的顶点A顺时针旋转 ,得到 .连接 交 于点H.下列结论正确的是( )
8. 如图,F是线段 上除端点外的一点,将 绕正方形 的顶点A顺时针旋转 ,得到 .连接 交 于点H.下列结论正确的是( )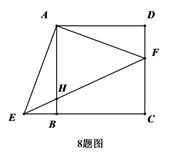 A、 B、 C、 D、9. 小刚家2019年和2020年的家庭支出如下,已知2020年的总支出2019年的总支出增加了2成,则下列说法正确的是( )
A、 B、 C、 D、9. 小刚家2019年和2020年的家庭支出如下,已知2020年的总支出2019年的总支出增加了2成,则下列说法正确的是( ) A、2020年教育方面的支出是2019年教育方面的支出的1.4倍; B、2020年衣食方面的支出比2019年衣食方面的支出增加了10%; C、2020年总支出比2019年总支出增加了2%; D、2020年其他方面的支出与2019年娱乐方面的支出相同.10. 已知函数 ,则下列说法错误的个数是( )
A、2020年教育方面的支出是2019年教育方面的支出的1.4倍; B、2020年衣食方面的支出比2019年衣食方面的支出增加了10%; C、2020年总支出比2019年总支出增加了2%; D、2020年其他方面的支出与2019年娱乐方面的支出相同.10. 已知函数 ,则下列说法错误的个数是( )①若该函数图象与 轴只有一个交点,则
②方程 至少有一个整数根
③若 ,则 的函数值都是负数
④不存在实数a,使得 对任意实数x都成立
A、0 B、1 C、2 D、3二、填空题
-
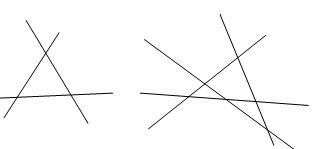
11.12. 已知 ,则13. 一个圆柱形橡皮泥,底面积是 .高是 .如果用这个橡皮泥的一半,把它捏成高为 的圆锥,则这个圆锥的底面积是14. 如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有个交点
 15. 三个数3, 在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为16. 如图,作 的任意一条直经 ,分别以 为圆心,以 的长为半径作弧,与 相交于点 和 ,顺次连接 ,得到六边形 ,则 的面积与阴影区域的面积的比值为;
15. 三个数3, 在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为16. 如图,作 的任意一条直经 ,分别以 为圆心,以 的长为半径作弧,与 相交于点 和 ,顺次连接 ,得到六边形 ,则 的面积与阴影区域的面积的比值为;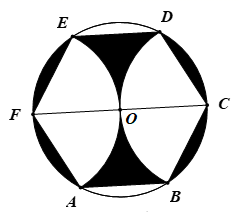 17. 某酒店客房都有三人间普通客房,双人间普通客房,收费标准为:三人间150元/间,双人间140元/间.为吸引游客,酒店实行团体入住五折优惠措施,一个46人的旅游团,优惠期间到该酒店入住,住了一些三人间普通客房和双人间普通客房,若每间客房正好住满,且一天共花去住宿费1310元,则该旅游团住了三人间普通客房和双人间普通客房共间;18. 已知,如图1,若 是 中 的内角平分线,通过证明可得 ,同理,若 是 中 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在 中, 是 的内角平分线,则 的 边上的中线长 的取值范围是
17. 某酒店客房都有三人间普通客房,双人间普通客房,收费标准为:三人间150元/间,双人间140元/间.为吸引游客,酒店实行团体入住五折优惠措施,一个46人的旅游团,优惠期间到该酒店入住,住了一些三人间普通客房和双人间普通客房,若每间客房正好住满,且一天共花去住宿费1310元,则该旅游团住了三人间普通客房和双人间普通客房共间;18. 已知,如图1,若 是 中 的内角平分线,通过证明可得 ,同理,若 是 中 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在 中, 是 的内角平分线,则 的 边上的中线长 的取值范围是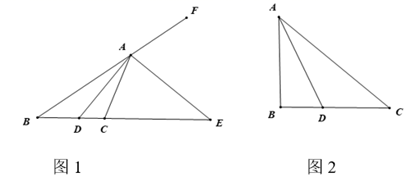
三、解答题
-
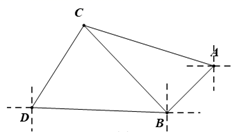
19. 计算20. 先因式分解,再计算求值: ,其中 .21. 解方程:22. 小明在A点测得C点在A点的北偏西 方向,并由A点向南偏西 方向行走到达B点测得C点在B点的北偏西 方向,继续向正西方向行走 后到达D点,测得C点在D点的北偏东 方向,求 两点之间的距离.(结果保留 ,参数数据 )
 23. 如图①是甲,乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间 之间的关系如图②所示,根据图象解答下列问题:
23. 如图①是甲,乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间 之间的关系如图②所示,根据图象解答下列问题: (1)、图②中折线 表示槽中水的深度与注入时间之间的关系;线段 表示槽中水的深度与注入时间之间的关系;铁块的高度为 .(2)、注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)24. 如图,在平行四边形 中, ,点E为线段 的三等分点(靠近点A),点F为线段 的三等分点(靠近点C,且 .将 沿 对折, 边与 边交于点G,且 .
(1)、图②中折线 表示槽中水的深度与注入时间之间的关系;线段 表示槽中水的深度与注入时间之间的关系;铁块的高度为 .(2)、注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)24. 如图,在平行四边形 中, ,点E为线段 的三等分点(靠近点A),点F为线段 的三等分点(靠近点C,且 .将 沿 对折, 边与 边交于点G,且 . (1)、证明:四边形 为矩形;(2)、求四边形 的面积.25. 某校要从甲,乙两名学生中挑选一名学生参加数学竞赛,在最近的8次选拔赛中,他们的成绩(成绩均为整数,单位:分)如下:
(1)、证明:四边形 为矩形;(2)、求四边形 的面积.25. 某校要从甲,乙两名学生中挑选一名学生参加数学竞赛,在最近的8次选拔赛中,他们的成绩(成绩均为整数,单位:分)如下:甲:92,95,96,88,92,98,99,100
乙:100,87,92,93,9▆,95,97,98
由于保存不当,学生乙有一次成绩的个位数字模糊不清,
(1)、求甲成绩的平均数和中位数;(2)、求事件“甲成绩的平均数大于乙成绩的平均数”的概率;(3)、当甲成绩的平均数与乙成绩的平均数相等时,请用方差大小说明应选哪个学生参加数学竞赛.26. 如图,一次函数 的图象与y轴的正半轴交于点A,与反比例函数 的图像交于 两点.以 为边作正方形 ,点B落在x轴的负半轴上,已知 的面积与 的面积之比为 . (1)、求一次函数 的表达式:(2)、求点P的坐标及 外接圆半径的长.27. 如图,已知 是 的直径. 是 的弦,弦 垂直 于点F,交 于点G.过点C作 的切线交 的延长线于点P
(1)、求一次函数 的表达式:(2)、求点P的坐标及 外接圆半径的长.27. 如图,已知 是 的直径. 是 的弦,弦 垂直 于点F,交 于点G.过点C作 的切线交 的延长线于点P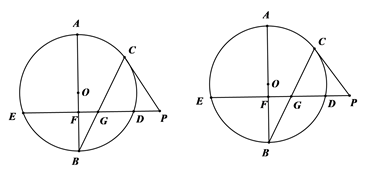 (1)、求证: ;(2)、判断 是否成立?若成立,请证明该结论;(3)、若G为 中点, , ,求 的长.28. 如图,抛物线 与 轴交于除原点 和点 ,且其顶点 关于 轴的对称点坐标为 .
(1)、求证: ;(2)、判断 是否成立?若成立,请证明该结论;(3)、若G为 中点, , ,求 的长.28. 如图,抛物线 与 轴交于除原点 和点 ,且其顶点 关于 轴的对称点坐标为 .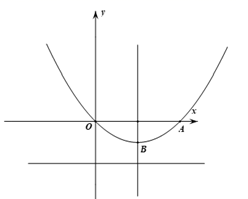 (1)、求抛物线的函数表达式;(2)、抛物线的对称轴上存在定点F,使得抛物线 上的任意一点G到定点F的距离与点G到直线 的距离总相等.
(1)、求抛物线的函数表达式;(2)、抛物线的对称轴上存在定点F,使得抛物线 上的任意一点G到定点F的距离与点G到直线 的距离总相等.①证明上述结论并求出点F的坐标;
②过点F的直线l与抛物线 交于 两点.证明:当直线l绕点F旋转时, 是定值,并求出该定值;
(3)、点 是该抛物线上的一点,在x轴,y轴上分别找点 ,使四边形 周长最小,直接写出 的坐标.