黑龙江省牡丹江市2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-07-05 类型:期中考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 满足下列条件的 不是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列命题为假命题的是( )A、对顶角相等 B、两直线平行,同位角相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、 的算术平方根是35. 如图,在平行四边形 中, 和 的平分线交 于点 , , ,则 的长为( )
 A、10 B、8 C、6 D、56. 在由边长为1的小正方形构成网格中的位置如图所示,则 边上的高是( )
A、10 B、8 C、6 D、56. 在由边长为1的小正方形构成网格中的位置如图所示,则 边上的高是( ) A、 B、 C、 D、7. 实数 在数轴上的位置如图所示,则化简 的结果为( )
A、 B、 C、 D、7. 实数 在数轴上的位置如图所示,则化简 的结果为( ) A、 B、 C、8 D、无法确定8. 在正方形 中,直线 经过对角线 , 的交点 ,过 , 两点分别作直线 的垂线,交直线 于点 , .若 , ,则 长为( )A、2 B、3 C、2或6 D、3或79. 如图,在菱形 中,点 是对角线 上一点, 是 中点,若菱形周长是16, ,则 的最小值为( )
A、 B、 C、8 D、无法确定8. 在正方形 中,直线 经过对角线 , 的交点 ,过 , 两点分别作直线 的垂线,交直线 于点 , .若 , ,则 长为( )A、2 B、3 C、2或6 D、3或79. 如图,在菱形 中,点 是对角线 上一点, 是 中点,若菱形周长是16, ,则 的最小值为( ) A、2 B、2 C、3 D、10. 如图,正方形 中, , 分别为 , 上的点, , , 交于点 , 交 于点 , 为 的中点, 交 于点 ,连接 .下列结论:① ;② ;③ ;④ ,正确的个数是( )
A、2 B、2 C、3 D、10. 如图,正方形 中, , 分别为 , 上的点, , , 交于点 , 交 于点 , 为 的中点, 交 于点 ,连接 .下列结论:① ;② ;③ ;④ ,正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 要使式子 有意义,则x的取值范围是 .12. 如图,四边形 对角线 , 交于点 . , ,请你添加一个适当的条件 , 使四边形 是菱形(只填一种情况即可).
 13. 使 是整数的最小正整数n= .
13. 使 是整数的最小正整数n= .
14. 当 时,化简 为 .15. 若 ,则代数式 的值为 .16. 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 . 17. 如图,矩形 中, ,把矩形纸片沿直线 折叠,使点 落在点 处, 交 于点 .若 .则 的长为 .
17. 如图,矩形 中, ,把矩形纸片沿直线 折叠,使点 落在点 处, 交 于点 .若 .则 的长为 . 18. 如图,矩形 的面积为12,对角线交于点 :以 , 为邻边作平行四边形 对角线交于点 ;以 , 为邻边作平行四边形 ,对角线交于点 ;…,依此类推,则平行四边形 的面积为 .
18. 如图,矩形 的面积为12,对角线交于点 :以 , 为邻边作平行四边形 对角线交于点 ;以 , 为邻边作平行四边形 ,对角线交于点 ;…,依此类推,则平行四边形 的面积为 . 19. 如图,在 中, , , 为 的中点, ,垂足为 ,若 ,则 .
19. 如图,在 中, , , 为 的中点, ,垂足为 ,若 ,则 .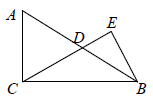 20. 等腰 中,腰 上的高 , ,则线段 的长为 .
20. 等腰 中,腰 上的高 , ,则线段 的长为 .三、解答题
-
21. 计算(1)、 ;(2)、 ;(3)、先化简再求值: ,其中 .22. 如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.
 23. 在 中, , ,以 为边作等边 ,连接 ,请画出图形,并直接写出 的面积.24. 如图,等边 的边长为 分别是 的中点,延长 至点F,使 ,连接 .
23. 在 中, , ,以 为边作等边 ,连接 ,请画出图形,并直接写出 的面积.24. 如图,等边 的边长为 分别是 的中点,延长 至点F,使 ,连接 . (1)、求证:四边形 是平行四边形;(2)、求 的长.25. 在 中,直线 经过点 , 于 , 于 , 于 .请解答下列问题:
(1)、求证:四边形 是平行四边形;(2)、求 的长.25. 在 中,直线 经过点 , 于 , 于 , 于 .请解答下列问题:

 (1)、如图①,求证: ;(提示:过点 作 于 )(2)、如图②、图③,线段 , , 之间又有怎样的数量关系?请写出你的猜想,不需要证明;(3)、在(1)(2)的条件下,若 , , ,则 .26. 在平面直角坐标系中的位置如图所示,点 在 轴正半轴上, , , 的长满足 .过点 的直线交 于点 , 的面积等于 面积的 ,请解答下列问题:
(1)、如图①,求证: ;(提示:过点 作 于 )(2)、如图②、图③,线段 , , 之间又有怎样的数量关系?请写出你的猜想,不需要证明;(3)、在(1)(2)的条件下,若 , , ,则 .26. 在平面直角坐标系中的位置如图所示,点 在 轴正半轴上, , , 的长满足 .过点 的直线交 于点 , 的面积等于 面积的 ,请解答下列问题: (1)、求点 ,点 的坐标:(2)、过点 作 于 ,交 轴于点 ,求线段 的长;(3)、点 在y轴上,平面内是否存在点 ,使以 , , , 为顶点的四边形是菱形?若存在,直接写出点 坐标;若不存在,请说明理由.
(1)、求点 ,点 的坐标:(2)、过点 作 于 ,交 轴于点 ,求线段 的长;(3)、点 在y轴上,平面内是否存在点 ,使以 , , , 为顶点的四边形是菱形?若存在,直接写出点 坐标;若不存在,请说明理由.