河北省秦皇岛市海港区2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-07-05 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,点 所在的象限是A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 函数 自变量x的取值范围是( )A、x≥1且x≠3 B、x≥1 C、x≠3 D、x>1且x≠33. 下列各曲线中表示y是x的函数的是( )A、
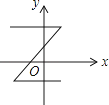 B、
B、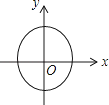 C、
C、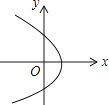 D、
D、 4. 某校八年级有 名学生,从中随机抽取了 名学生进行立定跳远测试,下列说法正确的是( )A、这种调查方式是普查 B、 名学生的立定跳远成绩是个体 C、样本容量是 D、这 名学生的立定跳远成绩是总体5. 平面直角坐标系内的点A(-1,2)与点B(-1,-2)的位置关系是( )A、关于y轴对称 B、关于x轴对称 C、关于原点对称 D、无法确定6.
4. 某校八年级有 名学生,从中随机抽取了 名学生进行立定跳远测试,下列说法正确的是( )A、这种调查方式是普查 B、 名学生的立定跳远成绩是个体 C、样本容量是 D、这 名学生的立定跳远成绩是总体5. 平面直角坐标系内的点A(-1,2)与点B(-1,-2)的位置关系是( )A、关于y轴对称 B、关于x轴对称 C、关于原点对称 D、无法确定6.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
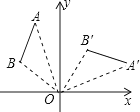 A、(2,5) B、(5,2) C、(2,﹣5) D、(5,﹣2)7. 如图,若将线段AB平移至A1B1 , 则a+b的值为( )
A、(2,5) B、(5,2) C、(2,﹣5) D、(5,﹣2)7. 如图,若将线段AB平移至A1B1 , 则a+b的值为( ) A、﹣3 B、3 C、﹣2 D、08. 如图,点 相对于点 的方向是( )
A、﹣3 B、3 C、﹣2 D、08. 如图,点 相对于点 的方向是( ) A、南偏东 B、北偏西 47° C、西偏北 47° D、东偏南 47°9. 杨老师将某次数学测试的成绩整理后绘制成如图所示的频数分布直方图,下列说法正确的是( )
A、南偏东 B、北偏西 47° C、西偏北 47° D、东偏南 47°9. 杨老师将某次数学测试的成绩整理后绘制成如图所示的频数分布直方图,下列说法正确的是( ) A、得分在60~70分的人数最多 B、人数最少的分数段的频数为4 C、得分及格(≥60分)有12人 D、该图数据分组的组距为1010. 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每天薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的( )
A、得分在60~70分的人数最多 B、人数最少的分数段的频数为4 C、得分及格(≥60分)有12人 D、该图数据分组的组距为1010. 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每天薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的( ) A、a=20 B、b=4 C、若工人甲一天获得薪金180元,则他共生产45件. D、人乙一天生产40(件),则他获得薪金140元11. 佳佳将坐标系中一图案横向拉长2倍,又向右平移2个单位长度,若想变回原来的图案,需要变化后的图案上各点坐标( )A、纵坐标不变,横坐标减2 B、纵坐标不变,横坐标先除以2,再均减2 C、纵坐标不变,横坐标除以2 D、纵坐标不变,横坐标先减2,再均除以212. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A、a=20 B、b=4 C、若工人甲一天获得薪金180元,则他共生产45件. D、人乙一天生产40(件),则他获得薪金140元11. 佳佳将坐标系中一图案横向拉长2倍,又向右平移2个单位长度,若想变回原来的图案,需要变化后的图案上各点坐标( )A、纵坐标不变,横坐标减2 B、纵坐标不变,横坐标先除以2,再均减2 C、纵坐标不变,横坐标除以2 D、纵坐标不变,横坐标先减2,再均除以212. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )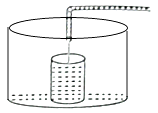 A、
A、 B、
B、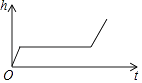 C、
C、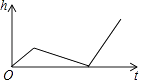 D、
D、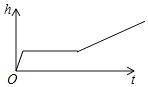
二、填空题
-
13. 点A(m+3,m+1)在x轴上,则点A坐标为 .14. 根据图中的程序,当输入x=2时,输出结果y= .
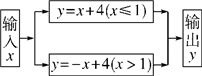 15. 已知函数 ,当 时, 是 的正比例函数.16. 已知等腰三角形的周长为4,一腰长为x,底边长为y,那么y关于x的函数关系式为 , 自变量x的取值范围是.17.
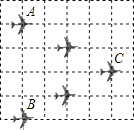
15. 已知函数 ,当 时, 是 的正比例函数.16. 已知等腰三角形的周长为4,一腰长为x,底边长为y,那么y关于x的函数关系式为 , 自变量x的取值范围是.17.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是 .
 18. 点P位于x轴下方,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是19. 如图,三角形ABC的高AD=6,BC=10,点E在边BC上运动,设BE的长为x,△ACE的面积为y,则y与x的关系式为 .
18. 点P位于x轴下方,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是19. 如图,三角形ABC的高AD=6,BC=10,点E在边BC上运动,设BE的长为x,△ACE的面积为y,则y与x的关系式为 .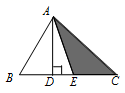 20. 如图,等边三角形ABC的顶点A、B坐标分别为(1,1)和(3,1),规定将等边三角形ABC先沿x轴翻折,再向左平移1个单位为第一次变换,则这样连续经过2021次变换后,等边三角形ABC的顶点C的坐标为 .
20. 如图,等边三角形ABC的顶点A、B坐标分别为(1,1)和(3,1),规定将等边三角形ABC先沿x轴翻折,再向左平移1个单位为第一次变换,则这样连续经过2021次变换后,等边三角形ABC的顶点C的坐标为 .
三、解答题
-
21. 随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
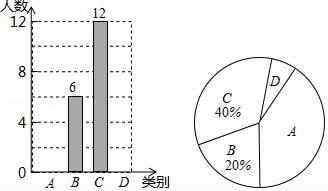
请依据统计结果回答下列问题:
(1)、本次调查中,一共调查了位好友.(2)、已知A类好友人数是D类好友人数的5倍.①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 ▲ 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
22. 如图,在平面直角坐标系 中,已知 (1)、在图中作出 ABC关于 轴的对称图形 ;(2)、若将 ABC向右平移2个单位得到 ,则点B的对应点 的坐标是;(3)、求 的长及 ABC的面积.23. 为了解某种车的耗油量,我们对这种车做了试验,并把试验的数据记录下来,制成下表:
(1)、在图中作出 ABC关于 轴的对称图形 ;(2)、若将 ABC向右平移2个单位得到 ,则点B的对应点 的坐标是;(3)、求 的长及 ABC的面积.23. 为了解某种车的耗油量,我们对这种车做了试验,并把试验的数据记录下来,制成下表:汽车行驶时间t(h)
0
1
2
3
……
剩余油量Q(L)
50
44
38
32
……
(1)、根据上表的数据,请写出Q与t的函数关系式.(2)、汽车行驶5h后,油箱中的剩余油量是多少?(3)、若汽车油箱中剩余油量为14L,则汽车行驶了多少小时?(4)、贮满50L汽油的汽车,最多行驶几小时?24. 问题情境:在平面直角坐标系 中有不重合的两点 和点 ,小明在学习中发现,若 ,则 轴,且线段 的长度为 ;若 ,则 轴,且线段 的长度为 ;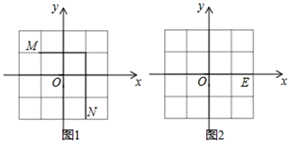 (1)、(应用)
(1)、(应用)若点 、 ,则 轴, 的长度为 .
(2)、若点 ,且 轴,且 ,则点 的坐标为 .(3)、(拓展)我们规定:平面直角坐标系中任意不重合的两点 , 之间的折线距离为 ;例如:图1中,点 与点 之间的折线距离为 .
解决下列问题:
如图1,已知 ,若 ,则 =;
(4)、如图2,已知 , ,若 ,求t的值.25. 如图,长方形ABCD中,长 cm,宽 cm,动点P在折线 上从A向C移动(点P不与点C重合),设点P运动的路径长为xcm, 的面积为 cm2 . (1)、当点P在AD上运动时, BCP的面积 , 当点P在DC上运动时, BCP的面积(填“增大”“减小”或“不变”)(2)、求y关于x的函数表达式,并指出自变量x的取值范围;(3)、当x为何值时, BCP为等腰三角形.
(1)、当点P在AD上运动时, BCP的面积 , 当点P在DC上运动时, BCP的面积(填“增大”“减小”或“不变”)(2)、求y关于x的函数表达式,并指出自变量x的取值范围;(3)、当x为何值时, BCP为等腰三角形.