北京市延庆区2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-07-05 类型:期中考试
一、单选题
-
1. 下列图象中,y是x的函数的是( )A、
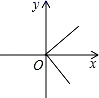 B、
B、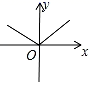 C、
C、 D、
D、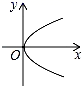 2. 在平面直角坐标系中,点P(2,﹣3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 一个六边形的内角和等于( )A、360° B、480° C、720° D、1080°4. 一次函数y=3x-2的图象不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,在 中,AE平分∠BAD,交CD边于E,AD=6,EC=4,则AB的长为( )
2. 在平面直角坐标系中,点P(2,﹣3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 一个六边形的内角和等于( )A、360° B、480° C、720° D、1080°4. 一次函数y=3x-2的图象不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,在 中,AE平分∠BAD,交CD边于E,AD=6,EC=4,则AB的长为( ) A、1 B、6 C、10 D、126. 一次函数 经过点 ,那么b的值为( )A、-4 B、4 C、8 D、-87. 下列条件中,不能判断四边形ABCD是平行四边形的是 ( )A、∠A=∠C,∠B=∠D B、AB∥CD,AB=CD C、AB=CD,AD∥BC D、AB∥CD,AD∥BC8. 如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A、1 B、6 C、10 D、126. 一次函数 经过点 ,那么b的值为( )A、-4 B、4 C、8 D、-87. 下列条件中,不能判断四边形ABCD是平行四边形的是 ( )A、∠A=∠C,∠B=∠D B、AB∥CD,AB=CD C、AB=CD,AD∥BC D、AB∥CD,AD∥BC8. 如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( ) A、线段BE B、线段EF C、线段CE D、线段DE
A、线段BE B、线段EF C、线段CE D、线段DE二、填空题
-
9. 函数 中,自变量x的取值范围是 .10. 请写出一个过点(0,1),且y随着x的增大而减小的一次函数解析式 .11. 如图,将 ABCD的一边BC延长至E,若∠A=110°,则∠1=.
 12. 在平面直角坐标系xOy中,一次函数 和 的图象如图所示,则二元一次方程组 的解为 .
12. 在平面直角坐标系xOy中,一次函数 和 的图象如图所示,则二元一次方程组 的解为 . 13. 如图,a b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5,AC=4,那么平行线a,b之间的距离为 .
13. 如图,a b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5,AC=4,那么平行线a,b之间的距离为 . 14. 若A( , ),B( , )是如图所示一次函数图象上的两个点,则 与 的大小关系是 .
14. 若A( , ),B( , )是如图所示一次函数图象上的两个点,则 与 的大小关系是 . 15. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=8,BC=6,则OD的长为 .
15. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=8,BC=6,则OD的长为 . 16. 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图所示,线段OA和折线BCDE,分别表示货车和轿车离开甲地的距离y(km)与货车离开甲地的时间x(h)之间的函数关系.
16. 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图所示,线段OA和折线BCDE,分别表示货车和轿车离开甲地的距离y(km)与货车离开甲地的时间x(h)之间的函数关系.小明根据图象,得到下列结论:
①轿车在途中停留了半小时;
②货车从甲地到乙地的平均速度是60km/h;
③轿车从甲地到乙地用的时间是4.5小时;
④轿车出发后3小时追上货车.
则小明得到的结论中正确的是(只填序号).

三、解答题
-
17. 计算: .18. 计算: .19. 已知:一次函数的图象经过点A( , )和B( , ).(1)、求这个一次函数的表达式;(2)、求这个一次函数与x轴、y轴的交点坐标.20. 解方程: .21. 已知:如图,四边形 是平行四边形, 于 , 于 .求证: .
 22. 已知:在平面直角坐标系xOy中,直线l1过点M(-3,0),且与直线l2: 相交于点B(m,4).
22. 已知:在平面直角坐标系xOy中,直线l1过点M(-3,0),且与直线l2: 相交于点B(m,4). (1)、在同一平面直角坐标系中画出直线l1和直线l2的图象;(2)、求出△BOM的面积;(3)、过动点P(n,0)且垂直于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,直接写出n的取值范围.23. 有这样一个作图题目:画一个平行四边形ABCD,使AB=3cm,BC=2cm,AC=4cm.
(1)、在同一平面直角坐标系中画出直线l1和直线l2的图象;(2)、求出△BOM的面积;(3)、过动点P(n,0)且垂直于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,直接写出n的取值范围.23. 有这样一个作图题目:画一个平行四边形ABCD,使AB=3cm,BC=2cm,AC=4cm.下面是小红同学设计的尺规作图过程.
作法:如图,
①作线段AB=3cm,
②以A为圆心,4cm为半径作弧,以B为圆心,2cm为半径作弧,两弧交于点C;
③再以C为圆心,3cm为半径作弧,以A为圆心,2cm为半径作弧,两弧交于点D;
④连结AD,BC,CD.
所以四边形ABCD即为所求作平行四边形.
根据小红设计的尺规作图过程.
 (1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下列证明.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下列证明.证明:
∵以A为圆心,4cm为半径作弧,以B为圆心,2cm为半径作弧,两弧交于点C,
∴BC= ▲ cm,AC= ▲ cm.
∵以C为圆心,3cm为半径作弧,以A为圆心,2cm为半径作弧,两弧交于点D,
∴CD=3cm.AD=2cm.
又∵AB=3cm,
∴AB=CD,AD= ▲ .
∴四边形ABCD是平行四边形( ▲ )(填推理依据).
24. 如图,在平面直角坐标系xOy中,过点A(2,0)的直线 : 与直线 : 相交于点B( ,n). (1)、求直线 的表达式;(2)、若直线 与y轴交于点C,过动点P(0,a)且平行于 的直线与线段AC有交点,求a的取值范围.25. 已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E , CE=AC .
(1)、求直线 的表达式;(2)、若直线 与y轴交于点C,过动点P(0,a)且平行于 的直线与线段AC有交点,求a的取值范围.25. 已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E , CE=AC . (1)、求证:四边形ABCD是矩形;(2)、若AB=4,AD=3,求四边形BCED的周长.26. 如图,在平面直角坐标系xOy中,我们把横纵坐标都为整数的点叫做“整点坐标”.若正比例函数 的图象与直线 及 轴围成三角形.
(1)、求证:四边形ABCD是矩形;(2)、若AB=4,AD=3,求四边形BCED的周长.26. 如图,在平面直角坐标系xOy中,我们把横纵坐标都为整数的点叫做“整点坐标”.若正比例函数 的图象与直线 及 轴围成三角形. (1)、当正比例函数 的图象过点(1,1);
(1)、当正比例函数 的图象过点(1,1);① 的值为;
②此时围成的三角形内的“整点坐标”有个;写出“整点坐标”;
(2)、若在y轴右侧,由已知围成的三角形内有3个“整点坐标”,求 的取值范围.27. 甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.(1)、以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;(2)、春节期间如何选择这两家商场去购物更省钱?28. 在平面直角坐标系xOy中,对于点 和点 ,给出如下定义:若 ,则称点 为点 的“调控变点”.例如:点(2,1)的“调控变点”为(2,1). (1)、点( ,4)的“调控变点”为;(2)、若点N(m,3)是函数 上点M的“调控变点”,求点M的坐标;(3)、点P为直线 上的动点,当 时,它的“调控变点”Q所形成的图象如图所示(端点部分为实心点).请补全当 时,点P的“调控变点” 所形成的图象.
(1)、点( ,4)的“调控变点”为;(2)、若点N(m,3)是函数 上点M的“调控变点”,求点M的坐标;(3)、点P为直线 上的动点,当 时,它的“调控变点”Q所形成的图象如图所示(端点部分为实心点).请补全当 时,点P的“调控变点” 所形成的图象.