辽宁省抚顺市顺城区2020-2021学年七年级下学期数学期中试卷

试卷更新日期：2021-07-05 类型：期中考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（）

A、4 B、±4 C、8 D、±8

查看试题解析
2. 下列各数中,无理数是（）

A、0.121221222 B、 $\frac{7}{22}$ C、 $π$ D、 $\sqrt{9}$

查看试题解析
3. 命题“垂直于同一条直线的两条直线互相平行”的条件是（）

A、垂直 B、两条直线 C、同一条直线 D、两条直线垂直于同一条直线

查看试题解析
4. 在平面直角坐标系中，把点（-4，2）先向左平移1个单位长度，再向上平移2个单位长度，得到的点的坐标是（）

A、（-5，4） B、（-5，0） C、（-3，4） D、（-3，0）

查看试题解析
5. 对于二元一次方程2x-y=7来说，当x=2时，y的值是（）

A、3 B、11 C、-3 D、-11

查看试题解析
6. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元购买A，B两种奖品（两种都要买），A种每个15元，B种每个25元，在钱全部用完的情况下，购买方案共有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
7. 已知方程组 ${\begin{array}{l} 2 x + 3 y = 14 \\ x + 4 y = 12 \end{array}$ ，则 $x - y$ 的值是（）

A、1 B、2 C、4 D、5

查看试题解析
8. 经过点A（4，2），B（6，2）作直线AB，则直线AB（）

A、过点（4，0） B、平行于x轴 C、经过原点 D、平行于y轴

查看试题解析
9. 如图，A、B的坐标分别为（﹣2，1）、（0，﹣2）．若将线段AB平移至A₁B₁ ， A₁、B₁的坐标分别为（a ， 4）、（3，b），则a+b的值为（　　）

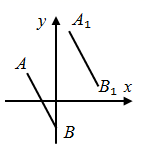A、2 B、3 C、4 D、5

查看试题解析
10. 如图，已知直线 $A B$ 、 $C D$ 被直线 $A C$ 所截， $A B / / C D$ ，E是直线 $A C$ 右边任意一点（点E不在直线 $A B$ ， $C D$ 上），设 $∠ B A E = α$ ， $∠ D C E = β$ ．下列各式：① $α + β$ ，② $α - β$ ，③ $β - α$ ，④ $360 ° - α - β$ ， $∠ A E C$ 的度数可能是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

11. $\sqrt{9}$ + $\sqrt[3]{8}$ ＝.

查看试题解析
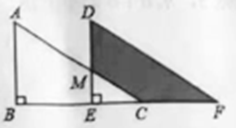
12. 若一个正数x的两个平方根分别是3m+1与﹣2m﹣3，则x的值是.

查看试题解析
13. 方程组 ${\begin{array}{l} 3 x + 2 y = 7 \\ 2 x + 3 y = 3 \end{array}$ 的解是．

查看试题解析
14. 如图，将直角三角形ABC沿 BC方向平移得直角三角形DEF，其中AB=BE=6，DM=4，则阴影部分的面积是．

查看试题解析
15. 如图，由七个完全一样的小长方形组成的大长方形 ABCD，CD=14，长方形ABCD的周长为．

查看试题解析
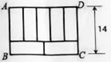16. 在同一平面内，若∠A与∠B的两边分别平行，且∠A比∠B的3 倍少40°，则∠A的度数为．

查看试题解析
17. 如图a是长方形纸带，将纸带沿 EF折叠成图b，再沿BF折叠成图c，若∠AEF=160°，则图 c 中的∠CFE的度数是度．

查看试题解析
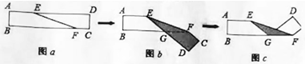18. 如图，长方形 BCDE 的各边分别平行于x轴或y轴，物体甲由点A（2，0）出发按逆时针方向以1个单位/秒的速度沿长方形 BCDE的边作环绕运动，同时物体乙由点 F（-2，0）出发按顺时针方向以2个单位/秒的速度沿长方形BCDE的边作环绕运动，则甲乙两个物体运动后的第 2021次相遇地点的坐标是．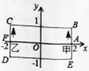

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{4} + \sqrt[3]{- 8} - \sqrt{\frac{1}{4}}$ ；

(2)、计算： $\sqrt[3]{{(- 1)}^{3}} + \sqrt[3]{27} + \sqrt{{(- 2)}^{2}} - | 1 - \sqrt{3} |$ ；

(3)、已知3a+b-1的立方根是3，2a+1的算术平方根是5，求a+b的平方根．

查看试题解析
20. 在平面直角坐标系中，三角形ABC经过平移得到三角形A′B′C′，位置如图所示．

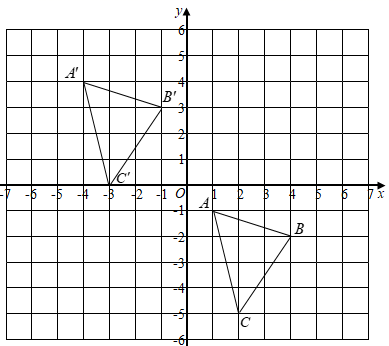(1)、点A 的坐标是， A′的坐标是．

(2)、若点M（m，n）是ABC内部一点，则平移后对应点 M的坐标为．

(3)、求△ABC的面积．

查看试题解析
21. 解方程组：

(1)、 ${\begin{array}{l} 3 x + 2 y = 19 \\ 2 x - y = 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 7 x + 2 y = 11 \\ 5 x + 4 y = 13 \end{array}$ ．

查看试题解析
22. 已知方程组 ${\begin{cases} \end{cases} \begin{matrix} 4 x - y = 5 \\ a x + b y = - 1 \end{matrix}$ 和方程组 ${\begin{cases} \end{cases} \begin{matrix} 3 x + y = 9 \\ 3 a x + 4 b y = 18 \end{matrix}$ 有相同的解，求a、b的值

查看试题解析
23. 如图，FG⊥AB，CD⊥AB，垂足分别为G、D，∠1=∠2．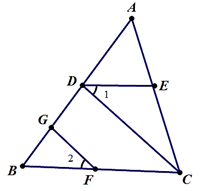

求证：DE //BC．

证明： $∵$ FG⊥AB，CD⊥AB，垂足分别为G、D（）

∴∠FGB=∠CDB=90°（    ）

∴GF//CD（    ）

∴∠2=∠BCD（    ）

又 $∵$ ∠1=∠2（已知）

∴∠1=∠BCD（    ）

∴DE //BC（    ）

查看试题解析
24. 平面直角坐标系中，O为原点，点A（0，2），B（-1，0），C（2，0）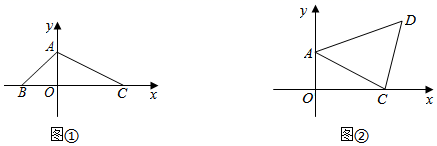

(1)、如图①，三角形 ABC的面积为；

(2)、如图②，将点B向右平移4个单位长度，再向上平移3个单位长度，得到对应点D．
① 求三角形ACD的面积；

② 点P（m，2）是一动点，若三角形PAC的面积等于三角形ACD的面积，请直接写出点P坐标．

查看试题解析
25. 如图，已知AM//BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线 AM于点 C，D．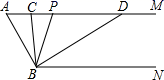

(1)、∠ABN的度数是；

(2)、求∠CBD的度数；

(3)、当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化，请写出它们之间的关系，并说明理由．若变化，请写出变化规律；

(4)、当点P运动到使∠ACB=∠ABD时，直接写出∠ABC的度数．

查看试题解析
26. 如图，直线 AB与CD交于点F，锐角∠CDE=α，∠AFC+α=180°

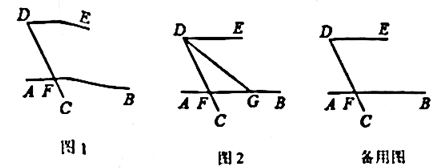(1)、如图1，求证： AB// DE；

(2)、如图2，α=70°，G为FB上一点，∠FDG与∠DGB的角平分线所在的直线交于点P．请补全图形并求∠DPG 的度数；

(3)、若G为直线AB上一点，G不与点F重合，∠FDG与∠DGB的角平分线所在的直线交于点 P．直接写出∠DPG的度数（结果用含α的式子表示）．

查看试题解析