广西贺州市2021年中考数学试卷
试卷更新日期:2021-07-05 类型:中考真卷
一、单选题
-
1. 2的倒数是( )A、 B、-2 C、 D、22. 如图,下列两个角是同旁内角的是( )
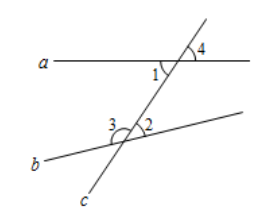 A、 与 B、 与 C、 与 D、 与3. 下列事件中属于必然事件的是( )A、任意画一个三角形,其内角和是180° B、打开电视机,正在播放新闻联播 C、随机买一张电影票,座位号是奇数号 D、掷一枚质地均匀的硬币,正面朝上4. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、(-3,2) B、(3,-2) C、(-2,-3) D、(-3,-2)5. 下列四个几何体中,左视图为圆的是( )A、
A、 与 B、 与 C、 与 D、 与3. 下列事件中属于必然事件的是( )A、任意画一个三角形,其内角和是180° B、打开电视机,正在播放新闻联播 C、随机买一张电影票,座位号是奇数号 D、掷一枚质地均匀的硬币,正面朝上4. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、(-3,2) B、(3,-2) C、(-2,-3) D、(-3,-2)5. 下列四个几何体中,左视图为圆的是( )A、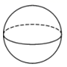 B、
B、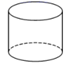 C、
C、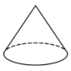 D、
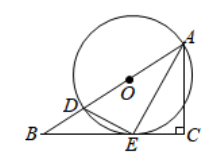
D、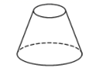 6. 直线 ( )过点 , ,则关于 的方程 的解为( )A、 B、 C、 D、7. 多项式 因式分解为( )A、 B、 C、 D、8. 若关于 的分式方程 有增根,则 的值为( )A、2 B、3 C、4 D、59. 如图,在边长为2的等边 中, 是 边上的中点,以点 为圆心, 为半径作圆与 , 分别交于 , 两点,则图中阴影部分的面积为( )
6. 直线 ( )过点 , ,则关于 的方程 的解为( )A、 B、 C、 D、7. 多项式 因式分解为( )A、 B、 C、 D、8. 若关于 的分式方程 有增根,则 的值为( )A、2 B、3 C、4 D、59. 如图,在边长为2的等边 中, 是 边上的中点,以点 为圆心, 为半径作圆与 , 分别交于 , 两点,则图中阴影部分的面积为( )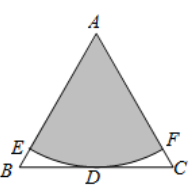 A、 B、 C、 D、10. 如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为( )
A、 B、 C、 D、10. 如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为( )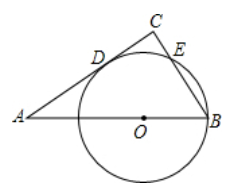 A、 B、 C、 D、111. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )
A、 B、 C、 D、111. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )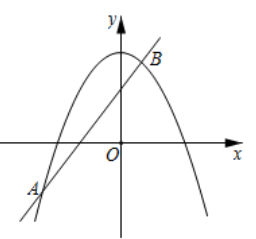 A、 或 B、 或 C、 D、12. 如 ,我们叫集合 ,其中1,2, 叫做集合 的元素.集合中的元素具有确定性(如 必然存在),互异性(如 , ),无序性(即改变元素的顺序,集合不变).若集合 ,我们说 .已知集合 ,集合 ,若 ,则 的值是( )A、-1 B、0 C、1 D、2
A、 或 B、 或 C、 D、12. 如 ,我们叫集合 ,其中1,2, 叫做集合 的元素.集合中的元素具有确定性(如 必然存在),互异性(如 , ),无序性(即改变元素的顺序,集合不变).若集合 ,我们说 .已知集合 ,集合 ,若 ,则 的值是( )A、-1 B、0 C、1 D、2二、填空题
-
13. 要使二次根式 在实数范围内有意义, 的取值范围是.14. 数据0.000000407用科学记数法表示为.15. 盒子里有4张形状、大小、质地完全相同的卡片,上面分别标着数字2,3,4,5,从中随机抽出1张后不放回,再随机抽出1张,则两次抽出的卡片上的数字之和为偶数的概率是.16. 如图,在矩形 中, , 分别为 , 的中点,以 为斜边作 , ,连接 , .若 ,则 .
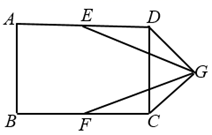 17. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.
17. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.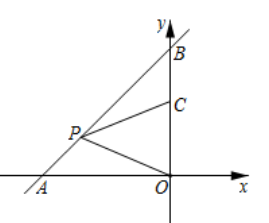 18. 如图.在边长为6的正方形 中,点 , 分别在 , 上, 且 , ,垂足为 , 是对角线 的中点,连接 、则 的长为.
18. 如图.在边长为6的正方形 中,点 , 分别在 , 上, 且 , ,垂足为 , 是对角线 的中点,连接 、则 的长为.
三、解答题
-
19. 计算: .20. 解不等式组: .21. 如图,某大学农学院的学生为了解试验田杂交水稻秧苗的长势,从中随机抽取样本对苗高进行了测量,根据统计结果(数据四舍五入取整),绘制统计图.
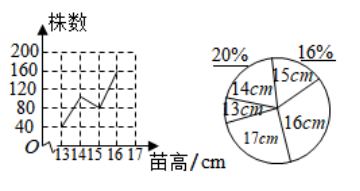 (1)、本次抽取的样本水稻秧苗为株;(2)、求出样本中苗高为 的秧苗的株数,并完成折线统计图;(3)、根据统计数据,若苗高大于或等于 视为优良秧苗,请你估算该试验田90000株水稻秧苗中达到优良等级的株数.22. 如图,一艘轮船离开 港沿着东北方向直线航行 海里到达 处,然后改变航向,向正东方向航行20海里到达 处,求 的距离.
(1)、本次抽取的样本水稻秧苗为株;(2)、求出样本中苗高为 的秧苗的株数,并完成折线统计图;(3)、根据统计数据,若苗高大于或等于 视为优良秧苗,请你估算该试验田90000株水稻秧苗中达到优良等级的株数.22. 如图,一艘轮船离开 港沿着东北方向直线航行 海里到达 处,然后改变航向,向正东方向航行20海里到达 处,求 的距离.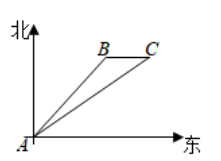 23. 为了提倡节约用水,某市制定了两种收费方式:当每户每月用水量不超过 时,按一级单价收费;当每户每月用水量超过 时,超过部分按二级单价收费.已知李阿姨家五月份用水量为 ,缴纳水费32元.七月份因孩子放假在家,用水量为 ,缴纳水费51.4元.(1)、问该市一级水费,二级大费的单价分别是多少?(2)、某户某月缴纳水费为64.4元时,用水量为多少?24. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 .
23. 为了提倡节约用水,某市制定了两种收费方式:当每户每月用水量不超过 时,按一级单价收费;当每户每月用水量超过 时,超过部分按二级单价收费.已知李阿姨家五月份用水量为 ,缴纳水费32元.七月份因孩子放假在家,用水量为 ,缴纳水费51.4元.(1)、问该市一级水费,二级大费的单价分别是多少?(2)、某户某月缴纳水费为64.4元时,用水量为多少?24. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 . (1)、求证:四边形 是菱形;(2)、若 ,求 的面积.
(1)、求证:四边形 是菱形;(2)、若 ,求 的面积.