福建省2021年中考数学试卷
试卷更新日期:2021-07-05 类型:中考真卷
一、单选题
-
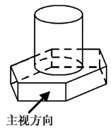
1. 在实数 , ,0,-1中,最小的数是( )A、-1 B、0 C、 D、2. 如图所示的六角螺栓,其俯视图是( )
 A、
A、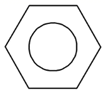 B、
B、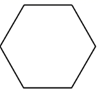 C、
C、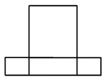 D、
D、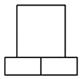 3. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
3. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )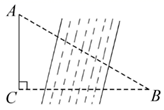 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 某校为推荐一项作品参加“科技创新”比赛,对甲、乙、丙、丁四项候选作品进行量化评分,具体成绩(百分制)如表:
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 某校为推荐一项作品参加“科技创新”比赛,对甲、乙、丙、丁四项候选作品进行量化评分,具体成绩(百分制)如表:项目
作品
甲
乙
丙
丁
创新性
90
95
90
90
实用性
90
90
95
85
如果按照创新性占60%,实用性占40%计算总成绩,并根据总成绩择优推荐,那么应推荐的作品是( )
A、甲 B、乙 C、丙 D、丁6. 某市2018年底森林覆盖率为63%.为贯彻落实“绿水青山就是金山银山”的发展理念,该市大力开展植树造林活动,2020年底森林覆盖率达到68%,如果这两年森林覆盖率的年平均增长率为x,那么,符合题意的方程是( )A、 B、 C、 D、7. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )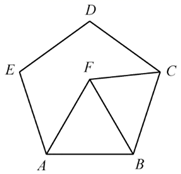 A、 B、 C、 D、8. 如图,一次函数 的图象过点 ,则不等式 的解集是( )
A、 B、 C、 D、8. 如图,一次函数 的图象过点 ,则不等式 的解集是( ) A、 B、 C、 D、9. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
A、 B、 C、 D、9. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )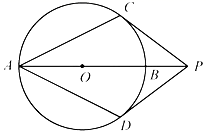 A、 B、 C、 D、10. 二次函数 的图象过 四个点,下列说法一定正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则
A、 B、 C、 D、10. 二次函数 的图象过 四个点,下列说法一定正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则二、填空题
-
11. 若反比例函数 的图象过点 ,则k的值等于.12. 写出一个无理数x,使得 ,则x可以是(只要写出一个满足条件的x即可)13. 某校共有1000名学生.为了解学生的中长跑成绩分布情况,随机抽取100名学生的中长跑成绩,画出条形统计图,如图.根据所学的统计知识可估计该校中长跑成绩优秀的学生人数是.
 14. 如图, 是 的角平分线.若 ,则点D到 的距离是.
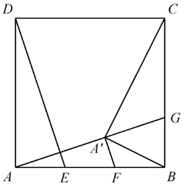
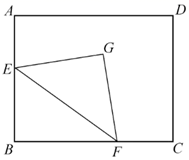
14. 如图, 是 的角平分线.若 ,则点D到 的距离是. 15. 已知非零实数x,y满足 ,则 的值等于.16. 如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:
15. 已知非零实数x,y满足 ,则 的值等于.16. 如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:① 与 一定互补;
②点G到边 的距离一定相等;
③点G到边 的距离可能相等;
④点G到边 的距离的最大值为 .
其中正确的是.(写出所有正确结论的序号)
三、解答题
-
17. 计算: .18. 如图,在 中,D是边 上的点, ,垂足分别为E,F,且 .求证: .
 19. 解不等式组:20. 某公司经营某种农产品,零售一箱该农产品的利润是70元,批发一箱该农产品的利润是40元.(1)、已知该公司某月卖出100箱这种农产品共获利润4600元,问:该公司当月零售、批发这种农产品的箱数分别是多少?(2)、经营性质规定,该公司零售的数量不能多于总数量的30%.现该公司要经营1000箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少?21. 如图,在 中, .线段 是由线段 平移得到的,点F在边 上, 是以 为斜边的等腰直角三角形,且点D恰好在 的延长线上.
19. 解不等式组:20. 某公司经营某种农产品,零售一箱该农产品的利润是70元,批发一箱该农产品的利润是40元.(1)、已知该公司某月卖出100箱这种农产品共获利润4600元,问:该公司当月零售、批发这种农产品的箱数分别是多少?(2)、经营性质规定,该公司零售的数量不能多于总数量的30%.现该公司要经营1000箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少?21. 如图,在 中, .线段 是由线段 平移得到的,点F在边 上, 是以 为斜边的等腰直角三角形,且点D恰好在 的延长线上.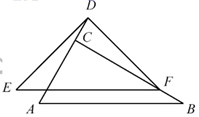 (1)、求证: ;(2)、求证: .22. 如图,已知线段 ,垂足为a.
(1)、求证: ;(2)、求证: .22. 如图,已知线段 ,垂足为a.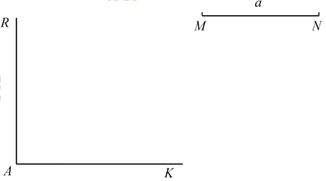 (1)、求作四边形 ,使得点B,D分别在射线 上,且 , , ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、设P,Q分别为(1)中四边形 的边 的中点,求证:直线 相交于同一点.23. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马 ,田忌也有上、中、下三匹马 ,且这六匹马在比赛中的胜负可用不等式表示如下: (注: 表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵( )获得了整场比赛的胜利,创造了以弱胜强的经典案例.
(1)、求作四边形 ,使得点B,D分别在射线 上,且 , , ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、设P,Q分别为(1)中四边形 的边 的中点,求证:直线 相交于同一点.23. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马 ,田忌也有上、中、下三匹马 ,且这六匹马在比赛中的胜负可用不等式表示如下: (注: 表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵( )获得了整场比赛的胜利,创造了以弱胜强的经典案例.假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
(1)、如果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求其获胜的概率;(2)、如果田忌事先无法打探到齐王各局的“出马”情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.