广西柳州市2021届高三理数第一次模拟考试试卷
试卷更新日期:2021-07-05 类型:高考模拟
一、单选题
-
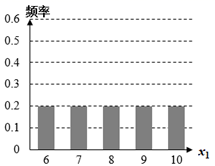
1. 已知复数 满足 (其中 为虚数单位),则 ( )A、5 B、1 C、 D、2. 设集合 , ,若 ,则实数 ( )A、2 B、1 C、-1 D、-23. 已知 、 满足约束条件 ,则 的最小值为( )A、2 B、4 C、6 D、104. 《周髀算经》是我国古老的天文学和数学著作,其书中记载:一年有二十四个节气,每个节气晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测影子的长度),夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气,其晷长依次成等差数列,经记录测算,这九个节气的所有晷长之和为49.5尺,夏至、大暑、处暑三个节气晷长之和为10.5尺,则立秋的晷长为( )A、1.5尺 B、2.5尺 C、3.5尺 D、4.5尺5. 下图为四组样本数据的条形图,则对应样本的标准差最大的是( )A、
 B、
B、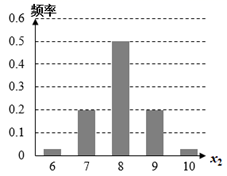 C、
C、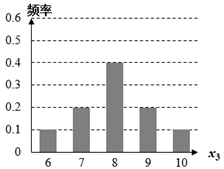 D、
D、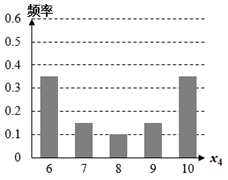 6. 已知 ,则 ( )A、 B、 C、 D、7. 函数f(x)= 在[—π,π]的图像大致为( )A、
6. 已知 ,则 ( )A、 B、 C、 D、7. 函数f(x)= 在[—π,π]的图像大致为( )A、 B、
B、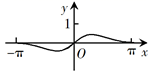 C、
C、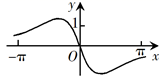 D、
D、 8. 如图所示的程序框图,当其运行结果为31时,则图中判断框①处应填入的是( )
8. 如图所示的程序框图,当其运行结果为31时,则图中判断框①处应填入的是( ) A、 B、 C、 D、9. 某几何体的三视图如图所示,则该几何体外接球的表面积是( )
A、 B、 C、 D、9. 某几何体的三视图如图所示,则该几何体外接球的表面积是( ) A、 B、 C、 D、10. 函数 的最小正周期为 ,若其图象向右平移 个单位后得到函数为奇函数,则函数 的图象( )A、关于点 对称 B、在 上单调递增 C、关于直线 对称 D、在 处取最大值11. 已知函数 的定义域为 ,且 是偶函数, 是奇函数, 在 上单调递增,则( )A、 B、 C、 D、12. 已知函数 的导函数为 ,且对任意的实数 都有 ( 是自然对数的底数),且 ,若关于 的不等式 的解集中恰有两个整数,则实数 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 函数 的最小正周期为 ,若其图象向右平移 个单位后得到函数为奇函数,则函数 的图象( )A、关于点 对称 B、在 上单调递增 C、关于直线 对称 D、在 处取最大值11. 已知函数 的定义域为 ,且 是偶函数, 是奇函数, 在 上单调递增,则( )A、 B、 C、 D、12. 已知函数 的导函数为 ,且对任意的实数 都有 ( 是自然对数的底数),且 ,若关于 的不等式 的解集中恰有两个整数,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , ,若向量 与 垂直,则 .14. 在递增等比数列 中, 是其前 项和,若 , ,则 .15. 在 展开式中, 的系数为.(结果用数字作答)16. 已知 是双曲线 的左、右焦点, 关于双曲线的一条渐近线的对称点为 ,且点 在抛物线 上,则双曲线的离心率为.
三、解答题
-
17. 在 中,角 , , 的对边分别为 , , ,且 .
 (1)、求角 的大小.(2)、若 , 为 外一点, , ,四边形 的面积是 ,求 的大小.18. 某试验小组得到6组某植物每日的光照时间 (单位: )和每日平均增长高度 (单位:mm)的数据,现分别用模型① 和模型② 对以上数据进行拟合,得到回归模型,并计算出模型的残差如下表:(模型①和模型②的残差分别为 和 ,残差 )
(1)、求角 的大小.(2)、若 , 为 外一点, , ,四边形 的面积是 ,求 的大小.18. 某试验小组得到6组某植物每日的光照时间 (单位: )和每日平均增长高度 (单位:mm)的数据,现分别用模型① 和模型② 对以上数据进行拟合,得到回归模型,并计算出模型的残差如下表:(模型①和模型②的残差分别为 和 ,残差 )5
6
7
8
9
10
0.4
3.5
5.2
7.0
8.6
10.7
-0.6
0.54
0.28
0.12
-0.24
-0.1
-0.63
1.71
2.10
1.63
-0.7
-5.42
(1)、根据上表的残差数据,应选择哪个模型来刻画该植物每日的光照时间与每日平均增长高度的关系较为合适,简要说明理由;(2)、为了优化模型,将(1)中选择的模型残差绝对值最大所对应的一组数据 剔除,根据剩余的5组数据,求该模型的回归方程,并预测光照时间为11h时,该植物的平均增长高度.(剔除数据前的参考数据: , , , , , , , , .)参考公式: , .
19. 如图,在以P为顶点的圆锥中,母线长为 ,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切.连接BC交圆于点D,连接PD,PC,E是PC的中点,连接OE,ED. (1)、求证:平面 平面PAC;(2)、若二面角 的大小为 ,求面PAC与面DOE所成锐二面角的余弦值.20. 已知椭圆 的离心率为 ,短轴长为2.(1)、求椭圆 的标准方程;(2)、设直线 与椭圆 交于 两点, 为坐标原点,若 ,
(1)、求证:平面 平面PAC;(2)、若二面角 的大小为 ,求面PAC与面DOE所成锐二面角的余弦值.20. 已知椭圆 的离心率为 ,短轴长为2.(1)、求椭圆 的标准方程;(2)、设直线 与椭圆 交于 两点, 为坐标原点,若 ,求证:点 在定圆上.
21. 已知函数 , .(1)、若 的最大值是0,求函数 的图象在 处的切线方程;(2)、若对于定义域内任意 , 恒成立,求 的取值范围.