广东省佛山市五校联盟2021届高三模拟5月数学考试试卷
试卷更新日期:2021-07-05 类型:高考模拟
一、单选题
-
1. 设 , ,则图中阴影部分表示的集合为( )
 A、 B、 C、 D、2. 在复数范围内方程 的解为( )A、 B、 C、 D、3. 在全球新冠肺炎疫情仍在流行的背景下,我国新冠病毒疫苗研发取得可喜进展,已有多款疫苗获批使用.目前我国正在按照“应接尽接、梯次推进、突出重点、保障安全”的原则,积极组织实施疫苗接种,稳步提高疫苗接种人群覆盖率.小王想从甲、乙、丙、丁四位好友中,随机邀请两位一起接种新冠病毒疫苗,则甲和乙中至少有一人被邀请的概率是( )A、 B、 C、 D、4. 2020年10月27日,在距离长江口南支航道0.7海里的风机塔上,东海航海保障中心上海航标处顺利完成临港海上风电场AIS(船舶自动识别系统)基站的新建工作,中国首个海上风机塔AIS基站宣告建成.已知风机的每个转子叶片的长度为20米,每两个叶片之间的夹角相同,风机塔(杆)的长度为60米,叶片随风转动,假设叶片与风机塔在同一平面内,如下图所示,则 的最小值为( )
A、 B、 C、 D、2. 在复数范围内方程 的解为( )A、 B、 C、 D、3. 在全球新冠肺炎疫情仍在流行的背景下,我国新冠病毒疫苗研发取得可喜进展,已有多款疫苗获批使用.目前我国正在按照“应接尽接、梯次推进、突出重点、保障安全”的原则,积极组织实施疫苗接种,稳步提高疫苗接种人群覆盖率.小王想从甲、乙、丙、丁四位好友中,随机邀请两位一起接种新冠病毒疫苗,则甲和乙中至少有一人被邀请的概率是( )A、 B、 C、 D、4. 2020年10月27日,在距离长江口南支航道0.7海里的风机塔上,东海航海保障中心上海航标处顺利完成临港海上风电场AIS(船舶自动识别系统)基站的新建工作,中国首个海上风机塔AIS基站宣告建成.已知风机的每个转子叶片的长度为20米,每两个叶片之间的夹角相同,风机塔(杆)的长度为60米,叶片随风转动,假设叶片与风机塔在同一平面内,如下图所示,则 的最小值为( ) A、40 B、 C、 D、805. 函数f (x)= ·sin x的图象的大致形状为( )A、
A、40 B、 C、 D、805. 函数f (x)= ·sin x的图象的大致形状为( )A、 B、
B、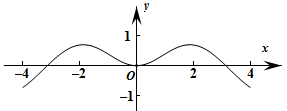 C、
C、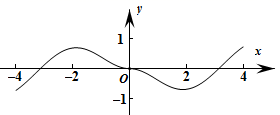 D、
D、 6. ( )A、2 B、-2 C、1 D、-17. 过双曲线 上一点 作双曲线 的切线 ,若直线 与直线 的斜率均存在,且斜率之积为 ,则双曲线 的离心率为( )A、 B、 C、 D、8. 若 ,则 的大小关系是( )A、 B、 C、 D、
6. ( )A、2 B、-2 C、1 D、-17. 过双曲线 上一点 作双曲线 的切线 ,若直线 与直线 的斜率均存在,且斜率之积为 ,则双曲线 的离心率为( )A、 B、 C、 D、8. 若 ,则 的大小关系是( )A、 B、 C、 D、二、多选题
-
9. 在“世界杯”足球赛闭幕后,某中学学生会对本校高三年级1000名学生收看比赛的情况用随机抽样方式进行调查,样本容量为50,将数据分组整理后,列表如下:
观看场数
0
1
2
3
4
5
6
7
观看人数占调查人数的百分比
8%
10%
20%
26%
m%
12%
6%
2%
从表中可以得出正确的结论为( )
A、表中m的数值为16 B、估计全年级观看比赛低于4场的学生约为32人 C、估计全年級观看比赛不低于4场的学生约为360 D、估计全年级观看比赛场数的众数为210. 函数 ,下列说法正确的是( )A、 的定义域为 B、 在定义域内单调递増 C、不等式 的解集为 D、函数 的图象关于直线 对称11. 已知圆 ,圆 ,且 不同时为0)交于不同的两点 ,下列结论正确的是( )A、 B、 C、 D、M,N为圆 上的两动点,且 ,则 的最大值为12. 已知梯形 , , , , 是线段 上的动点;将 沿着 所在的直线翻折成四面体 ,翻折的过程中下列选项中正确的是( ) A、不论何时, 与 都不可能垂直 B、存在某个位置,使得 平面 C、直线 与平面 所成角存在最大值 D、四面体 的外接球的表面积的最小值为
A、不论何时, 与 都不可能垂直 B、存在某个位置,使得 平面 C、直线 与平面 所成角存在最大值 D、四面体 的外接球的表面积的最小值为三、填空题
-
13. 已知命题 ,则该命题是(填“真命题”或“假命题”).14. 已知函数 ,则 所有的切线中斜率最小的切线方程为.15. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积= (弦 矢+ ),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为 ,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约为平方米(精确到1平方米,参考数据
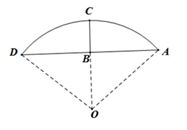 16. 古希腊数学家阿波罗尼采用平面切割圆锥的方法来研究曲线,如图①,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥与截面所成的角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线和双曲线.图②,在底面半径和高均为 的圆锥中, 、 是底面圆 的两条互相垂直的直径, 是母线 的中点, 是线段 的中点,已知过 与 的平面与圆锥侧面的交线是以E为顶点的圆锥曲线的一部分,则该曲线为 , 是该曲线上的两点且 ,若 经过点 ,则 .
16. 古希腊数学家阿波罗尼采用平面切割圆锥的方法来研究曲线,如图①,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥与截面所成的角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线和双曲线.图②,在底面半径和高均为 的圆锥中, 、 是底面圆 的两条互相垂直的直径, 是母线 的中点, 是线段 的中点,已知过 与 的平面与圆锥侧面的交线是以E为顶点的圆锥曲线的一部分,则该曲线为 , 是该曲线上的两点且 ,若 经过点 ,则 .

四、解答题
-
17. 已知数列 是等差数列,前n项和为 ;数列 是各项均为正数的等比数列,前n项和为 ;且 .(1)、分别求数列 的通项公式和前n项和 ;(2)、若将数列 中出现的数列 的项剔除后,剩余的项从小到大排列得到数列 ,记数列 的前n项和为 ,求 .18. 在 中,角A,B,C的对边分别为 ,且a<b<c,现有三个条件:①a、b、c为连续偶数;② ;③ .(1)、从上述三个条件中选出 ▲ 两个,使得 不存在,并说明理由;(2)、从上述三个条件中选出 ▲ 两个,使得 存在;若△ABC存在且唯一,请求出a的值;若 存在且不唯一,请说明理由.19. 已知如图①,在菱形 中, 且 , 为 的中点,将 沿 折起使 ,得到如图②所示的四棱锥 .
 (1)、求证:平面 平面 ;(2)、若 为 的中点,求二面角 的余弦值.20. 某科技公司组织技术人员进行某新项目研发,技术人员将独立地进行项日中不同类型的实验甲、乙、丙,已知实验甲、乙、丙成功的概率分别为 、 、 .(1)、对实验甲、乙、丙各进行一次,求至少有一次成功的概率;(2)、该项目研发流程如下:实验甲做一次,若成功,则奖励技术人员1万元并进行实验乙,否则技术人员不获得奖励且该项目终止;实验乙做两次,若两次都成功,则追加技术人员3万元奖励并进行实验丙,否则技术人员不追加奖励且该项目终止;实验丙做三次,若至少两次成功,则项目研发成功,再追加技术员4万元奖励,否则不追加奖励且该项目终止.每次实验相互独立,用X(单位:万元)表示技术人员所获得奖励的数值,写出X的分布列及数学期望.
(1)、求证:平面 平面 ;(2)、若 为 的中点,求二面角 的余弦值.20. 某科技公司组织技术人员进行某新项目研发,技术人员将独立地进行项日中不同类型的实验甲、乙、丙,已知实验甲、乙、丙成功的概率分别为 、 、 .(1)、对实验甲、乙、丙各进行一次,求至少有一次成功的概率;(2)、该项目研发流程如下:实验甲做一次,若成功,则奖励技术人员1万元并进行实验乙,否则技术人员不获得奖励且该项目终止;实验乙做两次,若两次都成功,则追加技术人员3万元奖励并进行实验丙,否则技术人员不追加奖励且该项目终止;实验丙做三次,若至少两次成功,则项目研发成功,再追加技术员4万元奖励,否则不追加奖励且该项目终止.每次实验相互独立,用X(单位:万元)表示技术人员所获得奖励的数值,写出X的分布列及数学期望.