广东省2021年普通高中数学学业水平考试试卷

试卷更新日期：2021-07-05 类型：高考模拟

进入出卷网下载

一、单选题

1. 设全集U= ${1 ， 2 ， 3 ， 4 ， 5}$ ，A= ${1 ， 2}$ ，则 $∁_{U} A =$ （）

A、 ${1 ， 2 ， 3 ， 4 ， 5}$ B、 ${2 ， 3 ， 4 ， 5}$ C、 ${3 ， 4 ， 5}$ D、 ${3 ， 4}$

查看试题解析
2. 已知 $\cos (\frac{π}{2} - α) = \frac{1}{2}$ ，则 $sin α$ = （）

A、 $\frac{1}{2}$ B、- $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 - $\frac{\sqrt{3}}{2}$

查看试题解析
3. 下列函数为偶函数的是（）

A、 $f (x) = x + 1$ B、 $f (x) = \frac{1 + x^{2}}{x^{2}}$ C、 $f (x) = x^{3}$ D、 $f (x) = \sin x$

查看试题解析
4. 已知a=0.2³ ， b=0.3² ， c=0.3³ ，则a，b，c的大小关系是（）

A、a＜c＜b B、b＜a＜c C、c＜a＜b D、a＜b＜c

查看试题解析
5. 经过点 $A (- 1 ， 6) ， B (0 ， 2)$ 的直线的方程是（）

A、 $x - 4 y - 2 = 0$ B、 $4 x - y - 2 = 0$ C、 $x + 4 y - 2 = 0$ D、 $4 x + y - 2 = 0$

查看试题解析
6. 连续抛掷两枚骰子，向上点数之和为6的概率为（）

A、 $\frac{1}{12}$ B、 $\frac{1}{11}$ C、 $\frac{5}{36}$ D、 $\frac{1}{6}$

查看试题解析
7. 下列函数在其定义域内为减函数的是（）

A、 $f (x) = x^{3}$ B、 $f (x) = \frac{1}{2} x + 1$ C、 $f (x) = \log_{3} x$ D、 $f (x) = {(\frac{1}{3})}^{x}$

查看试题解析
8. 已知直线a，b与平面 $α$ ，若a平行 $α$ ，b在 $α$ 内，则下列结论正确的是（）

A、 $a // b$ B、a与b是异面直线 C、 $\vec{a} ⊥ \vec{b}$ D、以上情况都有可能

查看试题解析
9. 不等式4-x²≤0的解集为（）

A、 ${x | - 2 \leq x \leq 2}$ B、 ${x | x \leq - 2$ 或 $x \geq 2}$ C、 ${x | - 4 \leq x \leq 4}$ D、 ${x | x \leq - 4$ 或 $x \geq 4}$

查看试题解析
10. 下列计算正确的是（）

A、5²×5^-2=0 B、 ${(\frac{2}{5})}^{\frac{5}{2}}$ = 1 C、 $\lg 2$ + $\lg 5$ = $\lg 7$ D、 $\log_{2} \sqrt[3]{8} = 1$

查看试题解析
11. 圆心在C（4，-3），且与直线4x-3y=0相切的圆的方程为（）

A、x²+y²+8x+6y=0 B、x²+y²+8x-6y=0 C、x²+y²-8x+6y=0 D、x²+y²-8x-6y=0

查看试题解析
12. 如图是表示某班6名学生期末数学考试成绩的茎叶图，则这6名学生的平均成绩为（）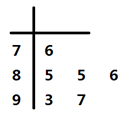

A、87 B、86 C、85.5 D、85

查看试题解析
13. 我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（）

A、1盏 B、3盏 C、5盏 D、9盏

查看试题解析
14. 为了得到 $y = \sin (x - \frac{π}{3})$ 的图象，只需把函数 $y = \sin x$ 的图象上的所有点（）

A、向右平行移动 $\frac{π}{3}$ 个单位长度 B、向左平行移动 $\frac{π}{3}$ 个单位长度 C、向右平行移动 $\frac{π}{6}$ 个单位长度 D、向左平行移动 $\frac{π}{6}$ 个单位长度

查看试题解析
15. 已知a＞0，b＞0，a+b=1， $\frac{1}{a}$ + $\frac{2}{b}$ 的最小值是（）

A、 $\frac{10}{3}$ B、6 C、 $3 + 2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析

二、填空题

16. 已知向量 $\vec{a} = (2 ， m) ， \vec{b} = (1 ， - 2)$ ，若 $\vec{a}$ 与 $\vec{b}$ 共线，则m = .

查看试题解析
17. 设 $\tan θ = 2$ ，则 $\tan (θ + \frac{π}{4}) =$ .

查看试题解析
18. 在等差数列 ${a_{n}}$ 中，已知a₃=6，a₅=a₂+9，则a₆= .

查看试题解析
19. 已知函数 $f (x) = {\begin{matrix} 2^{x} ， x \leq 0 \\ \log_{2} x ， x > 0 \end{matrix}$ ；设 $f (- 2) = a$ ，则 $f (a) =$ .

查看试题解析

三、解答题

20. 食品安全问题越来越引起人们的重视，为了给消费者提供放心的蔬菜，某农村合作社搭建了两个无公害蔬菜大棚，分别种植西红柿和黄瓜，根据以往的种植经验，发现种植西红柿的年利润P（单位：万元），种植黄瓜的年利润Q（单位：万元）与投入的资金x（4≤x≤16，单位：万元）满足P= $4 \sqrt{2 x}$ + 8，Q= $\frac{1}{4} x + 12$ .现合作社共筹集了20万元，将其中8万元投入种植西红柿，剩余资金投入种植黄瓜.求这两个大棚的年利润总和.

查看试题解析
21. 如图，在△ABC中，∠A=30°，D是边AB上的点，CD=5，CB=7，DB=3

(1)、求△CBD的面积；

(2)、求边AC的长.

查看试题解析
22. 如图，在四棱锥P-ABCD中，底边ABCD是边长为2的菱形，PA=AC=2，PA⊥平面ABC，E，F分别为PD，BC的中点.

(1)、求三棱锥P-ABD的体积；

(2)、证明：EF∥平面PAB（参考公式：锥体的体积公式为V= $\frac{1}{3} S h$ ，其中S是锥体的底面积，h是锥体的高）

查看试题解析