安徽省皖江名校2021届高三文数5月最后一卷
试卷更新日期:2021-07-05 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 已知复数z满足 ,则下列结论正确的是( )A、 B、 C、 D、3. 从2020开始智慧课堂建设逐渐在全国各地中小学中推广,智慧课堂教学系统中,对学生的个性化教育分析全面及时,某市利用智慧课堂,对某次联考的两个学校的语文、数学,历史、地理和化学五科的平均成绩进行分析比较,得到如下的雷达图,下列说法正确的是( )
 A、A校各科的成绩较为均衡,各科的平均成绩相当 B、A校和B校在地理科上的成绩差距比在数学科目上的成绩差距大 C、A校和B校的历史成绩差距较大 D、A校语文、数学、地理,历史,化学这五门课的成绩都比B校差4. 函数 的大致图象为( )A、
A、A校各科的成绩较为均衡,各科的平均成绩相当 B、A校和B校在地理科上的成绩差距比在数学科目上的成绩差距大 C、A校和B校的历史成绩差距较大 D、A校语文、数学、地理,历史,化学这五门课的成绩都比B校差4. 函数 的大致图象为( )A、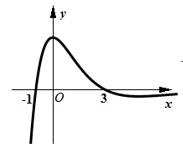 B、
B、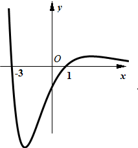 C、
C、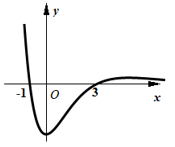 D、
D、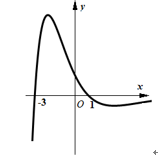 5. 《九章算术》是中国古代的数学专著,在卷五《商功》重有一问题:今有沟,上广一丈五尺,下广一丈,深五尺,袤七丈.问积几何?答曰:四千三百七十尺.意思是说现在有一条水沟,截面是梯形,梯形上底长一丈五尺,下底长一丈,水沟的深为五尺,长七丈.问水沟的容积是多大?答案是4375立方尺.若此沟两坡面坡度相同,某人想给此沟表面铺上水泥进行固定,不计水泥厚度,则需要水泥多少平方尺?(一丈等于十尺)( )A、4375 B、 C、 D、6. 偶函数 满足 ,且在 时, ,则 ( )A、 B、1 C、 D、7. 在 中, , , ,则 ( )A、 B、1 C、2 D、38. 已知 , 为锐角, , ,则 ( )A、 B、 C、 D、9. 已知 , 是双曲线 上两点,直线 垂直于双曲线的实轴,原点 到直线 的距离为 ,且 ,则双曲线的离心率为( )A、 B、 C、 或 D、 或10. 已知函数 ,且函数 的最小正周期为 ,则下列关于函数 的说法,
5. 《九章算术》是中国古代的数学专著,在卷五《商功》重有一问题:今有沟,上广一丈五尺,下广一丈,深五尺,袤七丈.问积几何?答曰:四千三百七十尺.意思是说现在有一条水沟,截面是梯形,梯形上底长一丈五尺,下底长一丈,水沟的深为五尺,长七丈.问水沟的容积是多大?答案是4375立方尺.若此沟两坡面坡度相同,某人想给此沟表面铺上水泥进行固定,不计水泥厚度,则需要水泥多少平方尺?(一丈等于十尺)( )A、4375 B、 C、 D、6. 偶函数 满足 ,且在 时, ,则 ( )A、 B、1 C、 D、7. 在 中, , , ,则 ( )A、 B、1 C、2 D、38. 已知 , 为锐角, , ,则 ( )A、 B、 C、 D、9. 已知 , 是双曲线 上两点,直线 垂直于双曲线的实轴,原点 到直线 的距离为 ,且 ,则双曲线的离心率为( )A、 B、 C、 或 D、 或10. 已知函数 ,且函数 的最小正周期为 ,则下列关于函数 的说法,① ;
②点 是 的一个对称中心;
③直线 是函数 的一条对称轴;
④函数 的单调递增区间是 .
其中正确的( )
A、①②④ B、①②③ C、②③④ D、①③④11. 已知四边形ABCD是圆内接四边形, ,则ABCD的周长取最大值时,四边形ABCD的面积为( )A、 B、 C、 D、12. 已知函数 ,方程 有两解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 抛物线 上一点 到点 的距离等于3,则 .14. 已知 ,则曲线 在点 处的切线方程为.15. 从古至今,奇门遁甲,五行八卦等,我们称之为玄学,它充满了神秘色彩,我们常说“无极生太极,太极生两仪,两仪生四象,四象生八卦”.下图是伏羲先天八卦生成图.八卦是由
 组合而成,八卦中的阳爻和阴爻这与计算机数制“二进制”中的1和0分别对应,例如在二进制下“110001”表示的“十进制”数为 ,在八卦中益卦
组合而成,八卦中的阳爻和阴爻这与计算机数制“二进制”中的1和0分别对应,例如在二进制下“110001”表示的“十进制”数为 ,在八卦中益卦  代表的二进制数为“110001”表示十进制数49,据此,恒卦
代表的二进制数为“110001”表示十进制数49,据此,恒卦  表示的十进制数字为. 16. 在三棱锥 中,底面 是以 为斜边的等腰直角三角形,且 , , 与底面 所成的角的余弦值为 ,则三棱锥 的外接球的表面积为.
表示的十进制数字为. 16. 在三棱锥 中,底面 是以 为斜边的等腰直角三角形,且 , , 与底面 所成的角的余弦值为 ,则三棱锥 的外接球的表面积为.三、解答题
-
17. 数列 中, .(1)、求数列 的通项公式;(2)、设 若数列 的前n项的和是 ,求证: .18. 已知正方形 的边长为2,点 分别是 , 的中点,沿 把 折起得到几何体 .
 (1)、当 时,求证: .(2)、当平面 平面 时,求三棱锥 的体积.19. 2020年第七次全国人口普查摸底工作从10月11日开始,10月31日结束.从11月1日开始进入普查的正式登记阶段.普查员要进入每个住户逐人逐项登记普查信息,这期间还将随机抽取10%的住户填报普查长表,调查更为详细的人口结构信息.整个登记工作持续到12月10日结束.某社区对随机抽取的10%住户普查长表信息情况汇总,发现其中30%的住户是租房入住,现对租房户按照住户家庭年人均收入情况绘制出如下的频率分布直方图(假设该社区内住户家庭年房租支出均在2到8万之间):
(1)、当 时,求证: .(2)、当平面 平面 时,求三棱锥 的体积.19. 2020年第七次全国人口普查摸底工作从10月11日开始,10月31日结束.从11月1日开始进入普查的正式登记阶段.普查员要进入每个住户逐人逐项登记普查信息,这期间还将随机抽取10%的住户填报普查长表,调查更为详细的人口结构信息.整个登记工作持续到12月10日结束.某社区对随机抽取的10%住户普查长表信息情况汇总,发现其中30%的住户是租房入住,现对租房户按照住户家庭年人均收入情况绘制出如下的频率分布直方图(假设该社区内住户家庭年房租支出均在2到8万之间): (1)、求出 的值(2)、若抽取的10%住户中,家庭人均年收入在 万元的恰好有12户,则该社区共有住户约多少户.(3)、若从家庭年房租支出不到6万元的住户中按照分层抽样的方法抽取10户,再从这10户中随机抽取2户对其住房和医疗保健情况进行调查,求抽得的2户家庭年房租支出少于5万元不少于3万元的概率.20. 已知椭圆 的离心率为 ,右顶点 ,直线 与椭圆C相交于P,Q两点(1)、求椭圆C的方程.(2)、如果 ,点M关于直线l的对称点N在y轴上,求k的值.
(1)、求出 的值(2)、若抽取的10%住户中,家庭人均年收入在 万元的恰好有12户,则该社区共有住户约多少户.(3)、若从家庭年房租支出不到6万元的住户中按照分层抽样的方法抽取10户,再从这10户中随机抽取2户对其住房和医疗保健情况进行调查,求抽得的2户家庭年房租支出少于5万元不少于3万元的概率.20. 已知椭圆 的离心率为 ,右顶点 ,直线 与椭圆C相交于P,Q两点(1)、求椭圆C的方程.(2)、如果 ,点M关于直线l的对称点N在y轴上,求k的值.