初中数学浙教版八年级上册2.8 直角三角形全等的判定 同步练习
试卷更新日期:2021-07-02 类型:同步测试
一、单选题
-
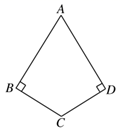
1. 如图,∠BAD=∠BCD=90°,AB=CB,据此可以证明△BAD≌△BCD,证明的依据是 ( )
 A、AAS B、ASA C、SAS D、HL2. 在 中, ,E是AB上一点,且 ,过E作 交AC于D,如果 ,则 等于( )
A、AAS B、ASA C、SAS D、HL2. 在 中, ,E是AB上一点,且 ,过E作 交AC于D,如果 ,则 等于( )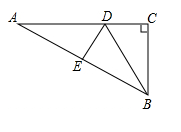 A、3cm B、4cm C、5cm D、6cm3. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A、3cm B、4cm C、5cm D、6cm3. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ) A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均错误4. 如图,∠C=∠D=90°,若添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,则以下给出的条件适合的是( )
A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均错误4. 如图,∠C=∠D=90°,若添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,则以下给出的条件适合的是( ) A、AC=AD B、AB=AB C、∠ABC=∠ABD D、∠BAC=∠BAD5. 如图,在 中, ,在 上取一点E,使 ,过点E作 ,连接 ,使 ,若 ,则下列结论错误的是( )
A、AC=AD B、AB=AB C、∠ABC=∠ABD D、∠BAC=∠BAD5. 如图,在 中, ,在 上取一点E,使 ,过点E作 ,连接 ,使 ,若 ,则下列结论错误的是( ) A、 B、 C、 平分 D、6. 如图,点P是∠AOB的平分线上的一点,作PD⊥OA,PE⊥OB,垂足分别是D、E.连接DE交OC于点F.则图中共有( )个直角
A、 B、 C、 平分 D、6. 如图,点P是∠AOB的平分线上的一点,作PD⊥OA,PE⊥OB,垂足分别是D、E.连接DE交OC于点F.则图中共有( )个直角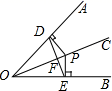 A、4 B、6 C、8 D、107. 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是 (填判定三角形全等方法的简称)( )
A、4 B、6 C、8 D、107. 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是 (填判定三角形全等方法的简称)( ) A、SSS B、SAS C、ASA D、HL8. 下列命题中,是假命题的是( )A、两条直角边对应相等的两个直角三角形全等 B、两个锐角对应相等的两个直角三角形全等 C、斜边和一条直角边对应相等的两个直角三角形全等 D、斜边和一个锐角对应相等的两个直角三角形全等9. 如图,在 中, , 于D , ,如果 ,那么 等于( )
A、SSS B、SAS C、ASA D、HL8. 下列命题中,是假命题的是( )A、两条直角边对应相等的两个直角三角形全等 B、两个锐角对应相等的两个直角三角形全等 C、斜边和一条直角边对应相等的两个直角三角形全等 D、斜边和一个锐角对应相等的两个直角三角形全等9. 如图,在 中, , 于D , ,如果 ,那么 等于( ) A、 B、3m C、 D、4m10. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
A、 B、3m C、 D、4m10. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( ) A、1对 B、2对 C、3对 D、4对11. 如图,在 中, 是AC上一点, 于点E, 连接BD,若AC=8cm,则 等于( )
A、1对 B、2对 C、3对 D、4对11. 如图,在 中, 是AC上一点, 于点E, 连接BD,若AC=8cm,则 等于( )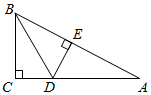 A、6cm B、7cm C、8cm D、9cm12. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A、6cm B、7cm C、8cm D、9cm12. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( ) A、AC=AD B、AC=BC C、∠ABC=∠ABD D、∠BAC=∠BAD13. 如图, 于 , 于 ,若 , 平分 ,则下列结论:① ;② ;③ ;④ ,正确的有( )个
A、AC=AD B、AC=BC C、∠ABC=∠ABD D、∠BAC=∠BAD13. 如图, 于 , 于 ,若 , 平分 ,则下列结论:① ;② ;③ ;④ ,正确的有( )个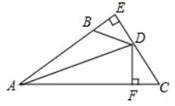 A、 B、 C、 D、14. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、 B、 C、 D、14. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )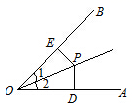 A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OP15. 如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OP15. 如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )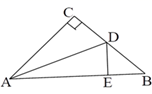 A、4cm B、8cm C、10cm D、14cm
A、4cm B、8cm C、10cm D、14cm二、填空题
-
16. 如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD , 你添加的条件是 .
 17. 如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB= .
17. 如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB= . 18. 如图,在 中, , , ,射线 于点A,点E、D分别在线段 和射线 上运动,并始终保持 ,要使 和 全等,则 的长为.
18. 如图,在 中, , , ,射线 于点A,点E、D分别在线段 和射线 上运动,并始终保持 ,要使 和 全等,则 的长为.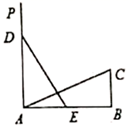 19. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是
19. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 20. 如图, , , 于点 , 于点 , , ,则 的长是 .
20. 如图, , , 于点 , 于点 , , ,则 的长是 .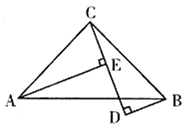 21. 如图,在∠AOB的两边上,分别取OM = ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则△OPM≌△OPN,从而得到OP平分∠AOB,其判定三角形全等的依据是.
21. 如图,在∠AOB的两边上,分别取OM = ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则△OPM≌△OPN,从而得到OP平分∠AOB,其判定三角形全等的依据是. 22. 如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是(填一个即可).
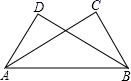
22. 如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是(填一个即可).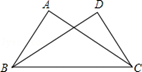 23. 如图,已知AB⊥BD , AB∥ED , AB=ED , 要证明ΔABC≌ΔEDC , 若以“SAS”为依据,还要添加的条件为;若添加条件AC=EC , 则可以用方法判定全等.
23. 如图,已知AB⊥BD , AB∥ED , AB=ED , 要证明ΔABC≌ΔEDC , 若以“SAS”为依据,还要添加的条件为;若添加条件AC=EC , 则可以用方法判定全等.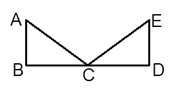 24. 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E,D,BD=CF,BE=CD.若∠AFD=155°,则∠EDF= .
24. 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E,D,BD=CF,BE=CD.若∠AFD=155°,则∠EDF= . 25. 已知:如图, 中,AB=AC,AD是高,则≌ .依据是 , 并且BD= , ∠BAD= .
25. 已知:如图, 中,AB=AC,AD是高,则≌ .依据是 , 并且BD= , ∠BAD= .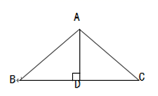
三、计算题
-
26. 如图,AC⊥BD , 垂足点E是BD的中点,且AB=CD , 求证:AB//CD.

四、解答题