初中数学浙教版八年级上册2.7 探索勾股定理 同步练习
试卷更新日期:2021-07-02 类型:同步测试
一、单选题
-
1. 以下列各组数为三边的三角形中不是直角三角形的是( )A、3, 4,5 B、 13,5,12 C、5,6,7 D、41,40,92. 如图, 、 、 、 是四根长度均为5cm的火柴棒,点A、C、E共线.若 , ,则线段 的长度为( )
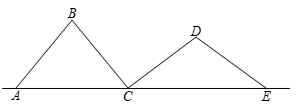 A、6 cm B、7 cm C、 D、8cm3. 已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=( )
A、6 cm B、7 cm C、 D、8cm3. 已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=( )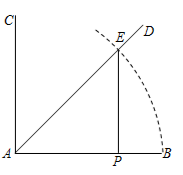 A、 B、 C、 D、4.
A、 B、 C、 D、4.钓鱼岛和中国台湾属于同一地质构造,按照国际法钓鱼岛属于中国.钓鱼岛周围海域石油资源丰富,地域战略十分重要.图中A为台湾基隆,B为钓鱼岛,单位长度为38千米,那么A,B相距( )
 A、190千米 B、266千米 C、101千米 D、950千米5. 如图,一次函数 的图像与x轴、y轴分别交于点A、B,把直线 绕点B顺时针旋转 交x轴于点C,则线段 长为( )
A、190千米 B、266千米 C、101千米 D、950千米5. 如图,一次函数 的图像与x轴、y轴分别交于点A、B,把直线 绕点B顺时针旋转 交x轴于点C,则线段 长为( ) A、 B、 C、 D、6. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是 ( )
A、 B、 C、 D、6. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是 ( ) A、2 B、8 C、2 D、107. 如图,在3×4的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )
A、2 B、8 C、2 D、107. 如图,在3×4的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )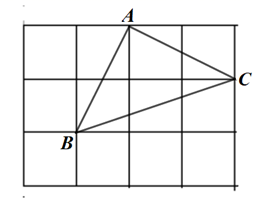 A、是直角三角形 B、 C、面积为4 D、 边上的高为8. 如图,数轴上点C所表示的数是( )
A、是直角三角形 B、 C、面积为4 D、 边上的高为8. 如图,数轴上点C所表示的数是( ) A、 B、 C、3.6 D、3.79. 如图是小军设计的一面彩旗,其中 , ,点 在 上, ,则 的长为( )
A、 B、 C、3.6 D、3.79. 如图是小军设计的一面彩旗,其中 , ,点 在 上, ,则 的长为( ) A、 B、 C、 D、10. 如图,在 的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )
A、 B、 C、 D、10. 如图,在 的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )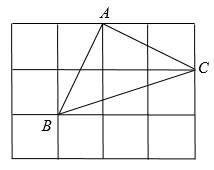 A、是直角三角形 B、tam C、面积为 D、 边上的高为11. 如图所示,在正方形 中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为 的正方形,则下列等式成立的是( )
A、是直角三角形 B、tam C、面积为 D、 边上的高为11. 如图所示,在正方形 中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为 的正方形,则下列等式成立的是( ) A、 B、 C、 D、12. 如图,AB为某河流的宽,为了估测河流的宽,在笔直的河岸上依此取点C,E,B,F,使DE⊥CF,且DA∥CF,测得CE=2米,EB=4米,BF=7米,且∠C=∠FDC,则AB的长为( )米
A、 B、 C、 D、12. 如图,AB为某河流的宽,为了估测河流的宽,在笔直的河岸上依此取点C,E,B,F,使DE⊥CF,且DA∥CF,测得CE=2米,EB=4米,BF=7米,且∠C=∠FDC,则AB的长为( )米 A、 B、6.9 C、 D、713. 如图,在正方形方格纸中,每个小正方形的边长都是1,点 , , , 都在格点处, 与 相交于点 ,则 的值是( )
A、 B、6.9 C、 D、713. 如图,在正方形方格纸中,每个小正方形的边长都是1,点 , , , 都在格点处, 与 相交于点 ,则 的值是( ) A、 B、 C、 D、14. 已知△ABC中,AB=13,AC=15,AD⊥BC于D , 且AD=12,则BC的长为( )A、14 B、4 C、14或4 D、14或915. 已知a、b为两正数,且 ,则代数式 最小值为( )A、12 B、13 C、14 D、15
A、 B、 C、 D、14. 已知△ABC中,AB=13,AC=15,AD⊥BC于D , 且AD=12,则BC的长为( )A、14 B、4 C、14或4 D、14或915. 已知a、b为两正数,且 ,则代数式 最小值为( )A、12 B、13 C、14 D、15二、填空题
-
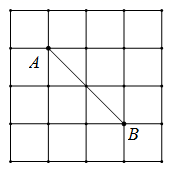
16. 如图,点 、点 均在边长为 的正方形网格的格点上,则线段 的长度3.(填“>”, “=”或“<”)
 17. 如图, 中, , , 平分 交 于点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 和点 ,作直线 ,交 于点 ,则 的长为.
17. 如图, 中, , , 平分 交 于点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 和点 ,作直线 ,交 于点 ,则 的长为. 18. 如图,在扇形 中, ,点 是 的中点,点 , 分别为半径 , 上的动点.若 ,则 周长的最小值为.
18. 如图,在扇形 中, ,点 是 的中点,点 , 分别为半径 , 上的动点.若 ,则 周长的最小值为. 19. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸.
19. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸.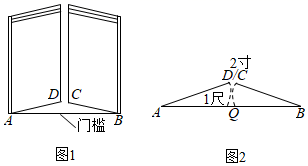 20. 如图所示的正方形网格内,点A , B , C , D , E是网格线交点,那么 °.
20. 如图所示的正方形网格内,点A , B , C , D , E是网格线交点,那么 °.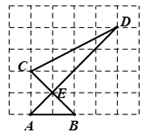 21. 如图所示的网格是正方形网格,A , B , C , D是网格线交点,则 与 的大小关系为: (填“>”,“=”或“<”).
21. 如图所示的网格是正方形网格,A , B , C , D是网格线交点,则 与 的大小关系为: (填“>”,“=”或“<”). 22. 如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建梯子,并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是12米,则梯子最短长度为 .
22. 如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建梯子,并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是12米,则梯子最短长度为 . 23. 如图,在△ABC中,∠BAC=90°,AB:AC=3:4,点D是BC上一点,AB=BD , 连接AD , 作BE⊥AD于点E , 连接CE , 若AD=12,则△ACE的面积为 .
23. 如图,在△ABC中,∠BAC=90°,AB:AC=3:4,点D是BC上一点,AB=BD , 连接AD , 作BE⊥AD于点E , 连接CE , 若AD=12,则△ACE的面积为 . 24. 如图所示,在正方形网格中,点A , B , C , D为网格线的交点,线段 与 交于点O . 则 的面积与 面积的大小关系为: (填“>”,“=”或“<”).
24. 如图所示,在正方形网格中,点A , B , C , D为网格线的交点,线段 与 交于点O . 则 的面积与 面积的大小关系为: (填“>”,“=”或“<”). 25. 我们知道,给出两边及其中一边的对角的三角形不一定是唯一的.例如 中, , , ,我们可以作 ,截取 ,以B为圆心,6为半径作弧,与射线 交于点 , ,则 和 均为满足条件的三角形.已知,平行四边形 中, , , 边上的高为12,则平行四边形 面积为 .
25. 我们知道,给出两边及其中一边的对角的三角形不一定是唯一的.例如 中, , , ,我们可以作 ,截取 ,以B为圆心,6为半径作弧,与射线 交于点 , ,则 和 均为满足条件的三角形.已知,平行四边形 中, , , 边上的高为12,则平行四边形 面积为 .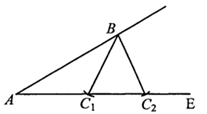
三、计算题
-
26. 在 Rt△ABC 中,∠C=90°,∠A、∠B、∠C 的对边分别为 a、b、c . 若 a∶c=15∶17,b=24,求 a.27. 如图,已知在△ABC中,CD⊥AB于D , AC=20,BC=15,DB=9.求AB的长.

四、解答题


