初中数学浙教版八年级上册2.6 直角三角形 同步练习
试卷更新日期：2021-07-02 类型：同步测试
一、单选题
-
1. 已知直角三角形中30°角所对的直角边为2cm，则斜边的长为（ ）A、2cm B、4cm C、6cm D、8cm2. 如图，在 中， ， ， ，则 的度数为（ ）
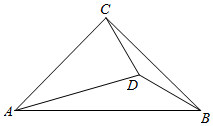A、12° B、13° C、14° D、15°3. 一副三角板如图方式摆放，点D在直线EF上，且AB//EF，则∠ADE的度数是（ ）
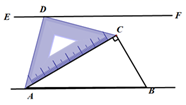A、105° B、75° C、60° D、45°4. 如图所示，在正五边形 中，过顶点A作 ，垂足为点F，连接对角线 ，则 的度数是（ ）
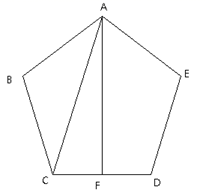A、16° B、18° C、24° D、28°5. 如图，在Rt ABC中，∠C＝90°，∠A＝30°，AB+BC＝9cm，则AB的长为（ ）
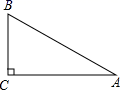A、3cm B、4cm C、5cm D、6cm6. 学校研究性学习小组的同学测量旗杆的高度．如图，在教学楼一楼地面C处测得旗杆顶部的仰角为 ，在教学楼三楼地面D处测得旗杆顶部的仰角为 ，旗杆底部与教学楼一楼在同一水平线上，已知教学楼每层楼的高度约为3.3米，则旗杆 的高度最接近（ ）
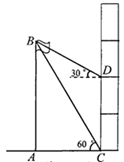A、8米 B、9米 C、10米 D、11米7. 如图，在 中， ， ，DE垂直平分AB ， 交BC于点E ， ，则 （ ）
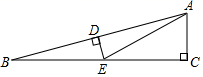A、 B、 C、 D、8. 如图，Rt△ABC中，∠C＝90°，∠B＝30°，∠BAC的平分线AD交BC于点D ， CD ，则BD的长是（ ）
A、2 B、2 C、3 D、39. 如图，在 中，点O是边 和 的垂直平分线 、 的交点，若 ，则这两条垂直平分线相交所成锐角 的度数为（ ）
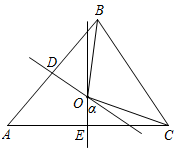A、 B、 C、 D、10. 如图： ．按下列步骤作图：①在射线 上取一点C ， 以点O为圆心， 长为半径作圆弧 ，交射线 于点F ． 连结 ；②以点F为圆心， 长为半径作圆弧，交弧 于点G；③连结 、 ．作射线 ．根据以上作图过程及所作图形，下列结论中错误的是（ ）
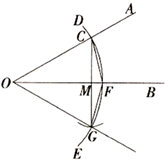A、 B、 垂直平分 C、 D、11. 如图，在等边△ABC中，点D和点B关于直线AC对称，连接CD，过D作DE⊥BC，交BC的延长线于点E，若CE＝5，则BE的长为（ ）
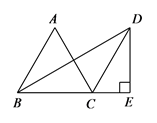A、10 B、15 C、 D、12. 如图， ，将一个含 角的直角三角尺按如图所示的方式放置，若 的度数为 ，则 的度数为（ ）
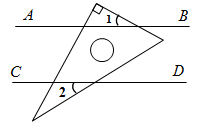A、 B、 C、 D、13. 如图，Rt△ABC中， 于点D则下列结论不一定成立的是（ ）
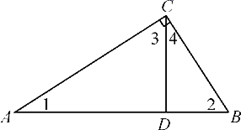A、 B、 C、 D、14. 如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于（ ）
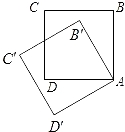A、1﹣ B、1﹣ C、 D、15. 如图，在△ABC中，∠C＝60°，AD是BC边上的高，点E为AD的中点，连接BE并延长交AC于点F．若∠AFB＝90°，EF＝2，则BF长为（ ）
A、4 B、6 C、8 D、10二、填空题
-
16. 如图，在 中，点E在 上，且 平分 ，若 ， ，则 的面积为.
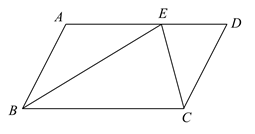17. 如图，点D是∠ABC内一点，点B在射线BA上，且∠DBE=∠BDE=15°，DE∥BC，过点D作DF⊥BC，垂足为点F，若BE=10，则DF= ．
18. 如图，已知直线a∥b，c⊥d，∠1=36°，则∠2的度数是.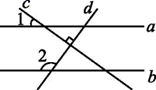
19. 如图，在Rt△ABC中，∠C=90°，∠BAC=40°，将Rt△ABC绕点A旋转得到Rt△AB'C'，且点C'落在AB上，则∠B'BC的度数为
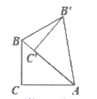20. 如图，AB是一座办公大楼，一架无人机从C处测得楼顶部B的仰角为60°，测得楼底部A的俯角为37°，测得与大楼的水平距离为40米，则该办公大楼的高度是米．（结果保留整数，参考数据： ≈1.73，sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
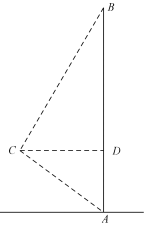21. 将一副三角尺按图所示的方式叠放在一起，如果AF= ，那么AB= ．
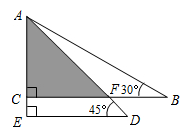22. 如图，在△ABC中，∠ACB=90°．CD为AB边上的中线，若∠A =55°，则∠BCD的度数为 ．
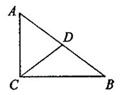23. 如图，△ABC中，AB＝AC，∠BAC＝120°，AD⊥AC交BC于点D，AD＝3，则BC＝ ．
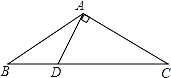24. 将一副含30°角和含45°角的三角板如图放置，则∠1的度数为度.
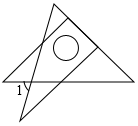25. 如图等边三角形ABC中，点O是△ABC的∠B和∠C的角平分线的交点，∠FOG=120°，绕点O旋转∠FOG，分别交线段AB、BC于点D、E两点，连接DE，若OA=2，则△ODE周长最小值为.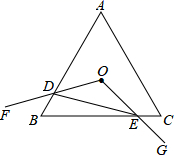
三、计算题
-
26. 如图，在△ABC中，AB=AC，AD⊥BC于点D.
(1)、若∠C=42°，求∠BAD的度数；(2)、若点E在边AB上，EF∥AC交AD的延长线于点F.求证：AE=FE.
四、解答题
-
27. 如图，已知∠AGH=∠B， ∠CGH=∠BEF，EF⊥AB于F，试说明CG⊥AB.
28. 在等边△ABC中，点D ， E分别在边BC ， AC上，若CD＝2，过点D作DE∥AB ， 过点E作EF⊥DE ， 交BC的延长线于点F ， 求EF的长．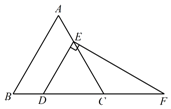
29. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝3，AD是△ABC的角平分线，DE⊥AB于点E，连接CE.求CE的长；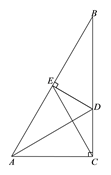
五、综合题
-
30. 等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F.
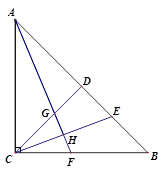(1)、求证：△ADG≌△CDE.(2)、若点H恰好为CE的中点，求证：∠CGF=∠CFG.31. 已知，△ABC是边长为3cm的等边三角形，动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．请分别解决下面四种情况：
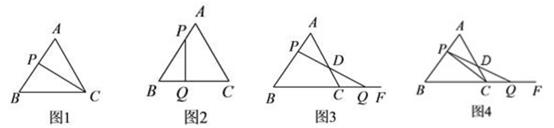(1)、如图1，设点P的运动时间为t(s)，那么t=s时，△PBC是直角三角形；(2)、如图2，若另一动点Q从点B出发，沿线段BC向点C运动，如果动点P、Q都以1cm／s的速度同时出发，设运动时间为t(s)，那么t为何值时，△PBQ是直角三角形?(3)、如图3，若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D，如果动点P、Q都以1cm／s的速度同时出发，设运动时间为t(s)，那么t为何值时，△DCQ是等腰三角形?(4)、如图4，若另一动点Q从点C出发，沿射线BC方向运动，连接PQ交AC于D，连接PC，如果动点P、Q都以1cm/s的速度同时出发．请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系?并说明理由．
-