初中数学浙教版八年级上册2.4 等腰三角形的判定定理 同步练习
试卷更新日期:2021-07-02 类型:同步测试
一、单选题
-
1. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )
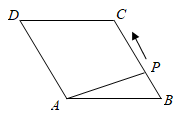 A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形2. 如图,直线a∥b,点A在直线b上,以点A为圆心,2cm长度为半径画弧,分别交直线a,b于C,B两点,连接AC,BC。若∠1=60°,则△ABC的周长为( )
A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形2. 如图,直线a∥b,点A在直线b上,以点A为圆心,2cm长度为半径画弧,分别交直线a,b于C,B两点,连接AC,BC。若∠1=60°,则△ABC的周长为( )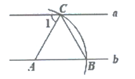 A、 cm B、2cm C、2 cm D、6cm3. 如图,Rt△ABC中,∠C=90°,∠B=30°,∠BAC的平分线AD交BC于点D , CD ,则BD的长是( )
A、 cm B、2cm C、2 cm D、6cm3. 如图,Rt△ABC中,∠C=90°,∠B=30°,∠BAC的平分线AD交BC于点D , CD ,则BD的长是( ) A、2 B、2 C、3 D、34. 如图,线段 OA绕点O旋转,线段 OB的位置保持不变,在AB的上方作等边△PAB,若 OA=1,OB=3,则在线段 OA旋转过程中,线段 OP的最大值是
A、2 B、2 C、3 D、34. 如图,线段 OA绕点O旋转,线段 OB的位置保持不变,在AB的上方作等边△PAB,若 OA=1,OB=3,则在线段 OA旋转过程中,线段 OP的最大值是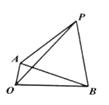 A、 B、4 C、2 D、55. 如图,在 ABC中,∠CAB=70°,在同一平面内,将 ABC绕点A旋转到 的位置.使得 ,则旋转角为( )
A、 B、4 C、2 D、55. 如图,在 ABC中,∠CAB=70°,在同一平面内,将 ABC绕点A旋转到 的位置.使得 ,则旋转角为( )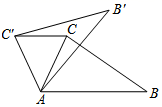 A、30° B、40° C、50° D、80°6. 下列三角形中,等腰三角形的个数是( )
A、30° B、40° C、50° D、80°6. 下列三角形中,等腰三角形的个数是( )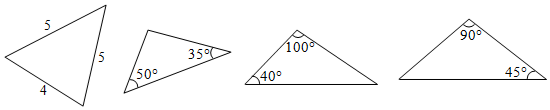 A、4个 B、3个 C、2个 D、1个7. 如图,已知∠MON及其边上一点A.以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C.再以点C为圆心,AC长为半径画弧,恰好经过点B.错误的结论是( )
A、4个 B、3个 C、2个 D、1个7. 如图,已知∠MON及其边上一点A.以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C.再以点C为圆心,AC长为半径画弧,恰好经过点B.错误的结论是( )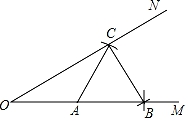 A、S△AOC=S△ABC B、∠OCB=90° C、∠MON=30° D、OC=2BC8. 如图,AC , BD相交于点O , ∠A=∠D . 若请你再补充一个条件,使得△BOC是等腰三角形,则你补充的条件不能是( )
A、S△AOC=S△ABC B、∠OCB=90° C、∠MON=30° D、OC=2BC8. 如图,AC , BD相交于点O , ∠A=∠D . 若请你再补充一个条件,使得△BOC是等腰三角形,则你补充的条件不能是( )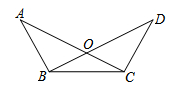 A、OA=OD B、AB=CD C、∠ABO=∠DCO D、∠ABC=∠DCB9. 点P是等边三角形ABC所在平面上一点,若P和△ABC的三个顶点所组成的△PAB , △PBC , △PAC都是等腰三角形,则这样的点P的个数为( )A、1 B、4 C、7 D、1010. 如图,在等腰 与等腰 中, , , ,连接 和 相交于点 ,交 于点 ,交 与点 .则下列结论:① ;② ;③ 平分 ;④若 ,则 .一定正确的是( )
A、OA=OD B、AB=CD C、∠ABO=∠DCO D、∠ABC=∠DCB9. 点P是等边三角形ABC所在平面上一点,若P和△ABC的三个顶点所组成的△PAB , △PBC , △PAC都是等腰三角形,则这样的点P的个数为( )A、1 B、4 C、7 D、1010. 如图,在等腰 与等腰 中, , , ,连接 和 相交于点 ,交 于点 ,交 与点 .则下列结论:① ;② ;③ 平分 ;④若 ,则 .一定正确的是( )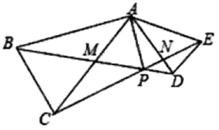 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
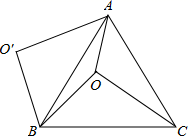
11. 如图, 是正 内一点, , , ,将线段 以点 为旋转中心逆时针旋转60°得到线段 ,下列结论:① 可以由 绕点 逆时针旋转60°得到;②点 与 距离为4;③ ;④ ;⑤ .其中正确的结论是 .
 12. 如图,在正方形ABCD的外侧作等边三角形CDE , 则∠AED的度数为 .
12. 如图,在正方形ABCD的外侧作等边三角形CDE , 则∠AED的度数为 .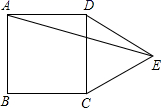 13. 如图,在 中, , ,BD平分 ,CD平分 , ,且EF过点D,则 的周长是.
13. 如图,在 中, , ,BD平分 ,CD平分 , ,且EF过点D,则 的周长是.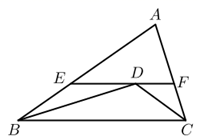 14. 如图,△ABC中,点O是AB边上的一个动点,过点O做直线MN∥BC,直线MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,设OC的长为x,EF的长为y,那么y关于x的函数关系式是
14. 如图,△ABC中,点O是AB边上的一个动点,过点O做直线MN∥BC,直线MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,设OC的长为x,EF的长为y,那么y关于x的函数关系式是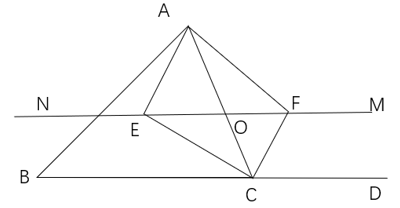 15. 在等腰△ABC 中,AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC,则△ABC 的顶角的度数为16. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△AʹBʹCʹ,连接AʹC , 则△AʹBʹC的周长为 .
15. 在等腰△ABC 中,AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC,则△ABC 的顶角的度数为16. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△AʹBʹCʹ,连接AʹC , 则△AʹBʹC的周长为 .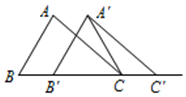
三、计算题
-
17. 如图, , , .
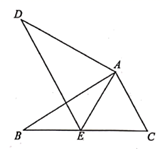 (1)、求证: ;(2)、若 ,求 的长.
(1)、求证: ;(2)、若 ,求 的长.四、解答题
-
18. 在①AD=AE,②∠ABE=∠ACD,③FB=FC 这三个条件中选择其中一个 , 补充在下面的问题中,并完成问题的解答。
问题:如图,在△ABC中,∠ABC=∠ACB,点D在AB边上(不与点A,点B重合),点E在AC边上(不与点A,点C重合),连结BE,CD,BE与CD相交于点F。若_▲_,求证:BE=CD 。
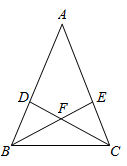
注:如果选择多个条件分别作答,按第一个解答计分。
五、综合题
-
19. 如图,在四边形ABCD中,AB=AD=20,BC=DC=10 .
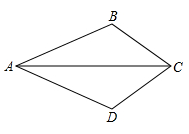 (1)、求证:△ABC≌△ADC;(2)、当∠BCA=45°时,求∠BAD的度数.20. 如图
(1)、求证:△ABC≌△ADC;(2)、当∠BCA=45°时,求∠BAD的度数.20. 如图 (1)、问题发现:如图1,如果 和 均为等边三角形 等边三角形的三条边都相等,三个角都是 ,点B、E、D三点在同一直线上,连接 则CD与BE的数量关系为; 的度数为度.(2)、探究:如图2,若 为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边 与等边 ,连接BE和CD相交于点O , AB交CD于点F , AC交BE于G , 则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出 的度数?21. 如图①,在△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB, ,垂足E在 CD的延长线上. 求证∶ .
(1)、问题发现:如图1,如果 和 均为等边三角形 等边三角形的三条边都相等,三个角都是 ,点B、E、D三点在同一直线上,连接 则CD与BE的数量关系为; 的度数为度.(2)、探究:如图2,若 为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边 与等边 ,连接BE和CD相交于点O , AB交CD于点F , AC交BE于G , 则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出 的度数?21. 如图①,在△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB, ,垂足E在 CD的延长线上. 求证∶ .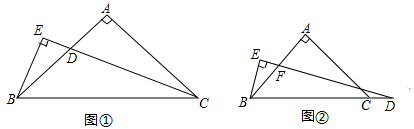 (1)、观察分析∶延长 BE,CA,交于点 F.可证明△_ △ , 依据是; 从而得到;再证 .(2)、类比探究∶如图②,在△ABC中,AB=AC,∠BAC=90°,点 D在线段 BC上, ,垂足为E,DE与AB相交于点F. 试探究BE与DF的数量关系,并证明你的结论.
(1)、观察分析∶延长 BE,CA,交于点 F.可证明△_ △ , 依据是; 从而得到;再证 .(2)、类比探究∶如图②,在△ABC中,AB=AC,∠BAC=90°,点 D在线段 BC上, ,垂足为E,DE与AB相交于点F. 试探究BE与DF的数量关系,并证明你的结论.
-
-