初中数学浙教版八年级上册2.3 等腰三角形的性质定理同步练习

试卷更新日期：2021-07-02 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，等腰三角形ABC中，AB＝AC，∠A＝46°，CD⊥AB于点D，则∠DCB＝（）

A、46° B、67° C、44° D、23°

查看试题解析
2. 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E。若∠E=35°，则∠EAC的度数是（）

A、40° B、65° C、70° D、75°

查看试题解析
3. 如图，在△ABC中，BA＝BC ， ∠B＝80°，观察图中尺规作图的痕迹，则∠DCE的度数为（　　）

A、60° B、65° C、70° D、75°

查看试题解析
4. 如图， $A B$ ∥ $C D$ ， $A D = C D$ ， $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数是（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
5. 如图，在 $△ A B C$ 中，已知∠B＝50°，∠C＝30°.分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点E，F，作直线EF，交BC于点D，连接AD，则∠BAD的度数为（）

A、70° B、60° C、55° D、45°

查看试题解析
6. 如图△ABC中，AB＝AC，∠BAC＝120°，BC＝2 $\sqrt{3}$ ，D为BC的中点，DE⊥AB，则△EBD的面积为（）

A、 $\frac{3 \sqrt{3}}{4}$ B、 $\frac{3 \sqrt{3}}{8}$ C、 $\frac{\sqrt{3}}{4}$ D、 $\frac{\sqrt{3}}{8}$

查看试题解析
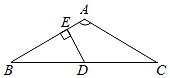7. 如图， $△ A B C$ 中，AB＝AC，AD⊥BC于点D，DE⊥AB于点E，BF⊥AC于点F，DE＝2，则BF的长为（）

A、4 B、3 C、5 D、6

查看试题解析
8. 直线 $y = x - 1$ 与坐标轴交于 $A$ 、 $B$ 两点，点 $C$ 在坐标轴上， $Δ A B C$ 为等腰三角形，则满足条件的点 $C$ 最多有（）个

A、8； B、4； C、5； D、7.

查看试题解析
9. 等腰三角形的一个角是 50°，则它的底角的度数为（）

A、50° B、50°或 80° C、50°或 65° D、65°

查看试题解析
10. 如图，在△ABC中，AB=AC，BD 平分∠ABC 交AC 平点D，AE∥BD 交CB 的延长线于点E。若∠E=35°，则∠BAC 的度数为（）

A、40° B、45° C、60° D、70°

查看试题解析
11. 如图，C，E是直线l两侧的点，以C为圆心，CE长为半径画弧交l于A，B两点，又分别以A，B为圆心，大于 AB的长为半径画弧，两弧交于点D，连接CA，CB，CD，下列结论不一定正确的是（）

A、CD⊥l B、点A，B关于直线CD对称 C、点C，D关于直线l对称 D、CD平分∠ACB

查看试题解析
12. 若一个等腰三角形的两边长分别是2和5，则它的周长为（）

A、12或9 B、9 C、12 D、9或7

查看试题解析
13. 如图，在△ABC中，按以下步骤作图：①分别以A，B为圆心，大于 $\frac{1}{2}$ AB长为半径作弧，两弧相交于M，N两点；②作直线MN交BC于点D，连接AD.若AD=AC，∠B=25°，则∠C=（）

A、70° B、60° C、50° D、40°

查看试题解析
14. 如图，在 $△ A B C$ 中，按以下步骤作图：①分别以 $B$ ， $C$ 为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于两点 $M$ ， $N$ ；②作直线 $M N$ 交 $A B$ 于点 $D$ ，连接 $C D$ .若 $C D = A C$ ， $∠ A = 50^{\circ}$ ，则 $∠ A C B$ 的度数为（）

A、 $95^{\circ}$ B、 $100^{\circ}$ C、 $105^{\circ}$ D、 $110^{\circ}$

查看试题解析
15. 如图，在已知的△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD.若AD＝AC，∠A＝80°，则∠ACB的度数为（）

A、65° B、70° C、75° D、80°

查看试题解析

二、填空题

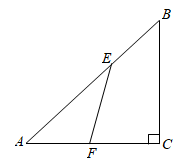
16. 如图.在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A F = E F$ .若 $∠ C F E = 72 °$ ，则 $∠ B =$ .

查看试题解析
17. 如图，在△ABC中，∠ACB＝90°，AC＜BC.分别以点A，B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF.以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH.若BC＝3，则△AFH的周长为 .

查看试题解析
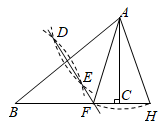18. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B = 70 °$ ，以点C为圆心，CA长为半径作弧，交直线BC于点P，连结AP，则 $∠ B A P$ 的度数是.

查看试题解析
19. 已知等腰三角形的两边长分别为4cm和6cm，则这个等腰三角形的周长为cm

查看试题解析
20. 如图， $E A = E B = E C$ ， $∠ A E B = 70 °$ ，∠BEC=40°，则 $∠ A C B =$ °．

查看试题解析
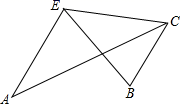21. 如图，∠PAQ＝36°，点B为射线AQ上一点，AB＝5cm ，按以下步骤作图，第一步：分别以点A ， B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点M ， N；第二步：作直线MN交射线AP于点D ，连接BD；第三步：以点B为圆心，BA的长为半径画弧，交射线AP于点C ，连接BC ，线段CD的长为cm ．

查看试题解析
22. 若等腰三角形一腰上的高等于腰长的一半，则此等腰三角形的二个底角的度数等于度．

查看试题解析
23. 如图，在△ABC中，AB＝AC＝8，∠BAC＝120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点F，则DF的长为．

查看试题解析
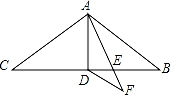24. 如图，△ABC中，∠B，∠C的平分线相交于点F，过F作DE∥BC，分别交AB、AC于D、E，若AB+AC＝10，则△ADE的周长等于．

查看试题解析
25. 如图，在△ABC中，AB＝AC，BD⊥AC，垂足为点D．若∠BAC＝30°，则∠DBC的度数为 °．

查看试题解析

三、计算题

26. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 在边 $B C$ 上，且 $B D = A B$ ，连接 $A D$ ，若 $A D = C D$ ，求 $∠ B$ 的度数．

查看试题解析
27. 已知：如图，在△ABC中，AB=AC，点D，E在边BC上，且BD=CE．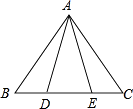
求证：AD=AE．

查看试题解析

四、解答题

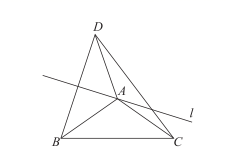
28. 如图，在等腰△ABC中，AB=AC ，直线l过点A．点B与点D关于直线l对称，连接AD ， CD ．求证：∠ACD=∠ADC ．

查看试题解析
29. 如图，在△ABC中，AB＝AC，点D是BC的中点，点E在AB上，BE＝BD，∠BAC＝80°，求∠ADE的大小．

查看试题解析

五、综合题

30. 已知：如图①，直线l和l外一点P.求作：直线l的垂线，使它经过点P.
作法：如图②，

（ 1 ）在直线l上任取一点A；（2）连接AP，以点P为圆心，AP长为半径作弧，交直线l于点B（点A，B不重合）；（3）连接BP，作∠APB的平分线，交AB于点H，所以直线PH就是所求作的垂线.

根据上面的作法，完成以下问题：

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明.
证明：∵PH平分∠APB，

∴∠APH=▲.

∵PA=▲ ，

∴PH⊥直线l于H.（）（填推理的依据）

查看试题解析

初中数学浙教版八年级上册2.3 等腰三角形的性质定理 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

初中数学浙教版八年级上册2.3 等腰三角形的性质定理同步练习