天津市滨海新区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-02 类型：期末考试

进入出卷网下载

一、选择题(本大题共12小题，每小题3分，共36分. 在每小题给出的四个选项中，只有一项是符合题目要求的)

1. 3的算术平方根是（）

A、 $\sqrt{3}$ B、－ $\sqrt{3}$ C、 $\pm \sqrt{3}$ D、9

查看试题解析
2. 平面直角坐标系中，在第三象限的点是（）

A、（－3，5） B、（1，－2） C、（－2，－3） D、（1，1）

查看试题解析
3. 估计 $\sqrt{41}$ 的值在（）

A、5与6之间 B、6与7之间 C、7与8之间 D、8与9之间

查看试题解析
4. 在实数－ $\sqrt{5}$ ， $0 . \overset{\cdot}{4} 2 \overset{\cdot}{1}$ ，3.14，0， $\frac{π}{2}$ ， $\frac{22}{7}$ ， $\sqrt{81}$ ，0.1616616661……（两个1之间依次多一个6）中，无理数的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
5. 如图，AB⊥CD于D ， DE⊥DF ，若∠BDE = 60°，则∠CDF为（）

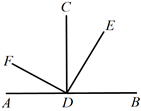A、30° B、45° C、60° D、120°

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{{(- 6)}^{2}}$ =-6 B、 $\sqrt[3]{- 27}$ =3 C、 $- \sqrt{9}$ =3 D、 $\pm \sqrt{16} = \pm 4$

查看试题解析
7. 如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）

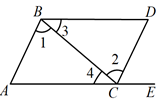A、∠1 = ∠2 B、∠3 = ∠4 C、∠D＋∠ACD = 180° D、∠D = ∠DCE

查看试题解析
8. 下列调查中，不适合采用全面调查方式的是（）

A、了解新冠肺炎确诊病人同机乘客的身体健康情况 B、对我市中学生每周课外阅读时间情况的调查 C、对全校同学进行每日温度测量统计 D、调查某中学在职教师的年龄分布情况

查看试题解析
9. 如果 a＞b ，那么下列不等式中一定成立的是（）

A、 $a - 3 > b + 3$ B、 $\frac{a}{2} < \frac{2}{b}$ C、 $a c > b c$ D、 $- a + 2 < - b + 2$

查看试题解析
10. 下列命题为真命题的是（）

A、相等的角是对顶角 B、同一平面内，垂直于同一条直线的两条直线平行 C、过一点有且只有一条直线与已知直线平行 D、两条直线被第三条直线所截，同位角相等

查看试题解析
11. 现用190张铁皮做盒子，每张铁皮可做8个盒身，或做22个盒底，一个盒身与两个盒底配成一个盒子．设用 x 张铁皮做盒身， y 张铁皮做盒底正好配套．则可列方程组为（）

A、 $\{\begin{cases} x + y = 190 \\ 2 \times 8 x = 22 y \end{cases}$ B、 $\{\begin{cases} x + y = 190 \\ 2 \times 22 y = 8 x \end{cases}$ C、 $\{\begin{cases} 2 y + x = 190 \\ 8 x = 22 y \end{cases}$ D、 $\{\begin{cases} 2 y + x = 190 \\ 2 \times 8 x = 22 y \end{cases}$

查看试题解析
12. 关于x的不等式组 ${\begin{matrix} x - a \geq 0 \\ 2 x - b < 0 \end{matrix}$ 的整数解为x =1和x=2 ，若a ， b为整数，则a+b的值是（）

A、5 B、6 C、5或6 D、6或7

查看试题解析

二、填空题(本大题共6小题，每小题3分，共18分)

13. $- \sqrt{5}$ 的相反数为.

查看试题解析
14. 如图，直线AB、CD相交于点O ，

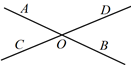
若∠AOC+∠BOD =100°，则∠AOD =° .

查看试题解析
15. 若点M（m-1，m+5）在y轴上，则点M的坐标是 .

查看试题解析
16. 如图是30名学生数学成绩的频数分布直方图，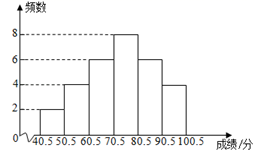

如图可知40.5~50.5这一分数段的频数为2，

组距是，组数是，

70.5~80.5分数段的频数是．

查看试题解析
17. 如图，在平面直角坐标系中，线段AB平移至线段CD ，连接AC ， BD ．若点B（－2，－2）的对应点为D（1，2），则点A（－3，0）的对应点C的坐标是．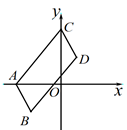

查看试题解析
18. 将长为4，宽为 a （ a 大于2且小于4）的长方形纸片按如图①所示的方式折叠并压平，剪下一个边长等于长方形宽的正方形，称为第一次操作；再把剩下的长方形按如图②所示的方式折叠并压平，剪下边长等于此时长方形宽的正方形，称为第二次操作；如此反复操作下去…，若在第n次操作后，剩下的长方形恰为正方形，则操作终止．当 n=3 时， a 的值为．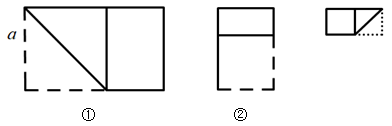

查看试题解析

三、解答题(本大题共7小题，共66分．解答应写出文字说明、演算步骤或证明过程)

19. 解方程组：

(1)、 $\{\begin{cases} y = 10 - x \\ 2 x + y = 16 \end{cases}$

(2)、 $\{\begin{cases} 4 x - y = 3 \\ 3 x + 2 y = 5 \end{cases}$

查看试题解析
20. 解不等式组 $\{\begin{cases} \frac{5}{2} x + 1 \geq \frac{3}{2} x \\ x - 2 \leq 6 - 3 x \end{cases}$
请结合题意填空，完成本题的解答．

（Ⅰ）解不等式①，得       ▲         ；

（Ⅱ）解不等式②，得        ▲         ；

（Ⅲ）把不等式①和②的解集在数轴上表示出来：



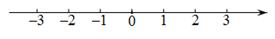
（Ⅳ）原不等式组的解集为       ▲          ．

查看试题解析
21. 完成下面的推理，并在括号内标注理由：
如图，已知AD⊥BC ， EG⊥BC ，垂足分别为D ， G ，且∠1=∠3，∠C= 52°．
求∠FDC的度数．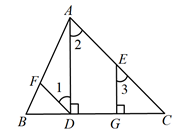

解：∵ AD⊥BC ， EG⊥BC ，

∴ ∠ADC =∠EGC =    ▲   ° （   ▲   ）．

∴ AD∥EG ．

∴ ∠2=∠3 （   ▲   ）．

∵ ∠1=∠3，

∴ ∠1=∠2 （   ▲   ）．

∴ DF∥   ▲   （   ▲   ）．

∴ $∠ C +$ ∠FDC = 180°（   ▲   ）．

∵ ∠C= 52°，

∴ ∠FDC =   ▲   ．

查看试题解析
22. 网络学习越来越受到学生的青睐，某校为学生提供了四种课后辅助学习方式：A网上测试，B网上阅读，C网上答疑，D网上讨论．为了解学生对四种学习方式的喜欢情况，该校随机抽取部分学生进行问卷调查，被调查学生需从四种方式中选择自己最喜欢的一种，根据调查结果绘制成如图两幅不完整的统计图：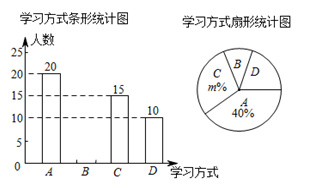

根据统计图提供的信息，解答下列问题：

(1)、本次共调查了名学生；

(2)、在扇形统计图中，m的值是，
学习方式D对应的扇形圆心角的

度数是度；

(3)、根据以上信息直接在答题卡中补全条形统计图；

(4)、根据抽样调查的结果，请你估计该校800名学生中最喜欢方式D的学生人数．

查看试题解析
23. 如图，在四边形ABCD中，点E为AB延长线上一点，点F为CD延长线上一点．连接EF ，交BC于点G ，交AD于点H ，若∠1=∠2，∠A=∠C ．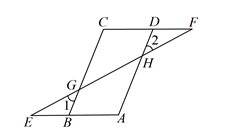

求证：∠E=∠F ．

查看试题解析
24. 为配合城市“花博会”，花农黄老伯培育了甲、乙两种花木各若干株．如果培育甲、乙两种花木各一株，那么共需成本500元；如果培育甲种花木3株和乙种花木2株，那么共需成本1200元．

(1)、求甲、乙两种花木每株的培育成本分别为多少元？

(2)、市场调查显示，甲种花木的市场售价为每株300元，乙种花木的市场售价为每株500元．如果黄老伯培育这些花木总利润不少于18000元，培育的乙种花木的数量比甲种花木的数量的3倍少10株，那么黄老伯至少培育甲种花木多少株？

查看试题解析
25. 在平面直角坐标系中，O为原点，点A(a ， 0)，B(c ， c)，C(0，c)，且满足 ${(a + 8)}^{2} + \sqrt{c + 4} = 0$ ，P点从A点出发沿 x 轴正方向以每秒2个单位长度的速度匀速移动，同时Q点从 $O$ 点出发沿y轴负方向以每秒1个单位长度的速度匀速移动．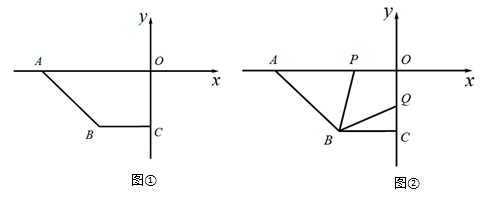

(1)、如图①，直接写出点B的坐标， AO和BC位置关系是；

(2)、如图②，当P ， Q分别在线段AO ， OC上时，连接PB ， QB ，使三角形PAB的面积是三角形QBC面积的2倍，求点P的坐标．

(3)、在P ， Q的运动过程中，当 $∠ C B Q = 30^{\circ}$ 时，请直接写出 $∠ O P Q$ 和 $∠ P Q B$ 的数量关系．

查看试题解析

天津市滨海新区2020-2021学年七年级下学期数学期末试卷

一、选择题(本大题共12小题，每小题3分，共36分. 在每小题给出的四个选项中，只有一项是符合题目要求的)

二、填空题(本大题共6小题，每小题3分，共18分)

三、解答题(本大题共7小题，共66分． 解答应写出文字说明、演算步骤或证明过程)

三、解答题(本大题共7小题，共66分．解答应写出文字说明、演算步骤或证明过程)