江西省南昌市2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-02 类型：期末考试

进入 出卷网 下载

一、选择题（本大题6小题，每小题3分，共18分，每小题只有一个正确选项）

  • 1. 实数4- 2 的值在（     ）
    A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

    查看试题解析

  • 2. 如图，已知a∥b ， 直角三角板的直角顶点在直线b上，则下列结论错误的是（ 　　）

    A、∠2＝∠5 B、∠4-∠5＝90°                                      C、∠1+∠5＝90° D、∠4+∠1＝180°

    查看试题解析

  • 3. 已知点M（1﹣m ， m﹣3），则点M不可能在（　 　）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 4. 足球比赛规定：胜一场得3分，平一场得1分，负一场得0分．某足球队共进行了6场比赛，得了12分，该队获胜的场数可能是（　　）
    A、1或2 B、2或3 C、3或4 D、4或5

    查看试题解析

  • 5. 已知不等式组x-3>0x+1⩾0 ， 其解集在数轴上表示正确的是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 6. 如图所示，某校七年级（1）班的全体同学最喜欢的球类运动用的扇形统计图来表示，下面说法中错误的是（     ）

    A、喜欢排球的占全班的总人数的 115 B、喜欢乒乓球的占全班的总人数的 14 C、喜欢足球的人数最多 D、喜欢足球的人数是喜欢篮球的人数的2倍

    查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

  • 7. 计算： 4 = ．

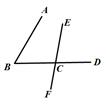
    查看试题解析

  • 8. 如图，“4”字图中有a对同位角，b对内错角，c对同旁内角，则abc= ．

    查看试题解析

  • 9. 已知点A(a ， 20)向下平移a个单位得到点A′(21，b)，则b＝ ．

    查看试题解析

  • 10. 《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”译文：“现在有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，可列方程组为 ．

    查看试题解析

  • 11. 不等式组 {x>−1x<m 有且只有3个整数解，则m的取值范围是 ．

    查看试题解析

  • 12. 已知整数x ， y满足 |x−5|+y−3=1 ，则x ， y的值= ．

    查看试题解析

三、（本大题共5小题，每小题6分，共30分）

  • 13.        
    (1)、解二元一次方程组： {x−y=2x−y=y+1 ．  
    (2)、解不等式： x−2≥x+12+3 ．

    查看试题解析

  • 14. 解不等式组： {5x−1<3(x+1)2x−13−1≤5x+12 ．

    查看试题解析

  • 15. 已知直线 l1 ，请按下列要求分别画出示意图 ．

    ⑴在图1中，画出直线 l2 ， l3 ，使它们只有1个交点；

    ⑵在图2中，画出直线 l2 ， l3 ，使它们只有2个交点；

    ⑶在图3中，画出直线 l2 ， l3 ，使它们只有3个交点．

    查看试题解析

  • 16. 图1是某品牌的商标，图2是该商标的示意图．已知：AB∥DE ， BC∥EF ， CD∥FA.

    (1)、写出图中所有相等的角；
    (2)、证明（1）中一对相等的角.

    查看试题解析

  • 17. 魏茹丽同学本学期由于努力学习，数学成绩稳步提高 ．

    下表为魏茹丽同学本学期近五次数学考试成绩：

    序 号

    1

    2

    3

    4

    5

    数学成绩

    80

    85

    85

    90

    90

    (1)、补全折线统计图
    (2)、已知第6次测验的难度与前5次相当，请你预测一下她的这次数学成绩，并说明你的预测理由(言之有理即可).

    查看试题解析

四、

  • 18. 已知关于x ， y的二元一次方程组 {x+y=5m−5x−y=m+1
    (1)、写出一个不含m的关于x ， y的二元一次方程；
    (2)、解这个方程组（用含m式子表示）；
    (3)、若方程组的解（x ， y）在第四象限，求整数m的值.

    查看试题解析

  • 19. 某校为了了解本校学生对中国民族乐器的喜爱情况，随机抽取了本校的部分学生进行调查（每名学生选择并且只能选择一种最喜爱的乐器），现将收集到的数据绘制成如下两幅不完整的统计图．

    (1)、这次一共抽取了名学生进行调查，扇形统计图中的“竹笛”x＝（填百分数）；
    (2)、在扇形统计图中“二胡”所对扇形的圆心角是度；请补全条形统计图；
    (3)、若该校有3000名学生，请你估计该校喜爱“扬琴”的学生约有多少名．

    查看试题解析

  • 20. 荔枝的品种有许多种，其中桂味、糯米糍是荔枝口感上佳的品种．显赫奶奶先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了3千克桂味和2千克糯米糍，共花费85元．（每次购买两种荔枝的售价都不变）
    (1)、购买了1千克桂味荔枝比1千克糯米糍荔枝少花费元；
    (2)、求桂味荔枝和糯米糍荔枝的售价分别是每千克多少元；
    (3)、如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．

    查看试题解析

五、（本大题2小题，每小题9分，共18分）

  • 21. 如图，四条街围成边长为1000m的正方形ABCD显然家住在东西方向DA街道的点P处，他的学校在东西方向CB街道的点Q处．已知显然爷爷骑电动车在东西方向的街道的速度是400m/min，在南北方向的街道的速度是500m/min．已知爷爷骑电动车沿P-A-B-Q送显然上学花了5min，沿Q-B-C-D-P（在B处遇堵车立即掉头）回家花了6min.

    (1)、爷爷骑电动车跑一圈需要多少min？
    (2)、求PA ， QB的长度；
    (3)、如果爷爷和显然同时出发，爷爷骑电动车沿P-A-B-Q骑行，显然沿Q-B步行，且在BQ上互相看见，求显然步行的速度的取值范围.

    查看试题解析

  • 22. 如图，点A（1，n），B（n ， 1），我们定义：将点A向下平移1个单位，再向右平移1个单位，同时点B向上平移1个单位，再向左平移1个单位称为一次操作，此时平移后的两点记为A1 ， B1 ， t次操作后两点记为At ， Bt ． .

    (1)、直接写出A1 ， B1 ， At ， Bt的坐标（用含n、t的式子表示）；
    (2)、以下判断正确的是（      ）
    A、经过n次操作，点A ， 点B位置互换 B、经过（n-1）次操作，点A ， 点B位置互换 C、经过2n次操作，点A ， 点B位置互换 D、不管几次操作，点A ， 点B位置都不可能互换
    (3)、t为何值时，At ， B两点位置距离最近？

    查看试题解析

  • 23. 我市某学校抽样调查该校学生从家里到学校的出行方式，A类学生：骑共享单车；B类学生：坐公交车、私家车、网约车等；C类学生：步行；D类学生：其它方式．根据抽样调查结果绘制了不完整的统计表和条形统计图．

    类型

    频数

    频率

    A

    30

    z

    B

    18

    0.15

    C

    m

    x

    D

    n

    y

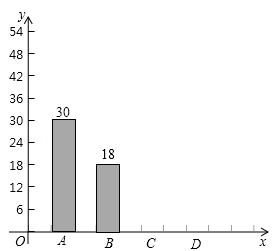    (1)、抽样调查的学生共人；
    (2)、如果x＝2y ， 列方程组求m、n的值，并补全条形统计图；
    (3)、在（2）的前提下，若对D类学生进行深入调查，发现其中有相同的人数可以分别归为A类学生、B类学生，这样A类学生人数比B类学生人数1.5倍还多，求最后划为D类学生的人数最小值．

    查看试题解析