江西省南昌市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-02 类型:期末考试
一、选择题(本大题6小题,每小题3分,共18分,每小题只有一个正确选项)
-
1. 化简: 等于( )A、2 B、±2 C、4 D、±42. 由线段a , b , c组成的三角形不能构成直角三角形的是( )A、0.6,0.8,1 B、4,5,6 C、5,12,13 D、20,21,293. 如图,正方形ABCD中,EF≠AB , 点P、Q、R、S分别是AB , BC , CD , DA上的点,有以下四个命题:

①若SQ∥EF , 则SQ=EF; ②若SQ=EF , 则SQ∥EF;
③PR⊥EF , 则PR=EF; ④PR=EF , 则PR⊥EF . 其中真命题有( )
A、①② B、③④ C、①③ D、①②③④4. 经过(1,2),(-3,-4)两点的直线不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 一年级(1)班部分同学背诵课文《人之初》的时间(单位:s)26,42,30,40,29,29,27,29,28,30
设平均数为P , 众数为Z , 中位数为W , 则( )
A、P= Z B、P=W C、Z=W D、P= Z=W6. 下列图象中,不表示某一函数图象的是( )A、 B、
B、 C、
C、 D、
D、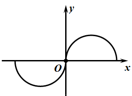
二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 若 的取值范围是 ,则a=.8. 一组数据2,0,2,1,a , 的众数只有一个,则a≠ .9. 如图,矩形ABCD中,已知:AB=3,BC=9,将矩形沿EF翻折,使点C与点A重合,点D落在点D'处,则EF=.
 10. 过点A(0,2),且与直线y=3x-4平行的直线解析式为:.11. 一组数据:1,2,2,3,3,3,4,4,4,4的平均数等于.12. 如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP=.
10. 过点A(0,2),且与直线y=3x-4平行的直线解析式为:.11. 一组数据:1,2,2,3,3,3,4,4,4,4的平均数等于.12. 如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP=.
三、(本大题共5小题,每小题6分,共30分)
-
13.(1)、计算: ;(2)、求x的值:14. 给你一组数据:1,2,3,4,5,x .(1)、如果该组数据的平均数是100,求x的值;(2)、如果该组数据的平均数等于众数x , 求x的值.15. 已知如下三个正比例函数:
y1= x , y2=kx(k≠0),y3=-2x
(1)、写出这三个正比例函数的图象都具有的一条性质;(2)、如果直线x=m(m≠0)与y1、y2、y3顺次交于点A、点B、点C , 且AB=BC , 求k的值.16. 如图,四边形ABCD中,对角线AC、BD相交于点O , 且AC⊥BD有以下结论:① ;② ;③
 (1)、以上结论中,正确的有(只要填序号即可);(2)、证明(1)中一个正确的结论.17. 如图,菱形ABCD及点P , 请仅用无刻度的直尺按要求完成下列作图.
(1)、以上结论中,正确的有(只要填序号即可);(2)、证明(1)中一个正确的结论.17. 如图,菱形ABCD及点P , 请仅用无刻度的直尺按要求完成下列作图.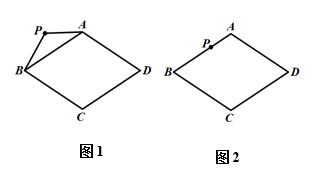 (1)、如图1,若点P在AB上,请在CD上作出点Q , 使CQ=AP;(2)、如图2,若点P在菱形ABCD外,请在菱形外作点Q , 使△CQD≌△APB.
(1)、如图1,若点P在AB上,请在CD上作出点Q , 使CQ=AP;(2)、如图2,若点P在菱形ABCD外,请在菱形外作点Q , 使△CQD≌△APB.四、(本大题3小题,每小题8分,共24分)
-
18. 如图,四边形ABCD中,已知:A(a , 0),B(0,b),C(c , 0)和D(0,d).
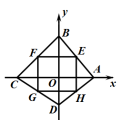 (1)、当四边形ABCD正方形时,写出a , b , c , d满足的等式关系:(2)、若AB、BC、CD、DA的中点分别为E、F、G、H.
(1)、当四边形ABCD正方形时,写出a , b , c , d满足的等式关系:(2)、若AB、BC、CD、DA的中点分别为E、F、G、H.①直接写出E、F、G、H四点的坐标;
②证明:四边形EFGH是矩形;
③若矩形EFGH是正方形,则a , b , c , d满足的等式关系是.
19. 某灯炮厂为了测量一批灯泡的使用寿命,从中抽取了50只灯泡,它们的使用寿命如下表:使用寿命x/kh
0.6≤x<1
1≤x<1.4
1.4≤x<1.8
1.8≤x<2.2
2.2≤x<2.6
组中值
0.8
1.2
2.4
灯泡只数
5
10
12
5
(1)、完成表格;(2)、求抽取的灯泡的平均使用寿命是多少kh?(3)、估计这批灯泡平均使用寿命是多少kh.20. 如图为一次函数l: 的图象. (1)、用“>”、“=”,“<”填空:k0, b0;(2)、将直线l向下平移2个单位,再向左平移1个单位,发现图象回到l的位置,求k的值;(3)、当k=3时,将直线l向上平移1个单位得到直线l1 , 已知:直线l , 直线l1 , x轴,y轴
(1)、用“>”、“=”,“<”填空:k0, b0;(2)、将直线l向下平移2个单位,再向左平移1个单位,发现图象回到l的位置,求k的值;(3)、当k=3时,将直线l向上平移1个单位得到直线l1 , 已知:直线l , 直线l1 , x轴,y轴围成的四边形面积等于1,求b的值.
五、(本大题2小题,每小题9分,共18分)
-
21. 某公司欲招聘一名销售人员,按1:3的比例入围的甲、乙、丙(笔试成绩没有相同的,按从高到低排列,)三位入围者的成绩(百分制,成绩都是整数)如下表:
入围者
笔试成绩
面试成绩
甲
90
86
乙
x
x
丙
84
92
(1)、若公司认为笔试成绩与面试成绩同等重要,结果乙被录取,求x的值;(2)、若公司认为笔试成绩与面试成绩按4:6的权重,结果乙排第二,丙被录取,求x的值;(3)、若公司认为笔试成绩与面试成绩按a:(10-a)(a为1~9的整数)的权重,为确保甲被录取,求a的最小值.22. 如图,直线 经过A(0,a),B(b , 0)两点,直线 经过C(0,c),D(d , 0)两点, , 相交于点P. (1)、求直线 的解析式(用含a , b的式子表示),直接写出 的解析式(用含c , d的式子表示);(2)、若△OAB≌△ODC , 求证: ;(3)、若P(1,1), ,求证:AB=CD.
(1)、求直线 的解析式(用含a , b的式子表示),直接写出 的解析式(用含c , d的式子表示);(2)、若△OAB≌△ODC , 求证: ;(3)、若P(1,1), ,求证:AB=CD.六、(本大题共12分)
-
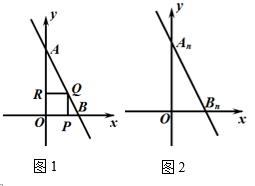
23. 如图1,直线 与y轴交于点 ,与x轴交于点 .
 (1)、按题意填表:
(1)、按题意填表:n
1
2
3
4
5
0
0
0
0
0
4
2
0
0
0
0
0
(2)、由(1)中表格中的数据可以发现:①对于 , = , = , , ;
②直线 一定经过的点的坐标为;
(3)、如图2,正方形OPQR是△ 的内接正方形,设正方形的边长为m ,求证:1<m<2.