安徽省合肥市蜀山区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-02 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 下列式子中，为最简二次根式的是（     ）
    A、12 B、2 C、0.6 D、8

    查看试题解析

  • 2. 下列各组数中，能作为直角三角形的三边长的是（       ）
    A、  1，2，3 B、  2，3，5 C、  1， 2 ， 3 D、  2 ，3，5

    查看试题解析

  • 3. 甲、乙、丙、丁四组同学参加跳绳团体赛，经过几轮测试，四组同学的平均成绩相同，方差分别为s甲2 =0.28，

    s乙2 =0.36，s丙2=0.58， s丁2=0.44，你认为哪一组同学的成绩比较稳定（       ）

    A、  甲 B、  乙 C、  丙 D、  丁

    查看试题解析

  • 4. 把方程x2-6x-1=0转化成（x+m）2=n的形式，则m、n的值是（        ）
    A、  3，8 B、  3，10 C、  -3，3 D、  -3，10

    查看试题解析

  • 5. 在▱ABCD中，已知∠A：∠B=1：5，则∠D的度数是（ ）
    A、 15° B、 30° C、  150° D、  165°

    查看试题解析

  • 6. 学史明理，学史增信，学史崇德，学史力行。某校团委组织团员开展“百年党史”知识竞赛，八年级某班6位参赛同学成绩如下表，则以下说法不正确的是（      ）

    参赛同学

    1号

    2号

    3号

    4号

    5号

    6号

    成绩

    84

    88

    81

    84

    89

    84
    A、  6位参赛同学成绩的平均数是85 B、  6位参赛同学成绩的众数是84 C、  6位参赛同学成绩的方差为 223 D、  6位参赛同学成绩的中位数是82.5

    查看试题解析

  • 7. 某模具公司销售员小王一月份销售额为8万元，已知小王第一季度销售额为34.88万元，若设小王平均每月销售额的增长率均为x，可以列出方程为（        ）
    A、  8（1+x）2=34.88 B、 8（1+3x）=34.88 C、 8[1+（1+x）+（1+x）2]= 34.88 D、  34.88（1-x）2=8

    查看试题解析

  • 8. 如图，在菱形ABCD中，AC与BD相交于点O，BC的垂直平分线EF分别交BC，AC于点E、F，连接DF，若∠BCD=70°，则∠ADF的度数是（          ）

           

    A、  60° B、  75° C、  80° D、  110°

    查看试题解析

  • 9. 已知关于x的一元二次方程ax2+bx+c=0，实数a、b、c满足4a-2b+c=0，则下列说法正确的是（        ）
    A、方程有两个实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根的情况无法确定

    查看试题解析

  • 10. 如图，ΔABC中，∠B > ∠C，点D，E分别是边AB，AC的中点，点F是边BC上的动点，连接DE、DF、EF，

    则下列四个判断中不一定正确的是（       ）

    A、  若点F是BC的中点，则EF=DB B、  若EF=DB，则点F是BC的中点 C、  若点F是BC的中点，则EC=DF D、  若EC=DF，则点F是BC的中点

    查看试题解析

二、填空题

  • 11. 计算5+ 9 的结果是

    查看试题解析

  • 12. 一个多边形的外角和是内角和的 25 ，则这个多边形的边数是

    查看试题解析

  • 13. 如图，A、B、C、D均在正方形网格的格点上，则∠ABC-∠DAC=_°

                                                        

    查看试题解析

  • 14. 如图，在矩形ABCD中，边AB，AD的长分别为3和2，点E在CD上，点F在AB的延长线上，且EC=BF，连接FC。

    (1)、当DE=2时，则FC的长是；  
    (2)、点E在边CD上移动的过程中，AE+FC的最小值是

    查看试题解析

三、综合题

  • 15. 计算： (3)2+2(2−1)−40÷5

    查看试题解析

  • 16. 解方程：x（x-2）=3.

    查看试题解析

  • 17. 如图，将一张长为8cm，宽为5cm的矩形纸片ABCD（AD>AB）剪去了一角，量得DF=2cm，BE=4cm，求EF的长。

    查看试题解析

  • 18. 如图所示的正方形网格中，每个小正方形的边长都是1个单位长度，线段AB的端点A，B都在正方形网格的格点上.

    (1)、请在下面的网格中画出平行四边形ABCD，使AD= 13 （点C，D都在正方形网格的格点上，画出一个正确的图形即可）；
    (2)、在（1）中所画出的平行四边形ABCD的对角线BD的长是。

    查看试题解析

  • 19. 如图，在平行四边形ABCD中，点E、F分别在边AD、BC上，且DE=BF，连接EF交AC于点O；

    求证：OE=OF

    查看试题解析

  • 20. 某网店销售某种玩具，平均每天可售出30件，每件盈利50元。为了扩大销售，增加盈利，该网店采取了降价措施，在每件盈利不少于32元的前提下，销售一段时间后，发现销售单价每降低1元，平均每天可多售出2件，若每件商品降价a（a为正数）元。
    (1)、用含a的代数式表示出平均每天销售的数量，并直接写出a的取值范围；
    (2)、若该网店每天销售利润为2100元时，求a的值.

    查看试题解析

  • 21. 如图，在四边形ABCD中，AD//BC，对角线AC⊥BD，垂足为E，点F是BC延长线上的点，且DF⊥DB。

    (1)、求证：AD=CF；
    (2)、当点C为BF中点时，求证：四边形ABCD是菱形；
    (3)、在（2）的条件下，当△BDF满足什么条件时，四边形ABCD是正方形？（不必说明理由）

    查看试题解析

  • 22. 为了解某校学生课外阅读情况，随机调查了部分学生在一周内借阅图书的次数，根据调查结果绘制了扇形统计图和条形统计图，部分信息如下：

                                 

    请你根据统计图中的信息，解答下列问题.

    (1)、图1中a= ， 并补全图2中的条形统计图；
    (2)、求抽取的这部分学生一周内平均每人阅读的次数；
    (3)、根据本次调查的结果，估计该校3000名学生在一周内借阅图书为 “3次及3次以上”的人数；

    查看试题解析

  • 23. 在正方形ABCD中，点E，F，G分别在边AD，AB，CD上（点E、F、G不与正方形的顶点重合），BE，FG相交于点O，且FG⊥BE.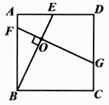

    (1)、猜想BE与FG的数量关系并证明；
    (2)、证明：DG=AF+AE；
    (3)、若AE= 3 ，FG=4，请直接写出点C到直线BE的距离；

    查看试题解析