初中数学暑假作业(人教版:八年级升九年级):02第十七章勾股定理复习题
试卷更新日期:2021-07-02 类型:复习试卷
一、单选题
-
1. 在下列由线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )A、a=4,b=5,c=6 B、a=12,b=5,c=13 C、a=6,b=8,c=10 D、a=7,b=24,c=252. 三个正方形的面积如图所示,则S的值为( )
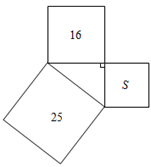 A、3 B、4 C、9 D、123. 在△ABC中,∠A,∠B,∠C的对边分别是a、b、c,下列说法错误的是( )A、如果∠C-∠B=∠A,则△ABC是直角三角形 B、如果c2=b2-a2 , 则△ABC是直角三角形 C、如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 D、如果a2+b2≠c2 , 则△ABC不是直角三角形4. 下列各组数是勾股数的是( )A、0.3,0.4,0.5 B、7,8,9 C、6,8,10 D、 , ,5. 等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为( )A、 B、 C、 或 D、4或6. 如图,有两棵树分别用线段AB和CD表示,树高AB=15米,CD=7米,两树间的距离BD=6米,一只鸟从一棵树的树梢(点A)飞到另一棵树的树梢(点C),则这只鸟飞行的最短距离AC=( )
A、3 B、4 C、9 D、123. 在△ABC中,∠A,∠B,∠C的对边分别是a、b、c,下列说法错误的是( )A、如果∠C-∠B=∠A,则△ABC是直角三角形 B、如果c2=b2-a2 , 则△ABC是直角三角形 C、如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 D、如果a2+b2≠c2 , 则△ABC不是直角三角形4. 下列各组数是勾股数的是( )A、0.3,0.4,0.5 B、7,8,9 C、6,8,10 D、 , ,5. 等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为( )A、 B、 C、 或 D、4或6. 如图,有两棵树分别用线段AB和CD表示,树高AB=15米,CD=7米,两树间的距离BD=6米,一只鸟从一棵树的树梢(点A)飞到另一棵树的树梢(点C),则这只鸟飞行的最短距离AC=( ) A、6米 B、8米 C、10米 D、12米7. 如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A、6米 B、8米 C、10米 D、12米7. 如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( ) A、29 B、32 C、36 D、458. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )
A、29 B、32 C、36 D、458. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )
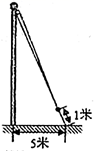 A、12 B、13 C、15 D、249. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,大正方形面积为64,小正方形面积为9,若用x,y表示直角三角形的两直角边长(x>y),请观察图案,下列关系式中不正确的是( )
A、12 B、13 C、15 D、249. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,大正方形面积为64,小正方形面积为9,若用x,y表示直角三角形的两直角边长(x>y),请观察图案,下列关系式中不正确的是( ) A、x2+y2=64 B、x-y=3 C、2xy+9=64 D、x+y=1110. 将一根 的细木棍放入长,宽,高分别为 , , 的长方体盒子中,则细木棍露在外面的最短长度为( ).
A、x2+y2=64 B、x-y=3 C、2xy+9=64 D、x+y=1110. 将一根 的细木棍放入长,宽,高分别为 , , 的长方体盒子中,则细木棍露在外面的最短长度为( ).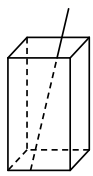 A、8 B、7 C、6 D、5
A、8 B、7 C、6 D、5二、填空题
-
11. 如图所示,一棵9m高的树被风刮断了,树顶落在离树根6m处,则折断处的高度AB为.
 12. 如图是放在地面上的一个长方体盒子,其中AB=24cm,BC=12cm,BF=7cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为.
12. 如图是放在地面上的一个长方体盒子,其中AB=24cm,BC=12cm,BF=7cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为. 13. 如图,在 中, ,点 在 上,且 ,若 ,则 .
13. 如图,在 中, ,点 在 上,且 ,若 ,则 .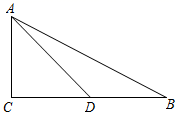 14. 若一直角三角形的两边长为4、5,则第三边长的平方为15. 如图,在一个高为5m , 长为13m的楼梯表面铺地毯,则地毯的长度至少是 .
14. 若一直角三角形的两边长为4、5,则第三边长的平方为15. 如图,在一个高为5m , 长为13m的楼梯表面铺地毯,则地毯的长度至少是 . 16. 如图,每个小正方形的边长都为1,则 的周长为
16. 如图,每个小正方形的边长都为1,则 的周长为 17. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的, , ,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长(图中实线部分)是 .
17. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的, , ,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长(图中实线部分)是 . 18. 如图,四边形 中, 于 , , , ,则 的长为 .
18. 如图,四边形 中, 于 , , , ,则 的长为 .
三、计算题
-
19.
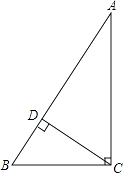
已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
 20. 如图,一高层住宅发生火灾,消防车立即赶到距大厦8米处(车尼AE到大厦墙面CD),升起云梯到火灾窗口B,已知云梯AB长17米,云梯底部距地面的高AE=1.5米;问发生火灾的住户窗口距离地面多高?
20. 如图,一高层住宅发生火灾,消防车立即赶到距大厦8米处(车尼AE到大厦墙面CD),升起云梯到火灾窗口B,已知云梯AB长17米,云梯底部距地面的高AE=1.5米;问发生火灾的住户窗口距离地面多高? 21. 如图,一根2.5米长的竹竿AB斜靠在竖直的墙AC上,这时B到墙底端为0.7米,如果竹竿的底端沿地面向外滑动0.8米,那么点A将向下移动多少米?
21. 如图,一根2.5米长的竹竿AB斜靠在竖直的墙AC上,这时B到墙底端为0.7米,如果竹竿的底端沿地面向外滑动0.8米,那么点A将向下移动多少米?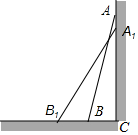 22. 如已知:如图,四边形 中 , , ,且 .试求 的度数.
22. 如已知:如图,四边形 中 , , ,且 .试求 的度数. 23. 如图在 中, ,点E,F分别在 上,求证: .
23. 如图在 中, ,点E,F分别在 上,求证: . 24. 如图,在 中, ,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 同时出发,问过 时, 的面积为多少?
24. 如图,在 中, ,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 同时出发,问过 时, 的面积为多少? 25. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
25. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒. (1)、出发2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为直角三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
(1)、出发2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为直角三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?