初中数学暑假作业(人教版:八年级升九年级):04第十九章一次函数复习题
试卷更新日期:2021-07-02 类型:复习试卷
一、单选题
-
1. 若一次函数y=(2m+1)x+m﹣3的图象不经过第二象限,则m的取值范围是( )A、m B、m<3 C、 m≤3 D、 m<32. 已知在一次函数y=﹣3x+2的图象上有三个点A(﹣3,y1),B(3,y2),C(﹣4,y3),则下列各式中正确的是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y3<y2<y13. 函数y= 中,自变量x的取值范围是( )A、x>4 B、x≥2 C、x≥2且x≠4 D、x≠44. 已知一次函数y=2x﹣1经过P(a , b),则2b﹣4a的值为( )A、1 B、﹣2 C、2 D、﹣15. 若一个等腰三角形的顶角度数为y(度),底角度数为x(度),则它们的函数表达式应是( )A、y=180﹣2x(0<x<90) B、y=90﹣x C、y=180﹣ x(0<x<90) D、y=90+x6. 在平面直角坐标系中,已知函数 的图象,则该函数的图象可能是( )A、
 B、
B、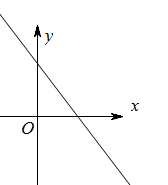 C、
C、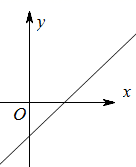 D、
D、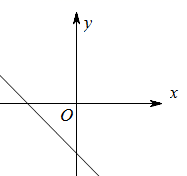 7. 若一次函数 的图象经过点 ,且函数值 随着 增大而减小,则点 的坐标可能为( )A、 B、 C、 D、8. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(时)之间的函数图象如图所示,则下列说法:①客车比出租车晚4小时到达目的地;②两车出发后3.75小时相遇;③两车相遇时客车距乙地还有225千米;④客车的速度为60千米/时,出租车的速度为100千米/时,其中正确的有( )
7. 若一次函数 的图象经过点 ,且函数值 随着 增大而减小,则点 的坐标可能为( )A、 B、 C、 D、8. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(时)之间的函数图象如图所示,则下列说法:①客车比出租车晚4小时到达目的地;②两车出发后3.75小时相遇;③两车相遇时客车距乙地还有225千米;④客车的速度为60千米/时,出租车的速度为100千米/时,其中正确的有( ) A、1个 B、2个 C、3个 D、4个9. 当k取不同的值时,y关于x的函数y=kx+2(k≠0)的图象为总是经过点(0,2)的直线,我们把所有这样的直线合起来,称为经过点(0,2)的“直线束”.那么,下面经过点(﹣1,2)的直线束的函数式是( )
A、1个 B、2个 C、3个 D、4个9. 当k取不同的值时,y关于x的函数y=kx+2(k≠0)的图象为总是经过点(0,2)的直线,我们把所有这样的直线合起来,称为经过点(0,2)的“直线束”.那么,下面经过点(﹣1,2)的直线束的函数式是( )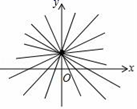 A、y=kx﹣2(k≠0) B、y=kx+k+2(k≠0) C、y=kx﹣k+2(k≠0) D、y=kx+k﹣2(k≠0)10. 如图,在平面直角坐标系中,线段AB的端点坐标为A(-3,-5),B(2,-3),若直线y=kx+1与线段AB有交点,则k的值不可能是( )
A、y=kx﹣2(k≠0) B、y=kx+k+2(k≠0) C、y=kx﹣k+2(k≠0) D、y=kx+k﹣2(k≠0)10. 如图,在平面直角坐标系中,线段AB的端点坐标为A(-3,-5),B(2,-3),若直线y=kx+1与线段AB有交点,则k的值不可能是( ) A、-5 B、-1 C、3 D、5
A、-5 B、-1 C、3 D、5二、填空题
-
11. 如图,直线l1的解析式是y=2x-1,直线l2的解析式是y=x+1,则方程组 的解是 .
 12. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是 .
12. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是 .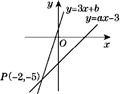 13. 将函数 的图象平移,使它经过点 ,则平移后的函数表达式是.14. 已知 是一次函数,则 .15. 如图所示,在平面直角坐标系中,点P(x,y)是直线y = - x + 6上第一象限的点,点A的坐标是(4,0),O是坐标原点,△PAO的面积为S,则S关于x的函数表达式为 .
13. 将函数 的图象平移,使它经过点 ,则平移后的函数表达式是.14. 已知 是一次函数,则 .15. 如图所示,在平面直角坐标系中,点P(x,y)是直线y = - x + 6上第一象限的点,点A的坐标是(4,0),O是坐标原点,△PAO的面积为S,则S关于x的函数表达式为 .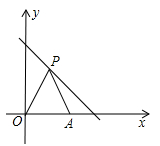 16. 在平面直角坐标系中,一次函数 的图象经过 两点,若 ,则 .(填“>”“<”或“=”)17. 已知直线 经过第一,二,四象限,那么直线 不经过第象限.18. 一次函数y=kx+b(k、b是常数)当自变量x的取值为1≤x≤5时,对应的函数值的范围为﹣2≤y≤2,则此一次函数的解析式为.
16. 在平面直角坐标系中,一次函数 的图象经过 两点,若 ,则 .(填“>”“<”或“=”)17. 已知直线 经过第一,二,四象限,那么直线 不经过第象限.18. 一次函数y=kx+b(k、b是常数)当自变量x的取值为1≤x≤5时,对应的函数值的范围为﹣2≤y≤2,则此一次函数的解析式为.三、解答题
-
19. 已知直线 经过点 、 两点,求这条直线的表达式.20. 已知 , 与 成反比例, 与 成正比例,并且当 时, ;当 时, .求:y关于x的函数解析式.21. 在给出的网格中画出一次函数 的图象,并结合图象求:

①方程 的解;
②不等式 的解集;
③不等式 的解集.
22. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.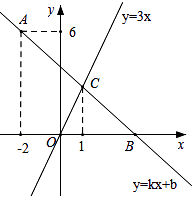 (1)、求k、b的值;(2)、若点D在y轴负半轴上,且满足S△COD= S△BOC , 求点D的坐标.23. 已知一次函数y=(1﹣2m)x+m+1及坐标平面内一点P(2,0);(1)、若一次函数图象经过点P(2,0),求m的值;(2)、若一次函数的图象经过第一、二、三象限;
(1)、求k、b的值;(2)、若点D在y轴负半轴上,且满足S△COD= S△BOC , 求点D的坐标.23. 已知一次函数y=(1﹣2m)x+m+1及坐标平面内一点P(2,0);(1)、若一次函数图象经过点P(2,0),求m的值;(2)、若一次函数的图象经过第一、二、三象限;①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,则y1y2(填“>”、”=”、”<”).
24. 如图4, 、 分别表示 步行与 骑车在同一路上行驶的路程 与时间 的关系. 图4(1)、 出发时与 相距千米;(2)、走了一段路后,自行车发生故障,进行修理,所用的时间是小时;(3)、 出发后小时与 相遇;(4)、若 的自行车不发生故障,保持出发时的速度前进,小时与 相遇,相遇点离 的出发点千米,在图中表示出这个相遇点 ;(5)、求出 行走的路程 与时间 的函数关系式.25. 某办公用品销售商店推出两种优惠方法:①购买1个书包,赠送1支水性笔;②购买书包和水性笔一律按 9 折优惠:书包每个定价 20 元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).设购买费用为y元,购买水性笔x支.(1)、分别写出两种优惠方法下支付的费用 y(元)与所买水性笔支数 x(支)之间的函数关系式;(2)、通过对 x的取值情况进行分析,说明按哪种优惠方法购买更便宜;(3)、小丽和同学需买书包4个和水性笔12支,请你设计怎样购买更合算.
图4(1)、 出发时与 相距千米;(2)、走了一段路后,自行车发生故障,进行修理,所用的时间是小时;(3)、 出发后小时与 相遇;(4)、若 的自行车不发生故障,保持出发时的速度前进,小时与 相遇,相遇点离 的出发点千米,在图中表示出这个相遇点 ;(5)、求出 行走的路程 与时间 的函数关系式.25. 某办公用品销售商店推出两种优惠方法:①购买1个书包,赠送1支水性笔;②购买书包和水性笔一律按 9 折优惠:书包每个定价 20 元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).设购买费用为y元,购买水性笔x支.(1)、分别写出两种优惠方法下支付的费用 y(元)与所买水性笔支数 x(支)之间的函数关系式;(2)、通过对 x的取值情况进行分析,说明按哪种优惠方法购买更便宜;(3)、小丽和同学需买书包4个和水性笔12支,请你设计怎样购买更合算.