初中数学浙教版八年级上册1.3 证明 同步练习
试卷更新日期:2021-07-02 类型:同步测试
一、单选题
-
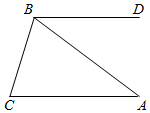
1. 如图,BD平分∠ABC,若∠1=∠2,则( )
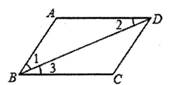 A、AB∥CD B、AD∥BC C、AD=BC D、AB=CD2. 如图,点D、E分别在线段 、 上,连接 、 .若 , , ,则 的大小为( )
A、AB∥CD B、AD∥BC C、AD=BC D、AB=CD2. 如图,点D、E分别在线段 、 上,连接 、 .若 , , ,则 的大小为( )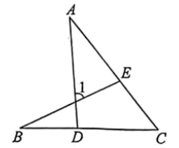 A、60° B、70° C、75° D、85°3. 小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )
A、60° B、70° C、75° D、85°3. 小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )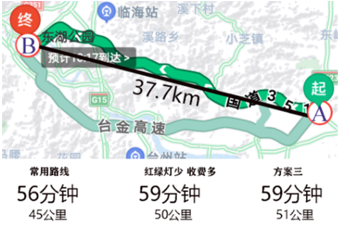 A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线4. 如图,设点P是直线 外一点,PQ⊥ ,垂足为点Q,点T是直线 上的一个动点,连结PT,则( )
A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线4. 如图,设点P是直线 外一点,PQ⊥ ,垂足为点Q,点T是直线 上的一个动点,连结PT,则( )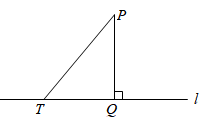 A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ5. 某同学的作业如下框,其中※处填的依据是( )
A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ5. 某同学的作业如下框,其中※处填的依据是( )如图,已知直线 .若 ,则 .
请完成下面的说理过程.
解:已知 ,
根据(内错角相等,两直线平行),得 .
再根据( ※ ),得 .
 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补6. 如图,直线 的顶点 在 上,若 ,则 ( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补6. 如图,直线 的顶点 在 上,若 ,则 ( )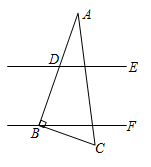 A、 B、 C、 D、7. 如图,将矩形纸片 沿 折叠后,点D、C分别落在点 、 的位置, 的延长线交 于点G,若 ,则 等于( )
A、 B、 C、 D、7. 如图,将矩形纸片 沿 折叠后,点D、C分别落在点 、 的位置, 的延长线交 于点G,若 ,则 等于( )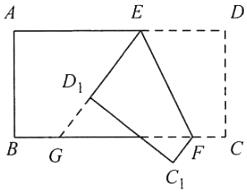 A、 B、 C、 D、8. 如图,现将一块三角板含有 角的顶点放在直尺的一边上,若 ,那么 的度数为( )
A、 B、 C、 D、8. 如图,现将一块三角板含有 角的顶点放在直尺的一边上,若 ,那么 的度数为( )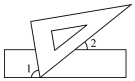 A、 B、 C、 D、9. 如图,点E在射线AB上,要AD BC,只需( )
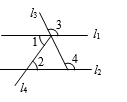
A、 B、 C、 D、9. 如图,点E在射线AB上,要AD BC,只需( ) A、∠A=∠CBE B、∠A=∠C C、∠C=∠CBE D、∠A+∠D= 180°10. 如图,∠1=80°,∠2=80°,∠5=70°,则∠3的大小是( )
A、∠A=∠CBE B、∠A=∠C C、∠C=∠CBE D、∠A+∠D= 180°10. 如图,∠1=80°,∠2=80°,∠5=70°,则∠3的大小是( ) A、70° B、80° C、100° D、110°11. 如图,AB∥CD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为( )
A、70° B、80° C、100° D、110°11. 如图,AB∥CD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为( ) A、18° B、32° C、50° D、60°12. 如图,能判定DE∥BC的条件是( )
A、18° B、32° C、50° D、60°12. 如图,能判定DE∥BC的条件是( ) A、∠ABC+∠BAE=180 B、∠C=∠BAC C、∠C+∠BAD=180 D、∠C=∠BAD13. 如图,直线 ,直线c与直线a,b分别交于A,B两点, 于点A,交直线b于点C,如果 ,那么 的度数为( )
A、∠ABC+∠BAE=180 B、∠C=∠BAC C、∠C+∠BAD=180 D、∠C=∠BAD13. 如图,直线 ,直线c与直线a,b分别交于A,B两点, 于点A,交直线b于点C,如果 ,那么 的度数为( ) A、 B、 C、 D、14. 将一副三角板按如图所示的方式摆放,则∠1=( )
A、 B、 C、 D、14. 将一副三角板按如图所示的方式摆放,则∠1=( )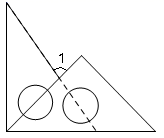 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 如图, ,那么 的度数为 .
 16. 如图,梯子的各条横档互相平行,若 ,则 .
16. 如图,梯子的各条横档互相平行,若 ,则 . 17. 如图,AB CD ,若∠B+∠D+∠BED=180°,则∠BED=.
17. 如图,AB CD ,若∠B+∠D+∠BED=180°,则∠BED=. 18. 将一把直尺和一块直角三角板如图放置,如果∠α=43°,则∠β的度数是度.
18. 将一把直尺和一块直角三角板如图放置,如果∠α=43°,则∠β的度数是度. 19. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为 .
19. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为 . 20. 一副三角板按如图所示放置,AB∥DC , 则∠ACE的度数为°.
20. 一副三角板按如图所示放置,AB∥DC , 则∠ACE的度数为°. 21. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射,如果被b反射出的光线n与光线m平行,且 ,那么 的度数为 .
21. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射,如果被b反射出的光线n与光线m平行,且 ,那么 的度数为 . 22. 如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
22. 如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 . 23. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .
23. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .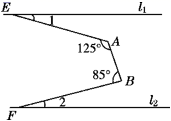
三、计算题
-
24. 如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连接OF.
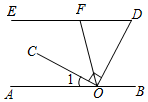 (1)、求证:ED∥AB.(2)、若OF平分∠COD,∠OFD=70°,求∠1的度数.25. 在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F.
(1)、求证:ED∥AB.(2)、若OF平分∠COD,∠OFD=70°,求∠1的度数.25. 在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F. (1)、如图,当点E在线段CD上时,求证:∠DEF=∠DCB.(2)、若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .
(1)、如图,当点E在线段CD上时,求证:∠DEF=∠DCB.(2)、若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .四、解答题
-
26. 如图,EF//AD,∠1=∠2,∠BAC=82°,请将求∠AGD的过程填写完整.
解:因为EF//AD
所以∠2=∠ ▲ ( )
又因为∠1=∠2
所以∠1=∠3( )
所以AB// ▲ ( )
所以∠BAC+∠ ▲ =180°( )
因为∠BAC=82°
所以∠AGD= ▲ °
 27. 如图,已知 AB∥ CD , ∠1 = ∠2,试说明: ∠E =∠F.
27. 如图,已知 AB∥ CD , ∠1 = ∠2,试说明: ∠E =∠F. 28. 如图,四边形 中, ,点 在 边上, 于点 , ,求证: .
28. 如图,四边形 中, ,点 在 边上, 于点 , ,求证: .
五、综合题
-
29. 问题情境
 (1)、如图1,已知 ,求 的度数.佩佩同学的思路:过点 作 ,进而 ,由平行线的性质来求 ,求得 ;(2)、问题迁移
(1)、如图1,已知 ,求 的度数.佩佩同学的思路:过点 作 ,进而 ,由平行线的性质来求 ,求得 ;(2)、问题迁移图2,图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合 与 相交于点 ,有一动点 在边 上运动,连接 ,记 .
①如图2,当点 在 两点之间运动时,请直接写出 与 之间的数量关系;
②如图3,当点 在 两点之间运动时, 与 之间有何数量关系?请判断并说明理由.
30. 已知:三角形ABC和三角形DEF位于直线MN的两侧中,直线MN经过点C , 且 ,其中 , , ,点E、F均落在直线MN上. (1)、如图1,当点C与点E重合时,求证: ;聪明的小丽过点C作 ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.(2)、将三角形DEF沿着NM的方向平移,如图2,求证: ;(3)、将三角形DEF沿着NM的方向平移,使得点E移动到点 ,画出平移后的三角形DEF , 并回答问题,若 ,则 . (用含 的代数式表示)
(1)、如图1,当点C与点E重合时,求证: ;聪明的小丽过点C作 ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.(2)、将三角形DEF沿着NM的方向平移,如图2,求证: ;(3)、将三角形DEF沿着NM的方向平移,使得点E移动到点 ,画出平移后的三角形DEF , 并回答问题,若 ,则 . (用含 的代数式表示)