2021-2022学年人教版九年级上册第二十三章 旋转单元测试
试卷更新日期:2021-07-02 类型:单元试卷
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个2. 利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点 为旋转中心,顺时针(或逆时针)旋转角度 ,依次旋转五次而组成,则旋转角 的值不可能是( )
A、4个 B、3个 C、2个 D、1个2. 利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点 为旋转中心,顺时针(或逆时针)旋转角度 ,依次旋转五次而组成,则旋转角 的值不可能是( ) A、36° B、72° C、144° D、216°3. 若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是( )A、1 B、3 C、5 D、74. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )
A、36° B、72° C、144° D、216°3. 若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是( )A、1 B、3 C、5 D、74. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )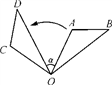 A、50° B、60° C、40° D、30°5. 始于唐代的青花瓷给人以古朴、典雅之美.关于如图所示的青花瓷图案,下列说法正确的是( )
A、50° B、60° C、40° D、30°5. 始于唐代的青花瓷给人以古朴、典雅之美.关于如图所示的青花瓷图案,下列说法正确的是( ) A、它是中心对称图形,但不是轴对称图形 B、它是轴对称图形,但不是中心对称图形 C、它既是中心对称图形,又是轴对称图形 D、它既不是中心对称图形,又不是轴对称图形6. 如图, 方格纸上的两条对称轴 、 相交于中心点 ,对△ABC分别作下列变换:
A、它是中心对称图形,但不是轴对称图形 B、它是轴对称图形,但不是中心对称图形 C、它既是中心对称图形,又是轴对称图形 D、它既不是中心对称图形,又不是轴对称图形6. 如图, 方格纸上的两条对称轴 、 相交于中心点 ,对△ABC分别作下列变换:①先以点 为中心顺时针方向旋转 ,再向右平移 格、向上平移 格;②先以点 为中心作中心对称图形,再以点 的对应点为中心逆时针方向旋转 ;③先以直线 为轴作轴对称图形,再向上平移 格,再以点 的对应点为中心顺时针方向旋转 .其中,能将△ABC变换成△PQR的是( )
 A、①② B、①③ C、②③ D、①②③7. 已知点(a,a),给出下列变换:
A、①② B、①③ C、②③ D、①②③7. 已知点(a,a),给出下列变换:①关于x轴的轴对称变换; ②关于直线y=﹣x的轴对称变换; ③关于原点的中心对称变换;④绕原点旋转180°. 其中通过变换能得到像的坐标为(﹣a,﹣a)的变换是( )
A、①②④ B、②③④ C、③④ D、②③8. 在平面直角坐标系中,已知点P(x0 , ﹣y0),连接OP,将线段OP绕点O顺时针旋转90°后,得到线段OQ,则点Q的坐标是( )A、(﹣y0 , ﹣x0) B、(﹣y0 , x0) C、(y0 , x0) D、(﹣x0 , y0)9. 如图,已知正方形ABCD的边长为3,E为CD上一点,DE=1,以点A为中心,把△ADE顺时针旋转90°得△ABE',连接EE',则EE'的长度为( ) A、 B、4 C、3 D、10. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2020次得到正方形OA2020B2020C2020 , 如果点A的坐标为(1,0),那么点B2020的坐标为( )
A、 B、4 C、3 D、10. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2020次得到正方形OA2020B2020C2020 , 如果点A的坐标为(1,0),那么点B2020的坐标为( )
 A、(﹣1,1) B、(- ,0) C、(﹣1,﹣1) D、(0,- )
A、(﹣1,1) B、(- ,0) C、(﹣1,﹣1) D、(0,- )二、填空题
-
11. 在 ①平行四边形、 ②正方形、 ③等边三角形、 ④等腰梯形、 ⑤菱形、 ⑥圆、⑦正八边形这些图形中,既是轴对称图形又是中心对称图形的是(填序号)12. 若点(a+1,3)与点(-2,b-2)关于y轴对称,则点P(-a,b)关于原点对称的点的坐标为13. 如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE.若AB=2,∠ACB=30°,则线段CD的长度为.
 14. 如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是 .
14. 如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是 . 15. 如图,△ABC中,∠ACB=90°,∠ABC=32°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为 .
15. 如图,△ABC中,∠ACB=90°,∠ABC=32°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为 .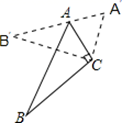 16. 如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于°.
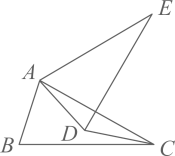
16. 如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于°.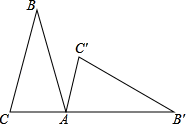 17. 如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为 .
17. 如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为 .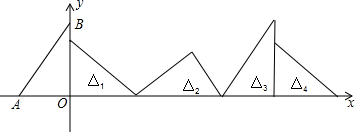 18. 如图,四边形ABCD为长方形, 旋转后能与 重合,旋转中心是点 ;旋转了多少度 ;连结FC,则 是 三角形.
18. 如图,四边形ABCD为长方形, 旋转后能与 重合,旋转中心是点 ;旋转了多少度 ;连结FC,则 是 三角形.
三、解答题
-
19. 已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。20. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,1),B(-1,3),C(0,1).

( 1 )将△ABC以点C为旋转中心旋转180°,画出旋转后的△A1B1C;
( 2 )平移△ABC,若点A的对应点A2的坐标为(-5,-3),画出平移后的△A2B2C2;
( 3 )若△A2B2C2和△A1B1C关于点P中心对称,请直接写出旋转中心P的坐标.
21. 如图所示,网格中每个小正方形的边长为1,请你认真观察图(1)中的三个网格中阴影部分构成的图案,解答下列问题: (1)、这三个图案都具有以下共同特征:都是对称图形,都不是对称图形.(2)、请在图(2)中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图(1)中所给出的图案相同.
(1)、这三个图案都具有以下共同特征:都是对称图形,都不是对称图形.(2)、请在图(2)中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图(1)中所给出的图案相同. 22. 如图,若在正方形 中,点 为 边上一点,点 为 延长线上一点,且 ,则 与 之间有怎样的数量关系和位置关系?请说明理由.
22. 如图,若在正方形 中,点 为 边上一点,点 为 延长线上一点,且 ,则 与 之间有怎样的数量关系和位置关系?请说明理由.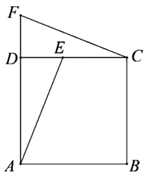 23. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
23. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2). (1)、在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(1)、在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)、把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2 , 点C2在AB上.①旋转角为多少度?
②写出点B2的坐标.