初中数学浙教版八年级上册1.4 全等三角形 同步练习
试卷更新日期：2021-07-02 类型：同步测试
一、单选题
-
1. 如图，已知 ≌ ，若 ， ，则 的长为（ ）.
A、5 B、6 C、7 D、82. 下列各组中的两个图形属于全等图形的是（ ）A、
B、
C、
D、
3. 如图，两个三角形全等，则 等于（ ）
A、 B、 C、 D、4. 如图，△ACB≌△A′C B′，∠ACB＝70°，∠ACB′＝100°，则∠BCA′度数是（ ）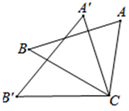
A、40° B、35 C、30° D、45°5. 如图， ，若 ， ，则 的度数为（ ）
A、80° B、35° C、70° D、30°6. 如图，点B，E，C，F在一条直线上， ，则下列结论正确的是（ ）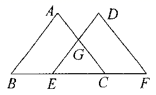
A、 B、 C、 D、7. 如图，若△ABC≌△DEF，BE＝22，BF＝5，则FC的长度是（ ）
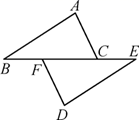A、10 B、12 C、8 D、168. 下列说法正确的是（ ）A、两个长方形是全等图形 B、形状相同的两个三角形全等 C、两个全等图形面积一定相等 D、所有的等边三角形都是全等三角形9. 如图，两个三角形全等，其中已知某些边的长度和某些角的度数，则x的度数是（ ）
A、 B、 C、 D、10. 如图，若△OAD≌△OBC，且∠O=65°， ∠C=20°，求∠OAD的度数（ ）
A、20° B、65° C、80° D、95°11. 如图，△ABC △DEF，点E，C，F，B在同一条直线上．下列结论正确的是（ ）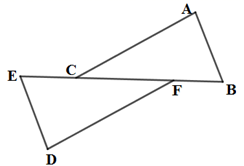
A、 B、 C、 D、12. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ，大正方形边长为 ，则一个直角三角形的面积等于（ ）
A、 B、 C、 D、13. 如图， ， ， ， ， ，CE的长为（ ）
A、1 B、2 C、3 D、414. 如图，已知△ABC与△BDE全等，其中点D在边AB上，AB＞BC，BD=CA，DE∥AC，BC与DE交于点F，下列与AD+AC相等的是（ ）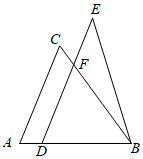
A、DE B、BE C、BF D、DF15. 如图，△ABC≌△CDA，∠BAC＝∠DCA，则BC 的对应边是 （ ）
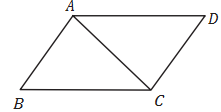A、CD B、CA C、DA D、AB二、填空题
-
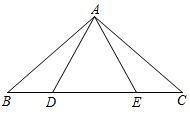
16. 如图，点 、 、 、 在一条直线上，若 ， ， ，则 的长为.
17. 一个三角形的三条边长分别为 ， ，x，另一个三角形的三条边长分别为y， ， ，若这两个三角形全等，则 .18. 如图，已知△ABC≌△DEF，则DE=.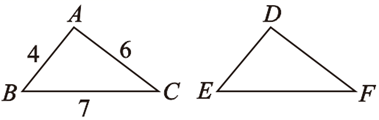
19. 如图， ，其中 ， ，则 °.
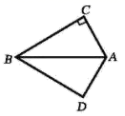20. 如图：若△ABE≌△ACF，且AB=5，AE=2，则EC的长为
21. 如图，△ABC≌△DBE，△ABC的周长为30，AB=9，BE=8，则AC的长是
22. 已知 ≌ ， 的周长为100， ， ，则 .23. 如图，△ABC≌△ADE，且点D在BC上，∠BAE＝114°，∠BAD＝40°，则∠E的度数是 ．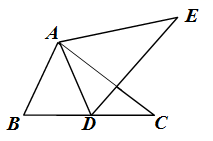
24. 如图， ， ， ，则 ．
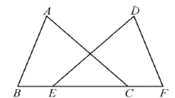25. 已知△ABC≌△DEF，△ABC的三边分别为3，m，n，△DEF的三边分别为5，p，q.若△ABC的三边均为整数，则m+n+p+q的最大值为.三、解答题
