山东省济宁市2021年中考数学试卷
试卷更新日期:2021-07-01 类型:中考真卷
一、单选题
-
1. 若盈余2万元记作 万元,则 万元表示( )A、盈余2万元 B、亏损2万元 C、亏损 万元 D、不盈余也不亏损2. 一个圆柱体如图所示,下面关于它的左视图的说法,其中正确的是( )
 A、既是轴对称图形,又是中心对称图形 B、既不是轴对称图形,又不是中心对称图形 C、是轴对称图形,但不是中心对称图形 D、是中心对称图形,但不是轴对称图形3. 下列各式中,正确的是( )A、 B、 C、 D、4. 如图, , ,若 ,那么 的度数是( )
A、既是轴对称图形,又是中心对称图形 B、既不是轴对称图形,又不是中心对称图形 C、是轴对称图形,但不是中心对称图形 D、是中心对称图形,但不是轴对称图形3. 下列各式中,正确的是( )A、 B、 C、 D、4. 如图, , ,若 ,那么 的度数是( )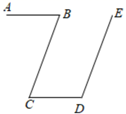 A、 B、 C、 D、5. 计算 的结果是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 计算 的结果是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、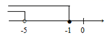 B、
B、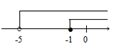 C、
C、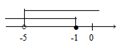 D、
D、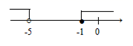 7. 如图,正五边形 中, 的度数为( )
7. 如图,正五边形 中, 的度数为( ) A、 B、 C、 D、8. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20229. 如图,已知 .
A、 B、 C、 D、8. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20229. 如图,已知 .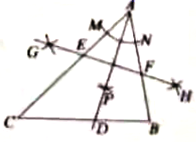
⑴以点A为圆心,以适当长为半径画弧,交 于点M , 交 于点N .
⑵分别以M , N为圆心,以大于 的长为半径画弧,两弧在 的内部相交于点P .
⑶作射线 交 于点D .
⑷分别以A , D为圆心,以大于 的长为半径画弧,两弧相交于G , H两点.
⑸作直线 ,交 , 分别于点E , F .
依据以上作图,若 , , ,则 的长是( )
A、 B、1 C、 D、410. 按规律排列的一组数据: , ,□, , , ,…,其中□内应填的数是( )A、 B、 C、 D、二、填空题
-
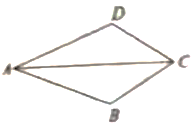
11. 数字5100000用科学记数法表示是 .12. 如图,四边形 中, ,请补充一个条件 , 使 .
 13. 已知一组数据0,1,x,3,6的平均数是y,则y关于x的函数解析式是 .14. 如图, 中, , , ,点O为 的中点,以O为圆心,以 为半径作半圆,交 于点D , 则图中阴影部分的面积是 .
13. 已知一组数据0,1,x,3,6的平均数是y,则y关于x的函数解析式是 .14. 如图, 中, , , ,点O为 的中点,以O为圆心,以 为半径作半圆,交 于点D , 则图中阴影部分的面积是 .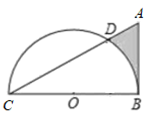 15. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论:
15. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论: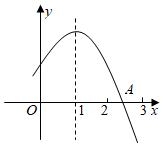
① ;
② ;
③ ;
④方程 必有一个根大于 且小于0.
其中正确的是(只填序号).
三、解答题
-
16. 计算: .17. 某校为了解九年级学生体质健康情况,随机抽取了部分学生进行体能测试,根据测试结果绘制了不完整的条形统计图和扇形统计图,请回答下列问题:
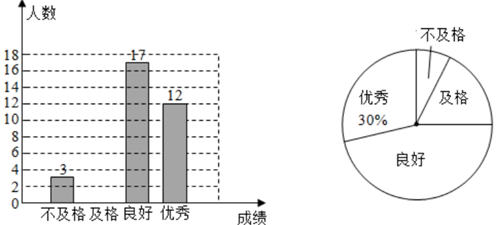 (1)、在这次调查中,“优秀”所在扇形的圆心角的度数是;(2)、请补全条形统计图;(3)、若该校九年级共有学生1200人,则估计该校“良好”的人数是;(4)、已知“不合格”的3名学生中有2名男生、1名女生,如果从中随机抽取两名同学进行体能加试,请用列表法或画树状图的方法,求抽到两名男生的概率多少?18. 如图, 中, , ,点 ,点 ,反比例函数 的图象经过点A .
(1)、在这次调查中,“优秀”所在扇形的圆心角的度数是;(2)、请补全条形统计图;(3)、若该校九年级共有学生1200人,则估计该校“良好”的人数是;(4)、已知“不合格”的3名学生中有2名男生、1名女生,如果从中随机抽取两名同学进行体能加试,请用列表法或画树状图的方法,求抽到两名男生的概率多少?18. 如图, 中, , ,点 ,点 ,反比例函数 的图象经过点A .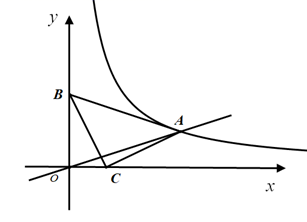 (1)、求反比例函数的解析式;(2)、将直线 向上平移m个单位后经过反比例函数,图象上的点 ,求m,n的值.19. 如图,点C在以 为直径的 上,点D是 的中点,连接 并延长交 于点E , 作 , 交 的延长线于点P .
(1)、求反比例函数的解析式;(2)、将直线 向上平移m个单位后经过反比例函数,图象上的点 ,求m,n的值.19. 如图,点C在以 为直径的 上,点D是 的中点,连接 并延长交 于点E , 作 , 交 的延长线于点P . (1)、求证: 是 的切线;(2)、若 , ,求 的半径.20. 某商场购进甲、乙两种商品共100箱,全部售完后,甲商品共盈利900元,乙商品共盈利400元,甲商品比乙商品每箱多盈利5元.(1)、求甲、乙两种商品每箱各盈利多少元?(2)、甲、乙两种商品全部售完后,该商场又购进一批甲商品,在原每箱盈利不变的前提下,平均每天可卖出100箱.如调整价格,每降价1元,平均每天可以多卖出20箱,那么当降价多少元时,该商场利润最大?最大利润是多少?21. 研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)、求证: 是 的切线;(2)、若 , ,求 的半径.20. 某商场购进甲、乙两种商品共100箱,全部售完后,甲商品共盈利900元,乙商品共盈利400元,甲商品比乙商品每箱多盈利5元.(1)、求甲、乙两种商品每箱各盈利多少元?(2)、甲、乙两种商品全部售完后,该商场又购进一批甲商品,在原每箱盈利不变的前提下,平均每天可卖出100箱.如调整价格,每降价1元,平均每天可以多卖出20箱,那么当降价多少元时,该商场利润最大?最大利润是多少?21. 研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.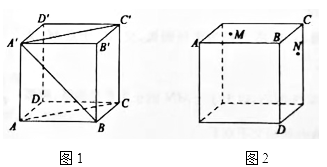 (1)、阅读材料
(1)、阅读材料立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体 (图1).因为在平面 中, , 与 相交于点A , 所以直线 与 所成的 就是既不相交也不平行的两条直线 与 所成的角.
解决问题
如图1,已知正方体 ,求既不相交也不平行的两条直线 与 所成角的大小.
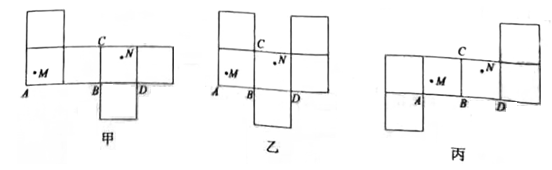
(2)、如图2,M , N是正方体相邻两个面上的点.①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是;
②在所选正确展开图中,若点M到 , 的距离分别是2和5,点N到 , 的距离分别是4和3,P是 上一动点,求 的最小值.
 22. 如图,直线 分别交x轴、y轴于点A , B , 过点A的抛物线 与x轴的另一交点为C , 与y轴交于点 ,抛物线的对称轴l交 于E , 连接 交 于点F .
22. 如图,直线 分别交x轴、y轴于点A , B , 过点A的抛物线 与x轴的另一交点为C , 与y轴交于点 ,抛物线的对称轴l交 于E , 连接 交 于点F .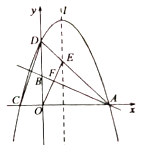 (1)、求抛物线解析式;(2)、求证: ;(3)、P为抛物线上的一动点,直线 交 于点M , 是否存在这样的点P , 使以A , O , M为顶点的三角形与 相似?若存在,求点P的横坐标;若不存在,请说明理由.
(1)、求抛物线解析式;(2)、求证: ;(3)、P为抛物线上的一动点,直线 交 于点M , 是否存在这样的点P , 使以A , O , M为顶点的三角形与 相似?若存在,求点P的横坐标;若不存在,请说明理由.