山东省东营市2021年中考数学试卷
试卷更新日期:2021-07-01 类型:中考真卷
一、单选题
-
1. 16的算术平方根是A、4 B、-4 C、±4 D、82. 下列运算结果正确的是( )A、 B、 C、 D、3. 如图, , 于点F , 若 ,则 ( )
 A、 B、 C、 D、4. 某玩具商店周年店庆,全场八折促销,持会员卡可在促销活动的基础上再打六折.某电动汽车原价300元,小明持会员卡购买这个电动汽车需要花( )元A、240 B、180 C、160 D、1445. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A、 B、 C、 D、4. 某玩具商店周年店庆,全场八折促销,持会员卡可在促销活动的基础上再打六折.某电动汽车原价300元,小明持会员卡购买这个电动汽车需要花( )元A、240 B、180 C、160 D、1445. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )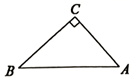 A、 B、 C、 D、6. 经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )A、 B、 C、 D、7. 已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )
A、 B、 C、 D、6. 经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )A、 B、 C、 D、7. 已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )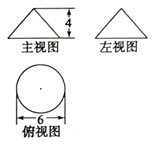 A、214° B、215° C、216° D、217°8. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、214° B、215° C、216° D、217°8. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、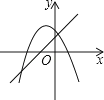 B、
B、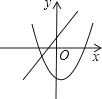 C、
C、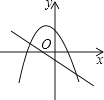 D、
D、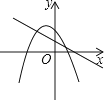 9. 如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( )
9. 如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( ) A、 B、 C、 D、10. 如图, 是边长为1的等边三角形,D、E为线段AC上两动点,且 ,过点D、E分别作AB、BC的平行线相交于点F , 分别交BC、AB于点H、G . 现有以下结论:① ;②当点D与点C重合时, ;③ ;④当 时,四边形BHFG为菱形,其中正确结论为( )
A、 B、 C、 D、10. 如图, 是边长为1的等边三角形,D、E为线段AC上两动点,且 ,过点D、E分别作AB、BC的平行线相交于点F , 分别交BC、AB于点H、G . 现有以下结论:① ;②当点D与点C重合时, ;③ ;④当 时,四边形BHFG为菱形,其中正确结论为( )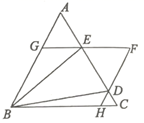 A、①②③ B、①②④ C、①②③④ D、②③④
A、①②③ B、①②④ C、①②③④ D、②③④二、填空题
-
11. 2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7206万人.7206万用科学记数法表示 .12. 因式分解: .13. 如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为岁.
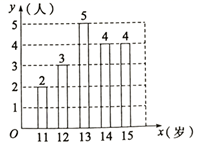 14. 不等式组 的解集是 .15. 如图,在 中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F , 若 , , ,则扇形BEF的面积为 .
14. 不等式组 的解集是 .15. 如图,在 中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F , 若 , , ,则扇形BEF的面积为 . 16. 某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程为 .17. 如图,正方形纸片ABCD的边长为12,点F是AD上一点,将 沿CF折叠,点D落在点G处,连接DG并延长交AB于点E . 若 ,则GE的长为 .
16. 某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程为 .17. 如图,正方形纸片ABCD的边长为12,点F是AD上一点,将 沿CF折叠,点D落在点G处,连接DG并延长交AB于点E . 若 ,则GE的长为 . 18. 如图,正方形 中, ,AB与直线l所夹锐角为 ,延长 交直线l于点 ,作正方形 ,延长 交直线l于点 ,作正方形 ,延长 交直线l于点 ,作正方形 ,…,依此规律,则线段 .
18. 如图,正方形 中, ,AB与直线l所夹锐角为 ,延长 交直线l于点 ,作正方形 ,延长 交直线l于点 ,作正方形 ,延长 交直线l于点 ,作正方形 ,…,依此规律,则线段 .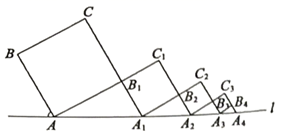
三、解答题
-
19.(1)、计算: .(2)、化简求值: ,其中 .20. 为庆祝建党100周年,让同学们进一步了解中国科技的快速发展,东营市某中学九(1)班团支部组织了一次手抄报比赛.该班每位同学从A . “北斗卫星”;B . “5G时代”;C . “东风快递”;D . “智轨快运”四个主题中任选一个自己喜欢的主题.统计同学们所选主题的频数,绘制成以下不完整的统计图,请根据统计图中的信息解答下列问题:

 (1)、九(1)班共有名学生;(2)、补全折线统计图;(3)、D所对应扇形圆心角的大小为;(4)、小明和小丽从A、B、C、D四个主题中任选一个主题,请用列表或画树状图的方法求出他们选择相同主题的概率.21. 如图,以等边三角形ABC的BC边为直径画圆,交AC于点D , 于点F , 连接OF , 且 .
(1)、九(1)班共有名学生;(2)、补全折线统计图;(3)、D所对应扇形圆心角的大小为;(4)、小明和小丽从A、B、C、D四个主题中任选一个主题,请用列表或画树状图的方法求出他们选择相同主题的概率.21. 如图,以等边三角形ABC的BC边为直径画圆,交AC于点D , 于点F , 连接OF , 且 .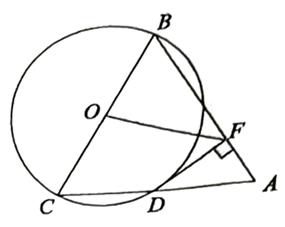 (1)、求证:DF是 的切线;(2)、求线段OF的长度.22. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水箱亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.(1)、如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)、按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.23. 如图所示,直线 与双曲线 交于A、B两点,已知点B的纵坐标为 ,直线AB与x轴交于点C , 与y轴交于点 , , .
(1)、求证:DF是 的切线;(2)、求线段OF的长度.22. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水箱亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.(1)、如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)、按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.23. 如图所示,直线 与双曲线 交于A、B两点,已知点B的纵坐标为 ,直线AB与x轴交于点C , 与y轴交于点 , , .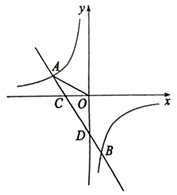 (1)、求直线AB的解析式;(2)、若点P是第二象限内反比例函数图象上的一点, 的面积是 的面积的2倍,求点P的坐标;(3)、直接写出不等式 的解集.24. 如图,抛物线 与x轴交于A、B两点,与y轴交于点C , 直线 过B、C两点,连接AC .
(1)、求直线AB的解析式;(2)、若点P是第二象限内反比例函数图象上的一点, 的面积是 的面积的2倍,求点P的坐标;(3)、直接写出不等式 的解集.24. 如图,抛物线 与x轴交于A、B两点,与y轴交于点C , 直线 过B、C两点,连接AC .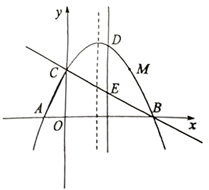 (1)、求抛物线的解析式;(2)、求证: ;(3)、点 是抛物线上的一点,点D为抛物线上位于直线BC上方的一点,过点D作 轴交直线BC于点E , 点P为抛物线对称轴上一动点,当线段DE的长度最大时,求 的最小值.25. 已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D . 我们定义垂足与中点之间的距离为“足中距”.
(1)、求抛物线的解析式;(2)、求证: ;(3)、点 是抛物线上的一点,点D为抛物线上位于直线BC上方的一点,过点D作 轴交直线BC于点E , 点P为抛物线对称轴上一动点,当线段DE的长度最大时,求 的最小值.25. 已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D . 我们定义垂足与中点之间的距离为“足中距”. (1)、[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 .(2)、[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.(3)、[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
(1)、[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 .(2)、[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.(3)、[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;②若 ,请直接写出线段AC、BD、OC之间的数量关系.