内蒙古包头市、巴彦淖尔市、乌兰察布市2021年中考数学试卷
试卷更新日期:2021-07-01 类型:中考真卷
一、单选题
-
1. 据交通运输部报道,截至2020年底,全国共有城市新能源公交车46.61万辆,位居全球第一.将46.61万用科学记数法表示为 ,则n等于( )A、6 B、5 C、4 D、32. 下列运算结果中,绝对值最大的是( )A、 B、 C、 D、3. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或34. 柜子里有两双不同的鞋,如果从中随机地取出2只,那么取出的鞋是同一双的概率为( )A、 B、 C、 D、5. 如图,在 中, , , ,以点A为圆心,AC的长为半径画弧,交AB于点D , 交AC于点C , 以点B为圆心,AC的长为半径画弧,交AB于点E , 交BC于点F , 则图中阴影部分的面积为( )
 A、 B、 C、 D、6. 若 ,则代数式 的值为( )A、7 B、4 C、3 D、7. 定义新运算“ ”,规定: .若关于x的不等式 的解集为 ,则m的值是( )A、 B、 C、1 D、28. 如图,直线 ,直线 交 于点A , 交 于点B , 过点B的直线 交 于点C . 若 , ,则 等于( )
A、 B、 C、 D、6. 若 ,则代数式 的值为( )A、7 B、4 C、3 D、7. 定义新运算“ ”,规定: .若关于x的不等式 的解集为 ,则m的值是( )A、 B、 C、1 D、28. 如图,直线 ,直线 交 于点A , 交 于点B , 过点B的直线 交 于点C . 若 , ,则 等于( ) A、 B、 C、 D、9. 下列命题正确的是( )A、在函数 中,当 时,y随x的增大而减小 B、若 ,则 C、垂直于半径的直线是圆的切线 D、各边相等的圆内接四边形是正方形10. 已知二次函数 的图象经过第一象限的点 ,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 如图,在 中, , 和 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 ,垂足为C , 与AD相交于点E . 若 , ,则 的值为( )
A、 B、 C、 D、9. 下列命题正确的是( )A、在函数 中,当 时,y随x的增大而减小 B、若 ,则 C、垂直于半径的直线是圆的切线 D、各边相等的圆内接四边形是正方形10. 已知二次函数 的图象经过第一象限的点 ,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 如图,在 中, , 和 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 ,垂足为C , 与AD相交于点E . 若 , ,则 的值为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,矩形OABC的OA边在x轴的正半轴上,OC边在y轴的正半轴上,点B的坐标为(4,2),反比例函数 的图象与BC交于点D , 与对角线OB交于点E , 与AB交于点F , 连接OD , DE , EF , DF . 下列结论:① ;② ;③ ;④ .其中正确的结论有( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,矩形OABC的OA边在x轴的正半轴上,OC边在y轴的正半轴上,点B的坐标为(4,2),反比例函数 的图象与BC交于点D , 与对角线OB交于点E , 与AB交于点F , 连接OD , DE , EF , DF . 下列结论:① ;② ;③ ;④ .其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 因式分解: .14. 化简: .15. 一个正数a的两个平方根是 和 ,则 的立方根为 .16. 某人5次射击命中的环数分别为5,10,7,x , 10,若这组数据的中位数为8,则这组数据的方差为 .17. 如图,在 中, ,过点B作 ,垂足为B , 且 ,连接CD , 与AB相交于点M , 过点M作 ,垂足为N . 若 ,则MN的长为 .
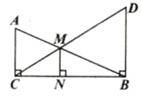 18. 如图,在 中, ,以AD为直径的 与BC相切于点E , 连接OC . 若 ,则 的周长为 .
18. 如图,在 中, ,以AD为直径的 与BC相切于点E , 连接OC . 若 ,则 的周长为 . 19. 如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE , EF , AF . 若 , ,则 的度数为 .
19. 如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE , EF , AF . 若 , ,则 的度数为 .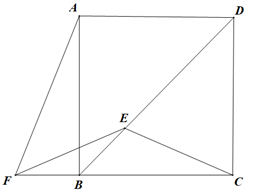 20. 已知抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C , 点 在抛物线上,E是该抛物线对称轴上一动点.当 的值最小时, 的面积为 .
20. 已知抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C , 点 在抛物线上,E是该抛物线对称轴上一动点.当 的值最小时, 的面积为 .三、解答题
-
21. 为了庆祝中国共产党建党100周年,某校开展了学党史知识竞赛.参加知识竞赛的学生分为甲乙两组,每组学生均为20名,赛后根据竞赛成绩得到尚不完整的统计图表(如图),已知竞赛成绩满分为100分,统计表中a , b满足 .
请根据所给信息,解答下列问题:
甲组20名学生竞赛成绩统计表
成绩(分)
70
80
90
100
人数
3
a
b
5
乙组20名学生竞赛成绩统计图
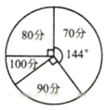 (1)、求统计表中a , b的值;(2)、小明按以下方法计算甲组20名学生竞赛成绩的平均分是: (分).根据所学统计知识判断小明的计算是否符合题意,若不符合题意,请写出正确的算式并计算出结果;(3)、如果依据平均成绩确定竞赛结果,那么竞赛成绩较好的是哪个组?请说明理由.22. 某工程队准备从A到B修建一条隧道,测量员在直线AB的同一侧选定C , D两个观测点,如图,测得AC长为 ,CD长为 ,BD长为 , , (A、B、C、D在同一水平面内).
(1)、求统计表中a , b的值;(2)、小明按以下方法计算甲组20名学生竞赛成绩的平均分是: (分).根据所学统计知识判断小明的计算是否符合题意,若不符合题意,请写出正确的算式并计算出结果;(3)、如果依据平均成绩确定竞赛结果,那么竞赛成绩较好的是哪个组?请说明理由.22. 某工程队准备从A到B修建一条隧道,测量员在直线AB的同一侧选定C , D两个观测点,如图,测得AC长为 ,CD长为 ,BD长为 , , (A、B、C、D在同一水平面内). (1)、求A、D两点之间的距离:(2)、求隧道AB的长度.23. 小刚家到学校的距离是1800米.某天早上,小刚到学校后发现作业本忘在家中,此时离上课还有20分钟,于是他立即按原路跑步回家,拿到作业本后骑自行车按原路返回学校.已知小刚骑自行车时间比跑步时间少用了4.5分钟,且骑自行车的平均速度是跑步的平均速度的1.6倍.(1)、求小刚跑步的平均速度;(2)、如果小刚在家取作业本和取自行车共用了3分钟,他能否在上课前赶回学校?请说明理由.24. 如图,在锐角三角形ABC中,AD是BC边上的高,以AD为直径的 交AB于点E , 交AC于点F , 过点F作 ,垂足为H , 交 于点G , 交AD于点M , 连接AG , DE , DF .
(1)、求A、D两点之间的距离:(2)、求隧道AB的长度.23. 小刚家到学校的距离是1800米.某天早上,小刚到学校后发现作业本忘在家中,此时离上课还有20分钟,于是他立即按原路跑步回家,拿到作业本后骑自行车按原路返回学校.已知小刚骑自行车时间比跑步时间少用了4.5分钟,且骑自行车的平均速度是跑步的平均速度的1.6倍.(1)、求小刚跑步的平均速度;(2)、如果小刚在家取作业本和取自行车共用了3分钟,他能否在上课前赶回学校?请说明理由.24. 如图,在锐角三角形ABC中,AD是BC边上的高,以AD为直径的 交AB于点E , 交AC于点F , 过点F作 ,垂足为H , 交 于点G , 交AD于点M , 连接AG , DE , DF . (1)、求证: ;(2)、若 , , ,求HF的长.25. 如图,已知 是等边三角形,P是 内部的一点,连接BP , CP .
(1)、求证: ;(2)、若 , , ,求HF的长.25. 如图,已知 是等边三角形,P是 内部的一点,连接BP , CP .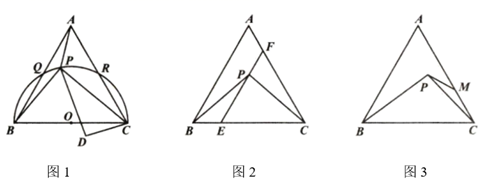 (1)、如图1,以BC为直径的半圆O交AB于点Q , 交AC于点R , 当点P在 上时,连接AP , 在BC边的下方作 , ,连接DP , 求 的度数;(2)、如图2,E是BC边上一点,且 ,当 时,连接EP并延长,交AC于点F . 若 ,求证: ;(3)、如图3,M是AC边上一点,当 时,连接MP . 若 , , , 的面积为 , 的面积为 ,求 的值(用含a的代数式表示).26. 如图,在平面直角坐标系中,抛物线 经过坐标原点,与x轴正半轴交于点A , 点 是抛物线上一动点.
(1)、如图1,以BC为直径的半圆O交AB于点Q , 交AC于点R , 当点P在 上时,连接AP , 在BC边的下方作 , ,连接DP , 求 的度数;(2)、如图2,E是BC边上一点,且 ,当 时,连接EP并延长,交AC于点F . 若 ,求证: ;(3)、如图3,M是AC边上一点,当 时,连接MP . 若 , , , 的面积为 , 的面积为 ,求 的值(用含a的代数式表示).26. 如图,在平面直角坐标系中,抛物线 经过坐标原点,与x轴正半轴交于点A , 点 是抛物线上一动点. (1)、如图1,当 , ,且 时,
(1)、如图1,当 , ,且 时,①求点M的坐标:
②若点 在该抛物线上,连接OM , BM , C是线段BM上一动点(点C与点M , B不重合),过点C作 ,交x轴于点D , 线段OD与MC是否相等?请说明理由;
(2)、如图2,该抛物线的对称轴交x轴于点K , 点 在对称轴上,当 , ,且直线EM交x轴的负半轴于点F时,过点A作x轴的垂线,交直线EM于点N , G为y轴上一点,点G的坐标为 ,连接GF . 若 ,求证:射线FE平分 .