黑龙江省龙东地区(农垦森工)2021年中考数学试卷
试卷更新日期:2021-07-01 类型:中考真卷
一、单选题
-
1. 下列运算中,计算正确的是( )A、 B、 C、 D、2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是由5个小正方体组合成的几何体,则该几何体的主视图是( )
3. 如图是由5个小正方体组合成的几何体,则该几何体的主视图是( )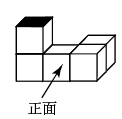 A、
A、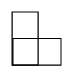 B、
B、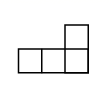 C、
C、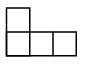 D、
D、 4. 一组数据:3,4,4,4,5,若去掉一个数据4,则下列统计量中发生变化的是( )A、众数 B、中位数 C、平均数 D、方差5. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、96. 已知关于x的分式方程 的解为非负数,则m的取值范围是( )A、 B、 且 C、 D、 且7. 为迎接2022年北京冬奥会,某校开展了以迎冬奥为主题的演讲活动,计划拿出180 元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件15元,乙种奖品每件10元,则购买方案有( )A、5种 B、6种 C、7种 D、8种8. 如图,在平面直角坐标系中,菱形 的边 轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数 的图象同时经过顶点 .若点C的横坐标为5, ,则k的值为( )
4. 一组数据:3,4,4,4,5,若去掉一个数据4,则下列统计量中发生变化的是( )A、众数 B、中位数 C、平均数 D、方差5. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、96. 已知关于x的分式方程 的解为非负数,则m的取值范围是( )A、 B、 且 C、 D、 且7. 为迎接2022年北京冬奥会,某校开展了以迎冬奥为主题的演讲活动,计划拿出180 元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件15元,乙种奖品每件10元,则购买方案有( )A、5种 B、6种 C、7种 D、8种8. 如图,在平面直角坐标系中,菱形 的边 轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数 的图象同时经过顶点 .若点C的横坐标为5, ,则k的值为( )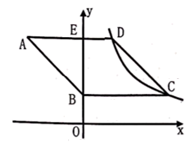 A、 B、 C、 D、9. 如图,平行四边形 的对角线 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )
A、 B、 C、 D、9. 如图,平行四边形 的对角线 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )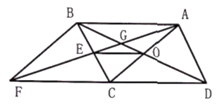 A、4 B、5 C、2 D、310. 如图,在正方形 中,对角线 与 相交于点O,点E在 的延长线上,连接 ,点F是 的中点,连接 交 于点G,连接 ,若 , .则下列结论:① ;② ;③ ;④ ;⑤点D到CF的距离为 .其中正确的结论是( )
A、4 B、5 C、2 D、310. 如图,在正方形 中,对角线 与 相交于点O,点E在 的延长线上,连接 ,点F是 的中点,连接 交 于点G,连接 ,若 , .则下列结论:① ;② ;③ ;④ ;⑤点D到CF的距离为 .其中正确的结论是( )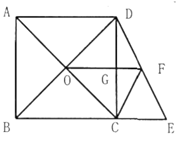 A、①②③④ B、①③④⑤ C、①②③⑤ D、①②④⑤
A、①②③④ B、①③④⑤ C、①②③⑤ D、①②④⑤二、填空题
-
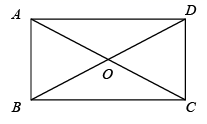
11. 截止到2020年7月底,中国铁路营业里程达到 万公里,位居世界第二.将数据 万用科学记数法表示为 .12. 在函数y= 中,自变量x的取值范围是13. 如图,在矩形 中,对角线 相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使矩形 是正方形.
 14. 一个不透明的口袋中装有标号为1、2、3的三个小球,这些小球除标号外完全相同,随机摸出1个小球,然后把小球重新放回口袋并摇匀,再随机摸出1个小球,那么两次摸出小球上的数字之和是奇数的概率是 .15. 关于x的一元一次不等式组 有解,则a的取值范围是 .16. 如图,在 中, 是直径,弦 的长为5cm,点D在圆上,且 ,则 的半径为 .
14. 一个不透明的口袋中装有标号为1、2、3的三个小球,这些小球除标号外完全相同,随机摸出1个小球,然后把小球重新放回口袋并摇匀,再随机摸出1个小球,那么两次摸出小球上的数字之和是奇数的概率是 .15. 关于x的一元一次不等式组 有解,则a的取值范围是 .16. 如图,在 中, 是直径,弦 的长为5cm,点D在圆上,且 ,则 的半径为 .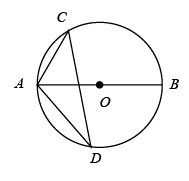 17. 若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为 ,则这个圆锥的母线长为 cm.18. 如图,在 中, , , ,以点O为圆心,3为半径的 ,与 交于点C,过点C作 交 于点D,点P是边 上的动点,则 的最小值为 .
17. 若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为 ,则这个圆锥的母线长为 cm.18. 如图,在 中, , , ,以点O为圆心,3为半径的 ,与 交于点C,过点C作 交 于点D,点P是边 上的动点,则 的最小值为 .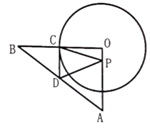 19. 在矩形 中, 2cm,将矩形 沿某直线折叠,使点B与点D重合,折痕与直线 交于点E,且 3cm,则矩形 的面积为cm2 .20. 如图,菱形 中, , ,延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ;再延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ……按此规律,得到 ,记 的面积为 , 的面积为 …… 的面积为 ,则 .
19. 在矩形 中, 2cm,将矩形 沿某直线折叠,使点B与点D重合,折痕与直线 交于点E,且 3cm,则矩形 的面积为cm2 .20. 如图,菱形 中, , ,延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ;再延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ……按此规律,得到 ,记 的面积为 , 的面积为 …… 的面积为 ,则 .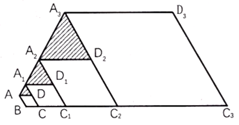
三、解答题
-
21. 先化简,再求值: ,其中 .22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, 的三个顶点分别为 .
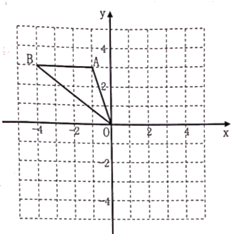 (1)、画出 关于x轴对称的 ,并写出点 的坐标;(2)、画出 绕点O顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求点B旋转到点 所经过的路径长(结果保留 ).23. 如图,抛物线 与x轴交于点 和点 ,与y轴交于点C,连接 ,与抛物线的对称轴交于点E,顶点为点D.
(1)、画出 关于x轴对称的 ,并写出点 的坐标;(2)、画出 绕点O顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求点B旋转到点 所经过的路径长(结果保留 ).23. 如图,抛物线 与x轴交于点 和点 ,与y轴交于点C,连接 ,与抛物线的对称轴交于点E,顶点为点D. (1)、求抛物线的解析式;(2)、求 的面积.24. 为庆祝中国共产党建党100周年,某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛,现随机抽取部分学生的成绩分成A、B、C、D、E五个等级进行统计,并绘制成如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)、求抛物线的解析式;(2)、求 的面积.24. 为庆祝中国共产党建党100周年,某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛,现随机抽取部分学生的成绩分成A、B、C、D、E五个等级进行统计,并绘制成如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题: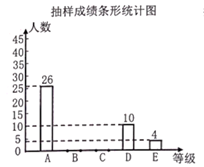
 (1)、本次调查中共抽取学生;(2)、补全条形统计图;(3)、在扇形统计图中,求B等级所对应的扇形圆心角的度数;(4)、若该校有1200名学生参加此次竞赛,估计这次竞赛成绩为A和B等级的学生共有多少名?25. 一辆货车从甲地到乙地,一辆轿车从乙地到甲地,两车沿同一条公路分别从甲、乙两地同时出发,匀速行驶.已知轿车比货车每小时多行驶20km.两车相遇后休息一段时间,再同时继续行驶.两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示的折线 ,结合图象回答下列问题:
(1)、本次调查中共抽取学生;(2)、补全条形统计图;(3)、在扇形统计图中,求B等级所对应的扇形圆心角的度数;(4)、若该校有1200名学生参加此次竞赛,估计这次竞赛成绩为A和B等级的学生共有多少名?25. 一辆货车从甲地到乙地,一辆轿车从乙地到甲地,两车沿同一条公路分别从甲、乙两地同时出发,匀速行驶.已知轿车比货车每小时多行驶20km.两车相遇后休息一段时间,再同时继续行驶.两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示的折线 ,结合图象回答下列问题: (1)、甲、乙两地之间的距离是km;(2)、求两车的速度分别是多少km/h?(3)、求线段 的函数关系式.直接写出货车出发多长时间,与轿车相距20km?26. 在等腰 中, , 是直角三角形, , ,连接 ,点F是 的中点,连接 .
(1)、甲、乙两地之间的距离是km;(2)、求两车的速度分别是多少km/h?(3)、求线段 的函数关系式.直接写出货车出发多长时间,与轿车相距20km?26. 在等腰 中, , 是直角三角形, , ,连接 ,点F是 的中点,连接 .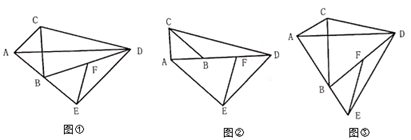 (1)、当 ,点B在边 上时,如图①所示,求证: .(2)、当 ,把 绕点A逆时针旋转,顶点B落在边AD上时,如图②所示,当 ,点B在边AE上时,如图③所示,猜想图②、图③中线段 和 又有怎样的数量关系?请直接写出你的猜想,不需证明.27. “中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入一笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元.(1)、求购进1件甲种农机具和1件乙种农机具各需多少万元?(2)、若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少?28. 如图,在平面直角坐标系中, 的边 在x轴上, ,且线段 的长是方程 的根,过点B作 轴,垂足为E, ,动点M以每秒1个单位长度的速度,从点A出发,沿线段 向点B运动,到达点B停止.过点M作x轴的垂线,垂足为D,以 为边作正方形 ,点C在线段 上,设正方形 与 重叠部分的面积为S,点M的运动时间为 秒.
(1)、当 ,点B在边 上时,如图①所示,求证: .(2)、当 ,把 绕点A逆时针旋转,顶点B落在边AD上时,如图②所示,当 ,点B在边AE上时,如图③所示,猜想图②、图③中线段 和 又有怎样的数量关系?请直接写出你的猜想,不需证明.27. “中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入一笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元.(1)、求购进1件甲种农机具和1件乙种农机具各需多少万元?(2)、若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少?28. 如图,在平面直角坐标系中, 的边 在x轴上, ,且线段 的长是方程 的根,过点B作 轴,垂足为E, ,动点M以每秒1个单位长度的速度,从点A出发,沿线段 向点B运动,到达点B停止.过点M作x轴的垂线,垂足为D,以 为边作正方形 ,点C在线段 上,设正方形 与 重叠部分的面积为S,点M的运动时间为 秒.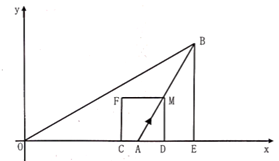 (1)、求点B的坐标;(2)、求S关于t的函数关系式,并写出自变量t的取值范围;(3)、当点F落在线段 上时,坐标平面内是否存在一点P,使以 为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求点B的坐标;(2)、求S关于t的函数关系式,并写出自变量t的取值范围;(3)、当点F落在线段 上时,坐标平面内是否存在一点P,使以 为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.