安徽省滁州市定远县2020-2021学年八年级上学期数学第三次月考试卷
试卷更新日期:2021-07-01 类型:月考试卷
一、单选题
-
1. 确定平面直角坐标系内点的位置是( )A、一个实数 B、一个整数 C、一对实数 D、有序实数对2. 下列长度的三条线段中,不能组成三角形的是( ).A、2cm,5cm,5cm B、3cm,4cm,5cm C、2cm,4cm,6cm D、1cm, cm, cm3. 已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为( )A、100° B、120° C、140° D、160°4. 某复印店复印收费y(元)与复印面数x(面)的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费( )
 A、0.2元 B、0.4元 C、0.45元 D、0.5元5. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( )
A、0.2元 B、0.4元 C、0.45元 D、0.5元5. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( ) A、 B、 C、 D、6. 如图,点 , , , 在同一条直线上, , , , , ,则 的长为( )
A、 B、 C、 D、6. 如图,点 , , , 在同一条直线上, , , , , ,则 的长为( ) A、2 B、4 C、4.5 D、37. 如图,已知 ,添加一个条件使 ,下列添加的条件不能使 的是( )
A、2 B、4 C、4.5 D、37. 如图,已知 ,添加一个条件使 ,下列添加的条件不能使 的是( ) A、 B、 C、 D、8. 若直线y=kx+b经过第一、二、四象限,则函数y=bx-k的大致图像是( )A、
A、 B、 C、 D、8. 若直线y=kx+b经过第一、二、四象限,则函数y=bx-k的大致图像是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
9. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )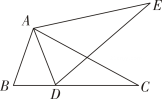 A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED10.
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、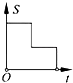 B、
B、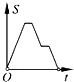 C、
C、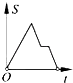 D、
D、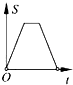
二、填空题
-
11. 在平面直角坐标系中,若将点 向右平移4个单位长度得到点 ,则点B的坐标是 .12. 一次函数 ( 为常数), 随 的增大而增大,则 的取值范围是 .13. 命题“如果 ,那么 ”,是(选填“真”或“假”)命题.14. 如图,在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是.

三、解答题
-
15. 已知点 在 轴上,求 的值以及点 的坐标.16. 已知直线 与直线 的交点横坐标为2,求 的值和交点纵坐标.17. 在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.18. 一次演习中,红军与蓝军在河边激战,蓝军在河北岸Q处,如图,因不知河宽,红军很难瞄准蓝军,聪明的红军指挥官站在南岸O处调整好自己的帽子,使视线恰好擦过帽舌边沿看到蓝军兵营Q处,然后后退到B点,这时他的视点恰好能落在O处,于是他下令测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰蓝军兵营,红军能命中吗?说明理由.
 19. 如图所示, , , 三点在同一直线上,且 .
19. 如图所示, , , 三点在同一直线上,且 . (1)、求证: ;(2)、当 满足什么条件时, ?20. 深秋季节,由于冷空气的入侵,地面气温急剧下降到 以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.某种植物在气温 以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.如图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化的情况,其中0时~5时、5时~8时的图象分别满足一次函数关系.请你根据图中信息,完成下列任务:
(1)、求证: ;(2)、当 满足什么条件时, ?20. 深秋季节,由于冷空气的入侵,地面气温急剧下降到 以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.某种植物在气温 以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.如图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化的情况,其中0时~5时、5时~8时的图象分别满足一次函数关系.请你根据图中信息,完成下列任务: (1)、试求直线 的解析式;(2)、针对这种天气,请判断是否需要对植物采取防霜冻措施,并说明理由.21. 如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一直线上.
(1)、试求直线 的解析式;(2)、针对这种天气,请判断是否需要对植物采取防霜冻措施,并说明理由.21. 如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一直线上. (1)、求证:△BAD≌△CAE;(2)、猜想BD,CE有何特殊位置关系,并说明理由.22. 2020年新冠病毒暴发后,武汉市和黄冈市急需呼吸机,经调查,周边城市合肥市库存12台呼吸机,南昌市库存6台呼吸机.上级决定从上述两市调拨,安排如下:支援武汉市10台呼吸机、黄冈市8台呼吸机.已知从合肥市调运一台呼吸机到武汉市和黄冈市的运费分别是800元和600元,从南昌市调运一台呼吸机到武汉市和黄冈市的运费分别是600元和500元.(1)、设合肥市运往武汉市呼吸机 台,求总运费 (元)关于 的函数关系式;(2)、求出总运费最低的调运方案,最低运费是多少?23. 阅读下面材料:
(1)、求证:△BAD≌△CAE;(2)、猜想BD,CE有何特殊位置关系,并说明理由.22. 2020年新冠病毒暴发后,武汉市和黄冈市急需呼吸机,经调查,周边城市合肥市库存12台呼吸机,南昌市库存6台呼吸机.上级决定从上述两市调拨,安排如下:支援武汉市10台呼吸机、黄冈市8台呼吸机.已知从合肥市调运一台呼吸机到武汉市和黄冈市的运费分别是800元和600元,从南昌市调运一台呼吸机到武汉市和黄冈市的运费分别是600元和500元.(1)、设合肥市运往武汉市呼吸机 台,求总运费 (元)关于 的函数关系式;(2)、求出总运费最低的调运方案,最低运费是多少?23. 阅读下面材料:学习了三角形全等的判定方法(即“ ”“ ”“ ”“ ”)和直角三角形全等的判定方法(即“ ”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.小聪将命题用符号语言表示为在 和 中, , , .小聪的探究方法是对 分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当 是直角时,如图1,在 和 中, , , ,根据“ ”定理,可以知道 .
第二种情况:当 是锐角时,如图2, , .
 (1)、在射线 上是否存在点 ,使 ?若存在,请在图中作出这个点,并连接 ;若不存在,请说明理由;(2)、这种情形下, 和 的关系是(选填“全等”“不全等”或“不一定全等”);
(1)、在射线 上是否存在点 ,使 ?若存在,请在图中作出这个点,并连接 ;若不存在,请说明理由;(2)、这种情形下, 和 的关系是(选填“全等”“不全等”或“不一定全等”);第三种情况:当 是钝角时,如图3,在 和 中, , , .
(3)、请判断这种情形下, 和 是否全等,并说明理由.